О прочности соединения составной анизотропной пластины, жестко защемленной по внешним краям

УДК 593.3                                                 

1Moscow Automobile and Road Construction State Technical University (MADI), North Caucasus branch, Lermontov, Russian Federation

Образец для цитирования: Акопян А. Г. О прочности соединения составной анизотропной пластины, жестко защемленной по внешним краям / А. Г. Акопян // Вестник Донского гос. техн. ун-та. — 2019. — Т. 19, №4. — С. 304-309.

Введение. Рассматривается малонапряженное

Поверхность, соединяющая две пластины, вертикальна к срединной плоскости. Такая составная пластина подвержена изгибу под общей поперечной нагрузкой. Окрестность краевого ребра контактной поверхности соединения свободна от внешних сил. Поместим начало цилиндрической системы координат в угловой точке срединной плоскости пластины. На рис. 1 показана плоскость z=0. Принимаем, что главные оси анизотропии совпадают с осями этой цилиндрической системы координат. Толщину пластины обозначим h, а величины в окрестности точки r=0, относящиеся к областям 0≤θ≤α, -h/2≤z≤h/2 и -β≤θ≤0, -h/2≤z≤h/2, отмечаем индексами i=1, 2 соответственно.

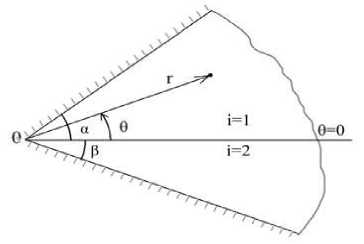
Рис. 1. Схема составной пластины

Материалы и методы. Прогиб w_t каждой области ортотропной пластины в окрестности точки r=0 определяется из уравнения [3]:

• a4wi+Tn   1  84Wl      134"'Ч')П  ia3WtTn   ''            1 ^^9т            1 Э2^4

^L7 ^t "777^ ^{+2 L}7 ^9t ^d7^ ^{+ U ei} 74^9 4 +²^ 7^ ^{-2 L}7 ^9t 7 3 77^ ^{- -U ei} 72^ +^{2( L 9t} + +^^ei) T ⁷^' ^{L ot} 73^7 = ⁰ ,⁽¹⁾ где L_7t, L_9t, L_79t — жесткости каждой области анизотропной пластины:

L7i =---^---h3; Lm =---^---h3; Lr9i = Lrtvet + 2Lkt; LM =^-h

7t    12(1-V71Ve0       yi    12(1-VriV6i)    ’  79t      7t 9t       Kt’ K1

Здесь E_7t, E_9t, v_7t, v_9t, G_t — параметры анизотропии каждой области.

Представляя прогиб пластины в форме wl(r,9)=r^1fl(9 ,Х),(2)

где ft и л — искомые функции и постоянная, из уравнения (1) будет следовать ftm+2(k1tA2 + 1) ft"+(A2 - 1) (k2tA2 - 1)ft =0, к LL79t I        =L7t / где k1t      /L9t, k2t     /L9t .

Корни соответствующего характеристического уравнения для (3) определяются из следующего выражения

H1,2,3,4)t =±J-(k 1t A² + 1) ± M(kl t - k2i)X 2 + 2k 1t + k 2t + 1=±Ч—т               (4)

Механика

Нужно будет рассмотреть три следующих случая:

• 1)    Все четыре корня (4) мнимые (а,>Ь,Ь —величина действительная)

r(1,2,3,4)t = ±^fcti, где случай k=1 соответствует нижнему знаку под радикалом (4), а k=2 — верхнему.

• 2)    Все корни (4) комплексные (b — величина мнимая).

^r(1,2,3,4)i = ± ^(ft ± i ^]i )-

• 3)    Одна пара корней действительная, а другая — мнимая (a< b,b — действительная). ^r(i,2)t = ± ^ft ^{, r}(3A)i = ±b i i.

Для каждого из случаев напишем общее решение уравнения (3):

• 1)    f t =A_t cos o_1t 9+B_t sin to_1t 9+C_t cos to_2t 9+E_t sin co_2t 9

• 2)    f_t =A_t cosh f_t 9 cos] 9 + B_t sinh f_t9 cos]_t 9 + C_t cosh f_t 9 sin]_t9 + +E_t sinh f_t9 sint]_t9 3) f_t =A_t cosh f_t 9+B_t sinh f_t9 + C_t cos]_t 9+E_t sin]_t9,

где At,Bt, Ct,Et — произвольные постоянные.

Тогда для моментов будем иметь

^Mrt = ^—Drt^{r 2 1[}W t" ^{+ (} Л ⁺ 1 ⁾⁽ Л ⁺ v_e t^)ft ]

^Met = ^—Det^{r 2-1 [f}t" ^{+ (} Л ⁺ 1 ⁾⁽ V rt A ⁺ 1 ^)ft ]

Mr6t = —2Dktr2-1f/ перерезывающие силы будут вычисляться по формулам:

^Qrt = ^{-r A-2 [(D}ret ^ ^{— D}et^)ft" ^{+ (Л +} 1 ^)(Drt A^{2 — D}et^)ft ]

Qet = —r2-2 [D6tftm + (Л + 1)(D^ + Det)f/]

Для обобщающей перерезывающей силы будем иметь

Vet = Qet + ^ = -r2-2 (Det ft" + Stft'), где

S t = (Л + 1)D_e t + Л[(Л + 1)D ret + 2(Л - 1)D_kJ.

На контактной поверхности (9 = 0) следует соблюдать условия непрерывности прогиба, угла поворота, изгибающего момента и обобщенной перерезывающей силы .

fi=f2,n=n, Deif"' +Sif1 = Wz^fz,(9)

D ei [f i" + (Л + 1)(т/ г1 Л + 1)f i ] = D e2 [fz' + (Л + 1)(W + 1)f 2 ].

Рассмотрим граничные условия на внешних краях (9 = a, 9 = —р) пластины. В случае жестких заделок ft' = ft = 0,

Подставляя значение ft из (5) в граничные условия (9) и (10), получаем три системы восьми линейных уравнений относительно восьми постоянных At,Bt, Ct,Et для каждого из трех случаев в (5).

Для случая 1:

Ai+ Ci —A2— C2=0(11)

) 11 B 1 +) 21 E 1 —) 12 B 2 —) 22 E 2 =0

• ^Dei< 7 ii^Ai ^{+ D}ei 4 2i^Ci ^{— D}e2 4 i2^A2 ^{— D}e2 4 22^C2 =^{0 O}11^p11 ^B1 + ⁾21 P 21 ^E1 ^{— O}12^p12 ^B2 ^{— O}22^p22 ^E2 = ⁰

A1 cos )11 a+B1 sin o11a+C1 cos )21 a+E1 sin )21 «=0

• A_:)_:1 sin ) ii a B ^On cos ) 11 a+C i ) 21 sin ) 2i a ^Ei )₂ i cos ) 2i a 0

A 2 cos ) 12 р — B 2 sin ) 12 Р +C 2 cos Ш 22 Р — E 2 sin 0 22 P=0

A 2 ) i2 sin 0 12 р + B 2 ) i2 cos 0 12 р +C 2 ) 22 sin CO22 P + E 2 ) 22 cos ) 22 P=0

Здесь использованы следующие обозначения:

_Pj t =( Л + 1 — o² t ) D et +Л[(Л + 1)D ret + 2(Л — 1)D_k t ] 4 it = ⁽ Л + 1 ⁾⁽ УнЛ + 1)-w 2 , j=1, 2

Для случая 2:

A i —A 2 = 0, f i B i + ] i C i — ^B 2 — ] 2 C 2 = 0                              (12)

O i D ei A i + 2D ei f i P i E i — 0)2^2/ 1 2 — 2D e2 ^ 2 ] 2 E 2 = 0

P i ^B1 +q i^C1 ^— P 2 ^B2 ^— ^ 2^C2 =⁰

A1 cosh ^ « cos ]1« + B1 sinh ^a cos ]1« + C1 cosh ^ «sin ]1 к +E1 sinh ^ a sin ]1 к = 0

A1 (f1sinh f1 a cos ]1 a — ]1 cosh f1 a sin ]1a)

+B1 (cosh f1a cos ]1 a — ]1 sinh f1 a sin ]1 a)

+C₁ (^sinh ^ asin ]₁ a + ]₁ cosh ^ a cos ]₁ a +E₁ (f₁cosh f₁ a sin ]₁ a + ]₁ sinh f₁ a cos ]₁ a) = 0 A₂ cosh f₂ Р cos]₂ Р — B₂ sinh ^₂Р cos]₂ Р — C₂ cosh f₂ Р sin■r]₂P+E₂ sinh ^₂Р sin■r]₂P = 0

A 2 (f 2 sinh f 2 Р cos Г 2 Р — Г 2 cosh ^ 2 Р sin Г 2 Р)

• -B 2 (f 2 cosh f 2 P cos 1 2 P -1 2 sinh ^P sin 1 2 P)

• - C 2 (f 2 sinh f 2 P sin1 2 P+1 2 cosh^ 2 P cos 1 2 P) + E 2 (f 2 cosh f 2 P sin1 2 P + 1 2 sinh^Pcos^ P)

= 0, где обозначены toi = f2 -i2 + (A + 1)(vriA + 1)

P i =f i {( f i ² — 31 2 + Я + 1) D_ei +Я[(Я + 1)D_r6i + 2(Я - 1)D ki ]}

Q i = 1 i {(3f i ² - 1 2 + Я + 1)D₆ i + Я[(Я + 1)D_r6 i + 2(Я - 1)D_k i ]}

Для случая 3:

A+ С 1 -Л₂-C 2 =0                                    (13)

f 1 B 1 + 1^ - f 2 B 2 - 1 2 ^ 2 = 0

«АЛ - b1DeiC1 - a2De242 + b2D62C2 = 0 f1P1 B1 - 11Q1E1 - f2p2 B2 + 12Q2E2=0 41 cosh f1 a + B1 sinh f1a + C1 cos 11 к +E1 sin 11 к = 0 41f1 sinh f1 a + B1f1 cosh f1a - C111 sin 11 к +E111 cos 11 к = 0 .2 cosh f2P - B2 sinh f2P + C2 cos 12P - E2 sin 12P = 0 .2f2 sinh f2P - B2f2 cosh f2P - C212 sin 12P - E212 cos 12 P = 0, где di = f2 +(X+1)(vr< + 1) , bi = 12 - (Я + 1)(vH + 1)

P i =( f i ² +Я + 1) D₆ i +Я[(Я + 1)D r ₆ i + 2(Я - 1)D_k i ]

^Qi = ^{(1 - Я - 1)D}ei ^{- Я[(Я + 1)D}r6i ^{+ 2(Я - 1)D}ki^]

Для существования нетривиального решения однородных систем (11), (12) и (13) линейных алгебраических уравнений относительно коэффициентов 4i,Bi,Ci,Ei необходимо, чтобы определители этих систем равнялись нулю

A(^a,P,V ri ,v₆ i ,E ri ,E₆ i ,G i )=0                                       (14)

Из (2) и (6) следует, что если 0< ReЯ1 <1 , то при приближении к краю поверхности соединения (г^ 0) напряжения (моменты) неограниченно возрастают, при этом порядок особенности равен | ReЯ1 -1| . А если ReЯ1 > 1 , напряжения убывают до нуля при приближении к вершине угла.

Результаты исследования. Таким образом, исследование характера напряженного состояния в окрестности ребра края поверхности соединения составной анизотропной пластины при изгибе приводится к отысканию корня Я трансцендентного уравнения (14) с наименьшей положительной частью для фиксированных углов и механических характеристик соединяемых материалов.

Приравнивая нулю определители этих новых систем, получаем уравнения относительно Я для каждого из трех случаев соответственно. Проведено численное решение этих уравнений для следующих групп параметров:

• 1)    у = 1,G i = ^; 2)у = 1,G i = 4p i ; 3) у = 1,G i = P i /4;

• 4)    у = 1/2, G i = P i ; 5) у = 1/2 ,G i = 4p i ; 6) у = 2, G i = 4p i .

В численных расчетах везде учтено замечание Фойгта [6] о равенстве Eri = Eei.

Некоторые результаты численного исследования корня Я, в зависимости от угла <р =к +P, приведены в таблице где к= 10⁰.

Таблица 1

Значения параметра Я в зависимости от углов к и P

ф	1	2	3	4	5	6
140	1,533	0,845	2,34	1,574	0,784	0,88
160	1,288	0,703	1,72	1,146	0,653	0,73
180	1,000	0,596	1,51	0,910	0,556	0,61
200	0,816	0,516	1,039	0,756	0,485	0,53
230	0,652	0,436	0,817	0,614	0,416	0,447
290	0,519	0,373	0,60	0,508	0,367	0,375
360	0,500	0,325	0,563	0,474	0,311	0,333

Механика

Таблица показывает, что для данных углов, в зависимости от параметров анизотропии, может быть концентрация напряжений в вершине или не быть.

Можем решить и обратную задачу [1–5]. Построим кривые, которые при фиксированных значениях механических характеристик материалов на плоскости к /? разделяют области конечных и бесконечных напряжений (моментов). Предполагая, что вблизи границы области высокой концентрации напряжений наименьший корень уравнения (11) действительный, положим в этом уравнении Л =1 (предварительно освобождаясь от двукратного корня Л =1 ) и найдем наименьшие положительные значения углов к и /? в зависимости от параметров анизотропии. Геометрические места этих точек в плоскости к /? образуют те предельные кривые, которые разделяют концентрационную область (выше кривых) от областей малонапряженности (ниже кривых). Численная реализация полученного уравнения позволяет в пространстве параметров a, P,v_rbv_6l, E_rl, E_6l, G_t определить зону малонапряженности для края, обеспечивающую прочность соединения.

На рис. 2 показаны эти кривые для различных значений параметров анизотропии. Линии 1-9 отвечают следующим параметрам: 1) у = 1, G , = н; 2) у = 1^, G , = н; 3) у = 2, G , = н; 4) у = 1, G , = 4^;

• 5)    У = 1/2, G i = 4щ ; 6) у = 2, G , = щ; 7) у = 1, G , = щ/4; 8) у = 1/2, G , = щ/4 ; 9) у = 2, G , = щ/4.

  

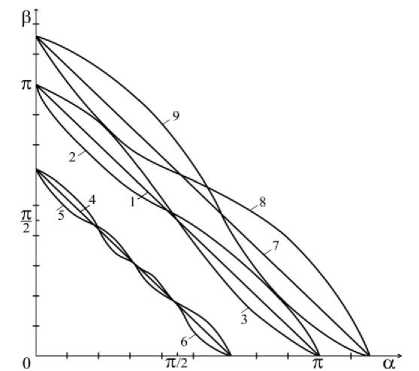
  Рис. 2. Распределение зон малонапряженности

  
  
  
  

На графиках прямые линии соответствуют однородной пластине, а кривые — составной.

Обсуждение и заключения. Если для однородной изотропной пластины с углом раствора больше п всегда имеется концентрация напряжений в вершине, а с углом меньше п отсутствует, то для однородной анизотропной пластины, а также составной изотропной и анизотропной пластин, как показывают графики на рис. 2, эта закономерность нарушается.

Видно, что степень концентрации перерезывающих сил вблизи угловой точки на единицу выше, по сравнению с моментами, что объясняется несовершенством классической теории изгиба пластин.

Аналогичным образом можно рассматривать граничные условия, когда плита свободно оперта по внешним краям, внешние края свободны, а также смешанные краевые условия.

Рассмотренную здесь задачу можно также исследовать, используя уточненную теорию изгиба анизотропных пластин [12, 13], позволяющую уйти от ограничений, налагаемых аппроксимацией Кирхгофа, и сравнить результаты.