О пропускной способности дорожной сети при исследовании транспортных потоков

Одной из актуальных проблем современного населённого пункта является исследование транспортных потоков на автомобильных дорогах. С каждым годом объём перевозок автомобильным транспортом растёт. Проблема дорожного движения уже не первый год стала одной из самых острых для крупных городов по всему миру.

Основной показатель загруженности улиц - средняя скорость движения. Исследования британской компании Keepmoving [4] показали, что с годами резко снижается средняя скорость движения транспортных средств. Причём эта проблема стала затрагивать не только крупнейшие города мира, но и более мелкие.

Управление транспортными потоками на автомобильных дорогах тесно связано с понятием пропускной способности. Можно рассмотреть дорожную сеть, состоящую из отдельных элементов:

• •    простых участков дороги, т.е. участков имеющих один въезд и один выезд, на которых движение происходит от одной точки к другой, и при этом его параметры не меняются на всей длине пути;

• •    перекрёстков, на которых возможно несколько въездов и несколько выездов и движение в нескольких возможных направлениях.

Рассматривая дорожную сеть, состоящую из таких элементов, можно представить её в виде графа [2], носитель которого образуют перекрёстки, сигнатуру — простые участки дороги. Граф является взвешенным. Считаем, что каждое ребро, соответствующее простому участку дороги, взвешено его пропускной способностью.

Для наиболее эффективной работы дорожной сети, необходимо обеспечить возможность прохождения через неё максимального потока. Существуют различные алгоритмы поиска максимального потока через сеть [2,3]. Именно к задаче исследования максимального потока через сеть дорог можно свести задачи, связанные с управлением транспортными потоками, являющиеся базовыми при принятии решений по управлению автомобильными дорогами [1]. Однако, многие алгоритмы работают с пропускными способностями отдельных элементов дорожной сети. Несмотря на это, само понятие «пропускная способность» остаётся не до конца понятным.

С одной стороны, пропускная способность — это количество транспортных средств, проходящее по определённому участку дорожной сети за единицу времени. Для оценок часто используют результаты наблюдений, которые не дают объективного представления, т.к. имеет место динамика пропускной способности [1,4].

С другой стороны, под пропускной способностью можно понимать максимальное количество транспортных средств, находящихся одновременно на участке дороги. Из этого определения, пропускную способность можно найти по формуле:

_ nLi

1 L

m где Si – пропускная способность простого участка дороги, Li – длина участка дороги, n – количество полос, Lm – длина транспортного средства. При таком рассмотрении на дороге умещается максимальное количество транспортных средств (рис. 1).

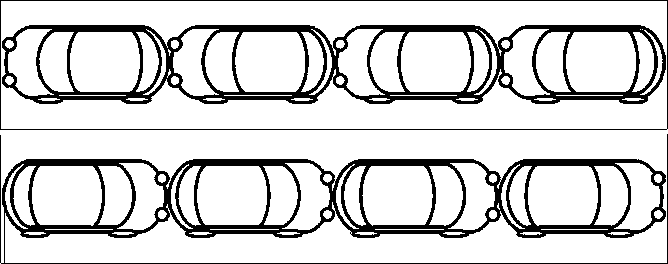
L

m

Рис. 1

Однако, обеспечить безопасную скорость движения (отличную от 0) при таком подходе невозможно. Предполагается, что для безопасного движения по участку дороги, необходимо соблюдать дистанцию между транспортными средствами. Причём, дистанция зависит от скорости транспортного средства. Существуют различные методики оценки зависимости безопасного расстояния между транспортными средствами от их скорости. Эти методики предполагают различные способы получения таких зависимостей – путём расчётов по уравнениям движения автомобиля, путём моделирования, обработки экспертных оценок и т.д.. Будем считать, что рассматриваемая зависимость строится путём интерполирования по нескольким точкам, полученным способами, предложенными выше (рис. 2). Тогда, пропускную способность можно оценить как количество транспортных средств на дороге с учётом безопасного расстояния между ними:

S _ —nLi—1   (Ld (v) + Lm )

где S i – пропускная способность простого участка дороги, L i – длина участка дороги, n – количество полос, L m – длина транспортного средства, L d (v) – длина безопасного расстояния до следующего транспортного средства. При таком рассмотрении на дороге умещается максимальное количество транспортных средств (рис. 3).

В полученной формуле не учтены временные характеристики, поскольку такая организация движения транспортных потоков предполагает, что транспортный поток будет двигаться с требуемой скоростью, а значит за определённое время достигнет пункта назначения.

Также, стоит отметить, что ряд параметров в полученной формуле зависит от особенностей дороги и её окружения, учёт которых позволит более точно оценить пропускную способность элементов дорожной сети [1].

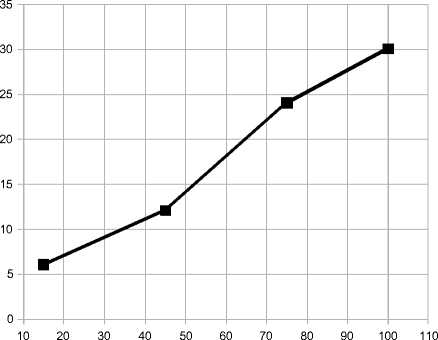
V' км/ч	15	45	75	100
Ld(V)' м	6	12	24	30

Рис. 2

В дальнейшем, оценив пропускную способность каждого участка дороги, можно будет найти максимальный поток через сеть, тем саамам оценив пропускную способность дорожной сети в целом.

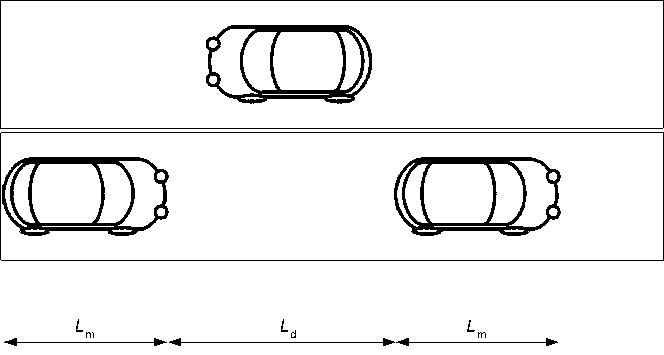
Рис. 3

Результат, полученный при исследовании рассмотренной модели транспортных потоков является лишь одном из этапов принятия решений по управлению транспортными потоками. Корректность полученного решения можно будет в дальнейшем оценить путём имитационного моделирования [1].