О ранжировании критериев выбора решений, сформированных на матрице риска

ВЕСТНИК 2017

Проблема управления соотношением оптимизма и пессимизма является основной для лица, принимающего решение (ЛПР) в задаче выбора стратегий в условиях статистической неопределенности («игра с природой»). Один из подходов к решению этой проблемы состоит в использовании критерия Гурвица [1–4], дающего возможность варьировать значение коэффициента оптимизма в зависимости от специфики задачи выбора стратегии и предпочтений ЛПР по отношению к риску. Однако возможности критерия Гурвица в этом отношении весьма ограничены, поскольку он взвешивает две экстремальные ситуации – наилучшую (критерий максимакса) и наихудшую (критерий Вальда), полностью игнорируя остальные.

Поэтому в большинстве случаев выбор для ЛПР ограничен либо предельно оптимистичным, либо предельно осторожным решением. Однако в ряде случаев при средних значениях коэффициента оптимизма выбор по критерию Гурвица указывает на третью промежуточную альтернативу, которую, как правило, рекомендуют критерии Лапласа и Сэвиджа. В частности в нашей работе [5] анализ случайной выборки из 150 матриц эффективности с размерностью 6х6 и с нормальным распределением двузначных чисел показал, что критерий Гурвица вопреки ожиданиям находит третью (промежуточную) альтернативу в 15% случаев.

Кроме того в [5], а также в [6–7] было показано, что в 22% случаев имеет место совпа-

ВЕСТНИК 2017

дение выбора единственной (оптимальной) альтернативы по критериям Вальда и максимакса, причем на эту альтернативу указывают также критерии среднего оптимизма – Лапласа и Сэвиджа. Тем не менее в основном критерий Гурвица «не чувствует» промежуточных альтернатив, причем в ряде случаев при изменении коэффициента оптимизма в пределах 30–50% одна из двух выбранных альтернатив не изменялась. Это означает, что на практике ЛПР, применяя критерий Гурвица, может в широких пределах варьировать коэффициентом оптимизма, оставаясь при неизменном выборе одной из двух альтернатив.

В этой связи, в работе [8] мы рассмотрели возможность формирования порядковой измер тельной шкалы для априорного выбора оптими ма критериев выбора решений. Для этого был привлечены основные классические критери а также был сформирован ряд дополнительны критериев на матрице риска (потерь). При это коэффициент оптимизма критерия Гурвица и пользовался для задания равномерных градаци формируемой (заведомо неравномерной) шкал

В результате удалось установить относ тельно устойчивые отношения нестрогого порядка для группы из шести критериев, а именно: критериев Вальда, Сэвиджа, произведения Лапласа, максимакса и предложенного нами критерия существенного риска, который занял позицию между критериями Лапласа и максимакса. Однако некоторые дополнительные критерии, сформированные на матрице риска (потерь) по аналогии с классическими критериями, были нами отвергнуты, поскольку проявили весьма слабую степень корреляции со своими классическими аналогами. Тем не менее, представляет интерес оценивание возможности построения дополнительной (альтернативной) ранговой шкалы для измерения риска ЛПР при принятии решения в условиях статистической неопределенности.

Для решения этой задачи рассмотрим сл дующие критерии, сформированные на матри риска: максимакса риска ( К_MR ), существенно риска ( К_R ), усредненного (среднего) риска ( K_AR максимина ( K_Mm ) и хорошо известный минимак ный критерий Сэвиджа ( К_mM ).

Формально новые критерии, сформирова ные на матрице риска, могут быть представлен следующим образом.

Критерий максимакса риска:

КMR = maxi maxj Δxij,(1)

где _Δ x_ij – разность между максимальной и текущей оценками в каждом столбце матрицы риска.

Критерий усредненного риска:

KAR= maxi ( 1 Δxij).(2)

n

Критерий максимина риска:

KMm = maxi minj Δxij .(3)

Критерий существенного риска:

КR = maxi maxj Δyij,(4)

где _Δ y_ij – разность между максимальным и текущим значениями эффективности в каждой строке матрицы эффективности.

Объединим все рассматриваемые критерии на пробной ранговой шкале риска, упорядочив их по мере уменьшения степени их взаимной корреляции с критерием рискового максимакса.

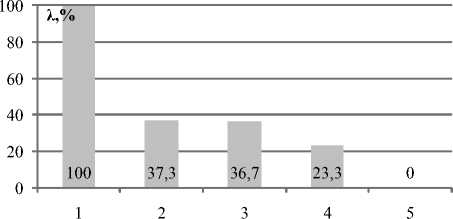
Рис. 1. Коэффициенты взаимной корреляции ( λ _n-MR )

выделенных критериев с критерием максимакса риска (1 – λ MR -MR = 1,0; 2 – λ R -MR = 0,3733; 3 – λ AR -MR = 0,3666;

4 – λ _{Mm -MR} = 0,2333; 5 – λ _{mM -MR} = 0.)

Как видим, имеет место плавное уменьшение значений коэффициентов парной корреляции рассмотренных критериев с критерием рискового максимакса, т.е. между выделенными критериями существует отношение строгого порядка по степени их рискованности:

^KmM ^ ^KMm ^ ^KAR ^ ^KR ^ ^KMR ^. (⁵)

Оценим устойчивость выявленного отношения, ранжируя рассматриваемые критерии по мере убывания коэффициентов их парной корреляции с минимаксным критерием Сэвиджа (рис. 2).

Рис. 2. Коэффициенты взаимной корреляции ( λ _n-MR )

выделенных критериев с критерием минимакса риска

(Сэвиджа) (1 – λ _{mM -mM} = 1,0; 2 – λ _Mm-mM = 0,1533;

3 – λ R -mM = 0,0866; 4 – λ AR -mM = 0,0133; 5 – λ MR -mM = 0)

Серия «Сложные системы: модели, анализ и управление». Выпуск 2

Как видим, отношение строгого порядка степени рискованности критериев полностью не сохраняется: изменилось взаимное положение критериев существенного риска и усредненного риска:

^KmM ^ ^KMm ^ ^KR ^ ^KAR ^ ^KMR ^. (⁶)

Следовательно, можно считать, что между критерием существенного риска К_R и критерием усредненного риска K_AR существует отношение эквивалентности ( К_R ≈ K_AR ).

Сформированная порядковая шкала рисков может в принципе быть использована при выборе решений в условиях риска в качестве вспомогательного инструмента – дополнительно к предложенной в [4] порядковой шкале оптимизма. При этом следует иметь в виду относительную устойчивость отношений порядка рассмотренных нетрадиционных критериев, т.е. учитывать существование между некоторыми из них отношений нестрогого порядка.