О РАСЧЕТЕ АБЕРРАЦИОННЫХ КОЭФФИЦИЕНТОВ ДЛЯ ЦИЛИНДРИЧЕСКОГО ЗЕРКАЛА

корнем функции, стоящей в (1) под знаком радикала

Данная работа является продолжением работ [1–3], посвященных изучению свойств электростатического энергоанализатора типа цилиндрическое зеркало (ЦЗ) (цилиндрический конденсатор) при учете заряженных частиц (в нашем случае это электроны), имеющих азимутальную компоненту скорости.

Ранее подобная тематика рассматривалась в ряде работ [4–7]. В этих работах изучались траектории электронов в цилиндрической системе координат. Наиболее близкой к представленной статье является работа [4]. Нами использовались ее основные обозначения.

Можно выделить три области прохождения траекторий: первое пролетное (дрейфовое) пространство, дисперсионное пространство, второе пролетное пространство. Основную трудность представляет вычисление траекторий в дисперсионном пространстве.

Уравнение движения заряженных частиц (электронов) в дисперсионном пространстве, записанное в цилиндрической системе координат, допускает упрощение, в результате которого получается зависимость времени от радиальной координаты в виде интеграла (в обозначениях работы [3])

I r I sin² 9 — sin² 9 - sin² ф-\ — I k r )

—

Xх k

r

lln -

k

k ri)

= 0.      (2)

T = — х

V 0

r m

XJ

d r

Ir 1 ² 1 sin ² 9 - sin ² 9 - sin ² ф-\ — I —In k r ) k

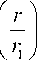
где r_m — величина наибольшего удаления электронов от внутреннего цилиндра, являющаяся

Начальные условия для уравнений движения: r ₀ — радиус точки вылета электронов из источника; V ₀ — скорость электронов до входа в дисперсионное пространство; ( ϑ , ϕ ) — углы в локальной сферической системе координат, привязанной к точке эмиссии r ₀ ; ϑ — угол между нормалью к плоскости XY (осью Z) и вектором скорости; ϕ — азимутальный угол, отсчитываемый вокруг точки r ₀ , между осью Y и проекцией вектора скорости на плоскость XY ( V_xy ); ось Y локальной сферической системы координат совпадает с прямой линией, проведенной из точки пересечения оси Z с плоскостью XY до точки вылета электронов из источника; k = — ( E/U ) In ( r ₂ / r ) ; E — кинетическая энергия электронов до влета в дисперсное пространство; r ₁ , r ₂ — радиусы внутреннего и внешнего электродов ЦЗ; U — потенциал на внешнем электроде ЦЗ; на внутреннем электроде ЦЗ установлен потенциал, равный нулю.

Решение уравнения движения в его преобразованном виде (1) требует решения двух задач: нахождение корня уравнения (2) и собственно решение (интегрирование) уравнения (1). В [3] приведено выражение для наибольшего удаления r_m от внутреннего цилиндра:

r m = r m 0 ^X

x exp <^ — LambertW 2

V

r ²

- ’sin² 9 - sin² ф - -0- r_m 2₀

,

ВЫЧИСЛЕНИЕ ВКЛАДА В АБЕРРАЦИОННЫЕ КОЭФФИЦИЕНТЫ ОТ ДРЕЙФОВЫХ ПРОСТРАНСТВ

где r m о = ' 1 - e^{k -} sin ⁹ — наибольшее удаление электронов от внутреннего цилиндра при ф = 0 , т.е. без азимутальной компоненты скорости, LambertW( x ) — функция Ламберта [8].

Уравнение движения может быть решено разложением редуцированного к виду (1) уравнения движения в ряд Тэйлора. В работе [4] расчет правой части (1) был выполнен с точностью до малой величины порядка tg²( γ ) , где γ — угол, пропорциональный азимутальному углу. С одной стороны, в этом случае нельзя требовать изотропности начального распределения электронов по этому углу. С другой стороны, остается вопрос, достаточно ли разложение до членов порядка tg² ( γ ) для получения приличных по точности результатов. Результаты работы [3] показывают, что в ряде случаев этого приближения может быть недостаточно.

В работе [3] проведено разложение правой части уравнения (1) в ряд Маклорена по переменной x = sin ² ( ф ) до четвертого порядка. Показано, что вплоть до величины угла ϕ в 20° этот подход дает решение уравнения (1) с весьма хорошей точностью. При этом в каждой точке эмиссии рассматривалась (местная) сферическая система координат (СК). Поэтому для этого случая изотропное распределение эмитируемых электронов является обоснованным.

Можно выражение в правой части (1) разложить в двойной ряд (Тэйлора по углу ϑ и Маклорена по углу ϕ ). Коэффициенты в этом ряду являются аберрационными коэффициентами (АК). До настоящего времени считалось невозможным аналитически получить аберрационные коэффициенты для цилиндрического зеркала. Хотя в нескольких работах приведены аналитические выражения для некоторых АК. Так, в [9] приведены выражения для АК по углу ϑ до второго порядка и приведено численное выражение для АК по углу ϑ третьего порядка. В [4] рассмотрен более общий случай с азимутальными траекториями в приближении малости некоторого угла, который при стремлении к нулю сходится к углу ϕ .

Все вычисления в данной работе проведены для ЦЗ с радиусом внутреннего цилиндра ' 1 = 2 см, радиусом внешнего цилиндра r ₂ = 5 см, на внутреннем цилиндре установлено напряжение, равное нулю, на внешнем цилиндре — U = - 100 B.

Ниже все расстояния будем выражать в мм.

В каждом из дрейфовых пространств на заряженную частицу не действует никакая сила, поэтому ее движение является прямолинейным. Описание такого движения является простым и подробно рассмотрено в [3]. Проекции траектории электрона в дрейфовых пространствах на ось Z приведены в [3].

Проекция на ось Z траектории электрона в первом дрейфовом пространстве:

L P ) = ( а' - Г ) ² - sin ² ( ф ) - г , - cos( ф ) ) /tg( 9 ).

Проекция на ось Z траектории электрона во втором дрейфовом пространстве:

L P ) = ( Nr² — r ₀2 - sin²( ф ) - ' 0 - cos( ф ) -

- vPy- r02 - ^2(ф )) /w), где Py — радиус цилиндра, содержащего выходную диафрагму.

Суммарный вклад в проекцию траектории электрона на ось Z от обоих дрейфовых пространств:

L P - = L P - + L P - = ( 2 -77 - ' - Sin 2 ( ф ) -

^- ' 0 ■ С05( ф ) ^- 7 P y ^{1 -} 7 ■ sin ( ф ) ) /tg( ⁹ )-

Введем обозначения s = sin( 9 ₀ ), c = cos( 9 ₀ ).

Суммарный вклад в проекцию траектории электрона на ось Z от обоих дрейфовых пространств будем искать в виде разложения в ряд

L P ) =

= A ^p₀ ) + A (, P) -А ф + A , P ) -A 9 + A ^p ) -А ф -А 9 + ...    (4)

Член разложения правой части выражения (1) порядка ( i _ϕ , j _ϑ ) (с точностью до константы этот член равен производной этого порядка) обозначен как A_i ⁽ _, ^P _j ⁾ .

A 0 P = ^{(2 -} ' 1 - ^r 0 - P y ) ^{- c} / ^s .

A ( ^p ) =

= ^{- r} 0 ^{- (2 - r} 0 ^{- P}y ^{- r} 0 ^- r l ^- r l ^{- P}y ) ^- c /^{(2 -} r l ^{- P}y • ^s )•

( P )                                                               2

A 2,1     ' 0  ⁽² ' 0   P y     ' 0   ' 1      ' 1   P y )/ ^{(2 s} ' 1   P y ^).

( P )

A 2,2 =

= ^- r o ■ (2 ■ r o ■ P y ^- r o ■ r i ^- r i ■ P y ) ■ c /(2 ■ ^{5 3} ■ r i ■ P y ).

A, = - r o ■ (6 ■ P y ³ ■ r o ³ - 8 ■ P y ■ r o ■ r +

2   3    33  33       33

⁺ ^ ¹ y r o r i ^J r o r i ⁺ r i y ) ) cj (^{X 5} r i y ) ).

A o P =- (2 ■ r - P y - r ₀ )/ 5 ².

A o P 2) = ⁽² ■ r i ^{- r} o ^- P y ) ■ c / ^{5 3}.

A P ) =- (2 ■ r i - p y - r o ) ■ (i + 2 ■ c ²)/ (3 ■ 5 ⁴).

A ^P ) = c ■ (2 ■ r i - P y - r o ) ■ (2 + c ²)/(3 ■ 5 5 ).

Отметим, что в силу того, что разложение правой части выражения (1) по переменной ϕ реализуется в окрестности точки ф ₀ = o , по отношению к которой L ^{( P )} симметрична, все нечетные по переменной ϕ вклады в AK равны нулю.

ЧИСЛЕННОЕ НАХОЖДЕНИЕ ВКЛАДА В АБЕРРАЦИОННЫЕ КОЭФФИЦИЕНТЫ ОТ ДИСПЕРСИОННОГО ПРОСТРАНСТВА

В основе метода лежит возможность вычислять ( D )

значения L проекции траектории электрона в дисперсионном пространстве на ось Z (см. работу [3]). Фиксируем некоторое значение угла 9 = 9 _o , для угла ф ₀ выбираем 2 ■ N _ф + i равноотстоящих значений ф _i = ф ₀ + i ■ А ф , i е ( - Ы _ф , Ы _ф ), А ф = i ° и вычисляем на множестве ф _i значения L ⁽ _i ^{D )} . Далее строим интерполяционный полином по переменной ϕ в окрестности точки ϕ ₀ , проходящий через эти точки:

N n

L D Wo) = Е A-»'(» - ф») *■ n =o

Коэффициенты этого полинома равны вкладу в соответствующие аберрационные коэффициенты A_{n ,0} от дисперсионного пространства в окрестности угла ф ₀ и при 9 = 9 _o .

Аналогично проводим вычисление проекции траекторий электрона для фиксированного угла ф = ф ₀ и 2 ■ N ₉ + 1 равноотстоящих значений угла 9 j = 9 _o + j ■А У , А 9 = i°. Строим интерполяционный полином, проходящий через все точки L ^{( D )}( ϕ 0 , ϑ j ):

N ϑ

LD)(фo,9) = £Ao,m ■ (9 - 9o)m . m =o

И получаем значения вклада в соответствующие аберрационные коэффициенты A _{0, m} от дисперсионного пространства в окрестности угла ϑ ₀ и при ф = ф ₀.

Несколько более сложно обстоит ситуация с вычислением "смешанных" аберрационных коэффициентов (вычисление смешанных производных). Для этого вычисляем величину L ^{( D )} на прямоугольном          массиве          точек

^{( i} ф , ^j 9 ) = ^{( - N} Ф - ^N Ф ) ^{X ( -} N 9 - N 9 ), равноотстоящих по углам ф и 9 соответственно, ф _i = ф ₀ + i ■А ф , 9 j = 9 _o + j ■ А 9 , А ф = i ° , А 9 = i°.

Нам        необходимо        вычислить л i    dn ■ mLD )(ф,9) T

An, m =- Г д „ дот - Tk частную произ’     n !■ m! dфn ■ d9m водную от нескольких переменных можно вычислять последовательным дифференцированием в произвольном порядке, то справедливо равенство

A n , m

i dn < i dmL(D)(ф,9) ^ n !•' dфn ^ m!     d9m J i dm < i dnL(D)(ф,9) ^ m! d9m (n!    dфn    J-

Поэтому для вычисления АК порядка ( n ■ m )

можно сперва для всех возможных углов ϕ _n вы- d ^m L ^{( D )} ( ϕ , ϑ )

числить производную mn . Т.е. для каждого ф = фп строим интерполяционный полином в окрестности точки ϑ0 , коэффициент которого с номером n с точностью до равен этой про-m!

изводной. Далее для вычисления производной от полученной величины по переменной ϕ используем ранее описанную методику. Точно такое же действие можно проделать, поменяв порядок нахождения производных.

АНАЛИТИЧЕСКОЕ НАХОЖДЕНИЕ ВКЛАДА В АБЕРРАЦИОННЫЕ КОЭФФИЦИЕНТЫ ОТ ДИСПЕРСИОННОГО ПРОСТРАНСТВА

Основную трудность представляет вычисление вклада в аберрационные коэффициенты от дисперсионного пространства.

Проводим разложение правой части формулы (1) в ряд Тэйлора по углу ϑ и Маклорена по углу ϕ и выделяем коэффициенты этого разложения. Эти коэффициенты и будут искомыми АК. Ниже будем использовать обозначения:

L D ) =

= A 0D ) + A ( D ) • A ^ + A 0 D ) • A S + Ay ) • A p • A S + ..., (5)

( D )

где L определено выше.

Для члена A ₀ ⁽ _, ^D ₀⁾ :

x (2 • e^p / p + V n • erf( p ) • ( - 1 + 2 • c ² • k )).

A0D) = 4k • c • rmo X

x(4• k2 • c2 • s2 -6 • k • 52 + 2 • k • c2 - 1) • 44 • erfp) +

+2* k3/2 • c• rm0 • e-p • (2• k• c2 • s2 -3*s2 + c2)/p-

5/2   3   2           - p ²     3

-2" k • c • s • rm 0 • e p / p .

r m 1

A 0 = 2 • cos( S ₀ ) • J

d r .

7           1     i r sin2(So)--ln -\          k  I r

Проведя в интеграле замену переменной

y ² = k sin²( S ₀ ) - ln

r

V r1 J

, легко получить

4 ( D ) = ² 4k • ^{COs( S} o ) • ^- m o • 44 • er ^f( p ),

A0D) = 4k • s • rmo • (1 - 20 • c2 • k -

• -    24 • s ² • c ² • k ² + 6 • k • s ² + 8 • k ³ • s ² • c ⁴ +

• + 12 • c ⁴ • k ² ) • 44 • erf( p )/3 +

• +    k ^3/2 • s • r_{m 0} • e - ^{p 2} • ( - 20 • c ² - 24 • k • s ² • c ² +

• +    6 • s ² + 8 • k ² • s ² • c ⁴ + 12 • k • c ⁴)/(3 • p ) +

। 1 5/2         2              - p^ /1       2

• +    k • s • c • rm o • e p • (12 • s -

• -    4 • k • s ² • c ² - 6 c ²)/(3 • p ) +

• +    2k7/2 • s = • c* • rm0 • e-p’/p>.

где p = ^k • ^Siⁿ²( ^S o ) , ^- m 0 = ^- 1 • e k • ^S1 n ^{2( S o)}.

Это выражение практически совпадает с тем, что получено в [4]. Отличие только в определении функции erf( p ) . Мы пользовались определением справочника [10].

Для АК A ₀ ⁽ _, ^D ₁⁾ имеем:

Введем для удобства величины L _{1 - 5}

L₁ = c • 4k • r_m 0 • (16 • c ⁴ • k ⁴ • s⁴ + 48 • c ⁴ • k ³ • s² -

- 80 • c ² • k ³ • s ⁴ + 12 • c ⁴ • k ² - 160 • c ² • k ² • s ² +

+ 60 • k ² • s ⁴ - 20 • c ² • k + 60 • k • s ² +

A0 D = -2sin(So) • J'           1           dr + r A sin2(So)- 1ln| - |

N ^k V r J

+ 1) • 44 • erf( p ) / 6 .

где

r_{m 1}

+ 2cos( S ₀ ) • J r ₁

sin( S ₀ ) • cos( S ₀ )

V

,        1 (r sin2(So)--ln -k

3/2

d r +

+

^{2cos( S} 0 ⁾ • ^r m 01

^{Sin (S} o ) — k

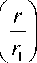
V r J J

L ₂ = c • k ^3/2 • r_m 0 • e ^{p 2} (4 • c ⁴ • k ³ • s ⁴ +

+12 • c ⁴• k² • s² - 20 • c ²• k ²• s⁴ +

+3 • c ⁴• k - 40 • c ²• k • s² + 15 • k • s⁴ -

• -    5 • c² + 15 • s ²)/(3 • p ).

L 3 =- k ^5/2 • c • r_{m 0} • e ^{- p 2} • (4 • c ⁴ • k ² • s ⁴ +

+12 • c ⁴ • k • s ² - 20 • c ² • k • s ⁴ + 3 • c ⁴ -

• -    40 • c ² • s ² + 15 • s ⁴)/(6 • p ³).

L 4 = k ^7/2 • r m o • s ² • c ³ • e- ^{p 2} • (( k • s ² + 3) • c ² - 5 • s ²)/ p ⁵,

d r m 1

^{m 01}    d S ■

L 5 =- 15 • k ^9/2 • s ⁴ • c ⁵ • r_{m 0} • e ^p 2 /(6 • p ⁷).

Особенности вычисления АК разберем подробно на примере A ₀ ⁽ _, ^D ₁⁾ в Приложении 1.

Тогда:

O ^ = ² • 5 • 4k • ^rm o X

( D ) A 0,4

= L ₁ + L ₂ + L ₃ + L 4 + L ₅.

A 2D = - 2 ■ k ^3/2 ■ s ² ■ c ■ r ₀ ² • ( e p 2 / p + i ■ П т ■ erf(i ■ p ) ) / r m ₀ .

A2D) = -2■ k3/2 ■ s■ r ■ (s2 + 2■ k■ s2 ■ c2 -

• -    2 ■ c ²) ■ i ■ П т ■ erf(i ■ p )/ r m ₀ + 2 ■ k ^3/2 ■ s ■ r_o ² ■ e p x

X ( s ² + 2 ■ s ² ■ c ² ■ k - 2 ■ c ²)/( p ■ r_{m 0} ) +

• +    2 ■ k ^5/2 ■ s ³ ■ rO - c ² ■ e p 2 /( r m о ■ p ³).

A(D = -2 ■ k3/2 ■ c ■ r02 ■ (-7 ■ s2 + 4 ■ k ■ s4 +

• +    4 ■ k ² ■ s ⁴ ■ c ² - 8 ■ k ■ s ² ■ c ² -

• -    2 ■ k ■ s ² ■ c ² + 2 ■ k ■ s⁴ + 2 ■ c ²) x

x i ■ 77 ■ erf(i ■ p) + k3/2 ■ c ■ r0 ■ ep ■ (7 ■ s2 -

• -    4 ■ k ■ s⁴ - 4 ■ k ² ■ s ⁴ ■ c ² + 8 ■ k ■ s ² ■ c ² +

• +    2 ■ k ■ s ² ■ c ² - 2 ■ k ■ s⁴ - 2 ■ c ²)/( r_{m 0} ■ p ) +

• +    k ^5/2 ■ s ² ■ c ■ r ₀ ² ■ e p ² ■ ( - 2 ■ s² - 2 ■ k ■ s ² ■ c ² +

• + 5 ■ c ² - s ²)/( r m о ■ p ³) -

• -3■ k7/2 ■ s4 ■ r0 ■ c3 ■ ep2/(rm0 ■ p5).

• ( D )

A 4,0

= -3 ■ k5/2 ■ s4 ■ c ■ r0 ■ 73 ■ i ■ 7П ■ erf(i ■ 73 ■ p) / r30 -

• - 2■ k ^3/2 ■ s ² ■ c ■ r ₀² ■ i■ 7 П ■ erf(i■ p )/(3■ r_{m 0})-

• - 3^ k⁵¹² ■ s ⁴ ■ c ■ r , ⁴ ■ e ³ p 2 /( p ■ r m 0 ) +

+ 2 ■ k3/2 ■ s2 ■ c ■ r0 ■ ep2/(3 ■ rm0 ■ p) -

• - k ^5/2 ■ s ⁴ ■ c ■ r 0 ■ e ³ p 2 /(2■ r m 0 ■ p ³).

СРАВНЕНИЕ РЕЗУЛЬТАТОВ АНАЛИТИЧЕСКОГО И ЧИСЛЕННОГО НАХОЖДЕНИЯ АБЕРРАЦИОННЫХ КОЭФФИЦИЕНТОВ

Выше были получены вклады в аберрационные коэффициенты от двух дрейфовых и дисперсионного пространства численным и аналитическим методами. Сравним полные аберрационные коэффициенты (сумму вкладов от двух дрейфовых и дисперсионного пространств) для цилиндрического зеркала. Сравниваемые данные сведены в 9 таблиц, приведенных в Приложении 2: табл.1, 4, 7 — результаты вычисления аберрационных коэффициентов ЦЗ, табл. 2, 3, 5, 6, 8, 9 — результаты вычисления проекции траекторий на ось Z.

Сравнение результатов вычисления аберрационных коэффициентов цилиндрического зеркала, полученных аналитическим и численным методами при разных значениях r0 и Py (см. Приложение 2, табл. 1, 4, 7), показывает хорошее совпадение результатов. Из этого можно сделать вывод, что и аналитический, и численный методы вычисления аберрационных коэффициентов цилиндрического зеркала работают.

В Приложении 2, табл. 2, 3, 5, 6, 8, 9, приведено сравнение результатов вычисления проекции траекторий на ось Z при тех же параметрах, что и в табл. 1, 4, 7, соответственно, в окрестности точек ( ϕ ₀ , ϑ ₀ ). Причем в табл. 2, 5, 8 проекции вычислялись при изменении ф = (0 ^ 20 ° ) и д = д ₀ = = const, а в табл. 3, 6, 9 — при ф = ф ₀ = const и изменении д = ( - 10 °^ 10 ° ). Видно, что и в том, и в другом случае величины проекций траекторий на ось Z, полученные подстановкой аналитических или численных значений аберрационных коэффициентов в формулу (5), совпадают с очень высокой точностью. Проекции траекторий на ось Z, получаемые прямым интегрированием правой части выражения (1), совпадают с хорошей точностью с результатами использования выражения (5) вдоль линии д = д ₀ = const вплоть до ф = 20 ° , а вдоль линии ф = ф ₀ = const — только до значений угла д , меньших 10 ° .

ВЫВОДЫ

Данные, приведенные в Приложении 2, табл. 1– 9, показывают, что аналитические формулы и численный метод вычисления АК дают совпадающие с высокой точностью результаты.

Вычисления по аналитическим формулам осуществляются несколько быстрее, чем численным методом.

То, что в качестве центра разложения по углу ϕ было использовано значение ϕ ₀ =0, с одной стороны, значительно упрощает процесс выведения формул и сами формулы, а, с другой стороны, относительно точки ϕ ₀ =0 такие функции, как L ^{( P )} , являются симметричными. Это приводит к тому, что все нечетные по переменной ϕ АК равны нулю.

В случае аналитических формул переход к большим порядкам АК ведет сперва к большой, а потом и к очень большой громоздкости формул. В то время как в случае численного метода вычисления АК для перехода к большим порядкам АК следует просто в программе поставить большие порядки интерполяции и увеличить точность вычисления базовых траекторий, по которым осуществляется упомянутая выше интерполяция.

Еще одним фактором, влияющим на точность конечных результатов (АК или проекция траектории на ось Z), является то, что с увеличением ф — ф ₀ и Э — 3 0 точность как аналитических формул, так и численных результатов уменьшается (как у всякой полиномиальной интерполяции при удалении от центра интерполяции). Поэтому в этом численный метод, для которого центр интерполяции может изменяться, выгодно отличается от аналитического метода.

p k 1/2

A 0 ,1 = З^ТКЯ) J"----² ■ r m 0

,                       _{0 y}

— 2

■ у ■ e ^у d у + 2 cos( 3 ₀) x

ПРИЛОЖЕНИЕ 1

Преобразование АК A _0,1 начнем с замены пе-

ременной

у ² = k sin²( 3 ₀ ) — ln

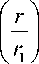
r = r1 x

x exp( k sin² ( Э ) — у ²) , d r = — 2 ■ r m о ■ у ■ e - y 2 d у .

При этом пределы интегрирования преобразуются следующим образом:

r = г ^ у = p; r = rm 1 ^ у = 0.

Подставляем все это в АК A _0,1 :

x

' p Sⁱⁿ№ ) ■ COs⁽ » 0 ) ■ ² ■ r m 0 ■ у ■ e" ' ’ ^d у

U---------- у 3----------

k 1/2 ■ r )

+------- m oi.

у ^ 0 J

.

Видно, что при у ^ 0 у одного из интегралов в подынтегральной функции содержится сингулярность. Это наблюдается у всех АК. В действительности все сингулярности взаимно сокращаются. Чтобы продемонстрировать это, все промежуточные преобразования будем проводить при условии, что r = r_{m 1} ^ у = £ . А в конечном выражении, если какие-то члены, содержащие ε , еще останутся, подставим предел £ = 0 .

A 0 D) = ^{— 2} ■ ^sin( t 0 ) ■ ^{k 1/2} ■ r m 0 ■ ^ ■ er^f( p ) +

+2 ■ c^os( t 0 ) ■ ^{( — 2} ■ ^sin( t 0 ) ■ c^os( t 0 ) ■ k 3/2 ■ r m 0 ■ i 02 ⁺

^{+ 2} ■ r m 0 ■ ^sin( t 0 ) ■ c^Os( t 0 ) ■ ^{k 3/2)/ £} ),

.     ^Pp e"^у d у     1 e"^p      .                   .

где i 0 ₂ = ----=---- i ■ V n ■ erf(i ■ p ).

₀ y ²      ε p

Видно, что члены с 1 ε (стоят в круглых скобках) в АК A _0,1 сокращаются. Аналогично происходит и во всех остальных АК.

ПРИЛОЖЕНИЕ 2

Табл. 1. Сравнение аберрационных коэффициентов для цилиндрического зеркала, полученных аналитическим (строка А) и численным (строка Ч) методами, при r 0 = 5 мм, P y =1.818182 мм, Е = 157.46272 эВ, Э ₀ = 43.5 °

Метод	A 2,0	A 2,1	A 2,2	A 4,0
А	0.0083561879	–0.0151914388	0.0166378967	0.0115541034
Ч	0.0083561879	–0.0151914388	0.0166378967	0.0115541021
Метод	A 0,1	A 0,2	A 0,3	A 0,4
А	0.0363159922	–0.0388008040	–0.3284181963	–0.0096111739
Ч	0.0363159922	–0.0388008040	–0.3284181961	–0.0096111742

Табл. 2. Сравнение проекции траектории на ось Z при r 0 = 5 мм, P y = 1.818182 мм, Е = 157.462 эВ, 5 0 = 43.5 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L z T ), подстановкой найденных аналитическим методов аберрационных коэффициентов в формулу (5) (строка L _zan) и численным (строка L z nu) методом. В верхней строке показаны последовательно ф = ф ₀ = 0 ° , ф = ф ₀ + 5 ° , ф = ф ₀ + 10 ° , ф = ф ₀ + 15 ° , ф = ф ₀ + 20 °

Метод	ф = ф 0 = 0 °	ф = ф 0 + 5 °	ф = ф о + 10 °	ф = ф о + 15 °	ф = ф о + 20 °
L z T	0.1276964045	0.1277028591	0.1277223066	0.1277550057	0.1278014140
L z an	0.1276964045	0.1277028591	0.1277223066	0.1277549908	0.1278013284
L z nu	0.1276964045	0.1277028591	0.1277223066	0.1277549908	0.1278013284

Табл. 3. Сравнение проекции траектории на ось Z при r 0 = 5 мм, P y = 1.818182 мм, Е = 157.462720 эВ, 5 0 = 43.5 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L z T ), подстановкой найденных аналитическим методов аберрационных коэффициентов в формулу (5) (строка L _zan) и подстановкой найденных численным методом аберрационных коэффициентов в формулу (5) (строка L z nu). В верхней строке показаны последовательно 5 = 5 ₀ - 10 ° , 5 = 5 0 - 5 ° , 5 = 5 ₀, 5 = 5 0 + 5 ° , 5 = 5 ₀ + 10 °

Метод	5 = 5 0 - 10 °	5 = 5 0 - 5 °	5 = 5 о	5 = 5 0 + 5 °	5 = 5 0 + 10 °
L z T	0.1256153747	0.1266647232	0.1276964045	0.1286681971	0.1295377643
L z an	0.1256153154	0.1266647215	0.1276964045	0.1286681983	0.1295377994
L z nu	0.1256153154	0.1266647215	0.1276964045	0.1286681983	0.1295377994

Табл. 4. Сравнение аберрационных коэффициентов для цилиндрического зеркала, полученных аналитическим (строка А) и численным (строка Ч) методами, при r 0 = 10 мм, P y = 7.272727 мм, Е = 127.478 эВ, 5 ₀ = 41.04 °

Метод	A 2,0	A 2,1	A 2,2	A 4,0
А	0.0063261255	–0.0097267032	0.0186543141	0.0025918275
Ч	0.0063261255	–0.0097267032	0.0186543144	0.0025918276
Метод	A 0,1	A 0,2	A 0,3	A 0,4
А	0.0191871238	–0.0224070994	–0.2176317766	0.0521608189
Ч	0.0191871238	–0.0224070994	–0.2176317764	0.0521608189

Табл. 5. Сравнение проекции траектории на ось Z при r ₀ = 10 мм, P y = 7.272727 мм, Е = 127.478 эВ, 5 ₀ = 41.04 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L _zT), подстановкой найденных аналитическим методов аберрационных коэффициентов в формулу (5) (строка L z an) и численным методом (строка L z nu). В верхней строке показаны последовательно ф = ф ₀ = 0 ° , ф = ф ₀ + 5 ° , ф = ф ₀ + 10 ° , ф = ф ₀ + 15 ° , ф = ф ₀ + 20 °

Метод	ф = ф о = 0 °	ф = ф о + 5 °	ф = ф о + 10 °	ф = ф о + 15 °	ф = ф 0 + 20 °
L z T	0.0915553589	0.0915602417	0.0915749087	0.0915994157	0.0916338568
L z an	0.0915553589	0.0915602417	0.0915749086	0.0915994153	0.0916338542
L z nu	0.0915553589	0.0915602417	0.0915749086	0.0915994153	0.0916338542

Табл. 6. Сравнение проекции траектории на ось Z при r ₀ = 15 мм, P _y = 12.727273 мм, Е = 87.32 эВ, 9 ₀ = 37.35 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L _zT), подстановкой найденных аналитическим методов аберрационных коэффициентов в формулу (5) (cтрока L _zan) и подстановкой найденных численным методом аберрационных коэффициентов в формулу (5) (строка L z nu). В верхней строке показаны последовательно 9 = 9 ₀ - 10 ° , 9 = 9 ₀ - 5 ° , 9 = 9 ₀, 9 = 9 ₀ + 5 ° , 9 = 9 ₀ + 10 °

Метод	9 = 9 0 - 10 °	9 = 9 0 - 5 °	9 = 9 о	9 = 9 0 + 5 °	9 = 9 0 + 10 °
L z T	0.0904581366	0.0910097916	0.0915553589	0.0920664097	0.0925152784
L z an	0.0904580635	0.0910097894	0.0915553589	0.0920664115	0.0925153325
L z nu	0.0904580635	0.0910097894	0.0915553589	0.0920664115	0.0925153325

Табл. 7. Сравнение аберрационных коэффициентов для цилиндрического зеркала, полученных аналитическим (строка А) и численным (строка Ч) методами, при r 0 = 15 мм, P y = 12.727273 мм, Е = 87.32 эВ, 9 ₀ = 37.35 °

Метод	A 2,0	A 2,1	A 2,2	A 4,0
А	0.0022050038	–0.0072969510	0.0295819374	0.0295819371
Ч	0.0022050038	–0.0072969510	0.0295819371	0.0024862935
Метод	A 0,1	A 0,2	A 0,3	A 0,4
А	0.0074284139	–0.0088784501	–0.1244928874	0.0852010019
Ч	.0074284139	–0.0088784501	–0.1244928870	0.0852010012

Табл. 8. Сравнение проекции траектории на ось Z при r 0 = 15 мм, P y = 12.727273 мм, Е = 87.32 эВ, 9 ₀ = 37.35 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L z T), подстановкой найденных аналитическим методом аберрационных коэффициентов в формулу (5) (строка L z an) и численным методом (строка L z nu). В верхней строке показаны последовательно ф = ф ₀ = 0 ° , ф = ф ₀ + 5 ° , ф = ф ₀ + 10 ° , ф = ф ₀ + 15 ° , ф = ф ₀ + 20 °

Метод	ф = ф о = 0 °	ф = ф о + 5 °	ф = ф о + 10 °	ф = ф о + 15 °	ф = ф 0 + 20 °
L z T	0.0537897179	0.0537914208	0.0537965472	0.0538051507	0.0538173209
L z an	0.0537897179	0.0537914208	0.0537965472	0.0538051503	0.0538173191
L z nu	0.0537897179	0.0537914208	0.0537965472	0.0538051503	0.0538173191

Табл. 9. Сравнение проекции траектории на ось Z при r 0 = 15 мм, P y = 12.727273 мм, Е = 87.32 эВ, 9 ₀ = 37.35 ° для цилиндрического зеркала, полученной расчетом этой проекции по методу работы [3] (строка L z T), подстановкой найденных аналитическим методов аберрационных коэффициентов в формулу (5) (трока L _zan) и подстановкой найденных численным методом аберрационных коэффициентов в формулу (5) (строка L z nu). В верхней строке показаны последовательно 9 = 9 ₀ - 10 ° , 9 = 9 ₀ - 5 ° , 9 = 9 ₀, 9 = 9 ₀ + 5 ° , 9 = 9 ₀ + 10 °

Метод	9 = 9 0 - 10 °	9 = 9 0 - 5 °	9 = 9 о	9 = 9 0 + 5 °	9 = 9 0 + 10 °
L z T	0.0533718658	0.0535792439	0.0537897179	0.0539865923	0.0541544042
L z an	0.0533717838	0.0535792415	0.0537897179	0.0539865945	0.0541544701
L z nu	0.0533717838	0.0535792415	0.0537897179	0.0539865945	0.0541544701