О расчете дискретных связей, работающих на сдвиг, при заданном распределении усилий между ними

По тем или иным соображениям может оказаться желательным определенное (заданное) распределение общего сдвигающего усилия между отдельными дискретными связями. Это достигается установлением соответствующей закономерности, характеризующей податливость связей.

На рис. 1 показан прямой стержень с п + 1 работающими на сдвиг связями, которые делят его на п участков. Номер того или иного участка совпадает с номером предшествующей ему связи. Нумерация начинается с конца стержня, противоположного месту приложения сдвигающей силы F

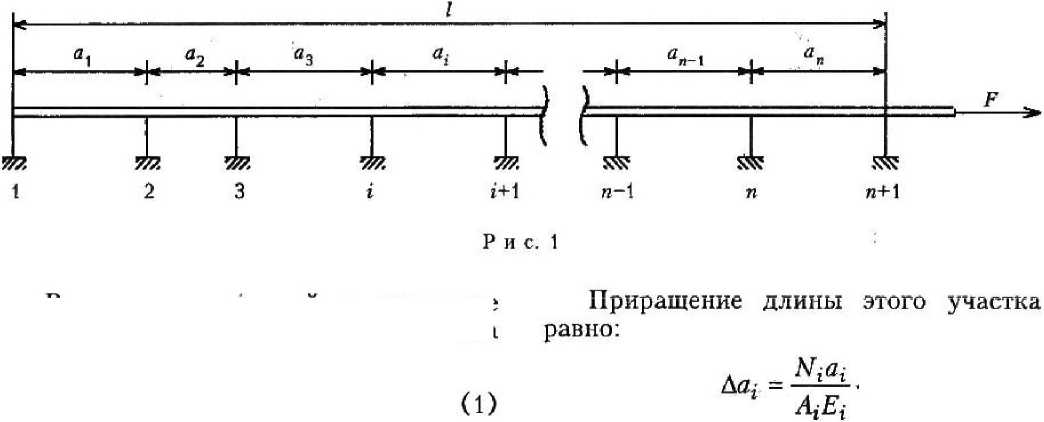
Распределение усилий, передаваемое связями, задано. Усилие, приходящееся на долю i-й связи, равно:

1 = 72+1

Поскольку ^Ti -F выполняется усло-t=i вие i=n+l

Продольная сила, действующая в пре-

Z =1

делах i-го участка, М_г = ^^, или с уче-

Л=1

том (1)

= /f КЛ.         (3)

В этом выражении а_г — длина участка; А, — площадь поперечного сечения стержня на этом участке; E_i — модуль упругости материала стержня.

Если ввести обозначение

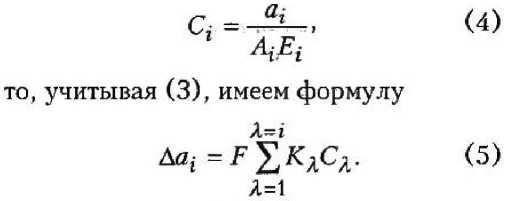
Рис. 2 дает картину работы стержня и связей па г-м участке.

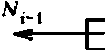
Р ис. 2

Перемещение (сдвиг) i-й связи, т. е. начала i-го участка, равно перемещению первой связи с добавлением приращений длин всех i-x участков, предшествующих этой связи. Если сдвиг i-й связи обозначить iq, а сдвиг первой связи и₁, то

Д=1-1

M,=U1+ £Л<2_м-       (6)

Д=1

Здесь в соответствии с (5)

^ц = F ^К^.    (7)

Л=1

С другой стороны, имея в виду линейный характер зависимостей, перемещение

Tz- i-и связи выразим как Uj = —, или с Gi учетом (1)

(8) Gi

Здесь G, — величина, характеризующая жесткость связи (усилие, требующееся для единичного сдвига).

Сопоставляя (6) и (8), получаем:

у v ц=г-\

F^- = F^ ^ «>

Здесь G1 — жесткость первой связи.

Преобразование формулы (9) с учетом (7) приводит к выражению

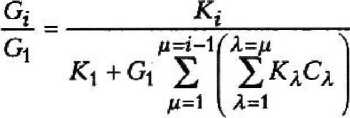
Наибольшее перемещение получает (п+1)-я связь, находящаяся в месте приложения сдвигающей силы.

Если его величина задана и равна Д д=п то согласно формуле (6) щ = f - IL^-

К

Поскольку u\ = F —-. из этого равенства Gi вытекает, что должно выполняться условие, выражаемое формулой

¹ д=п f- 'L^y

Д-1

Таким образом, при детерминированном максимальном сдвиге крайней (самой близкой к месту приложения силы) связи во все предыдущие формулы в качестве G1 должна подставляться величина, определяемая по формуле (И).

Если связь «1» неподвижна (рис. 3), т. е. Gj = оо, из формулы (9) получаем:

61=^ ^^   <12)

V д=1

Рис. 3

симметричного относительно своей середины стержня, на концы которого действуют в противоположных направлениях одинаковые силы (рис. 4). Здесь в роли неподвижной опоры выступает названная середина стержня.

Аналогично обстоит дело в случае

Рис. 4

Если все участки стержня одинаковы, имеют каждый длину а = — (где I — пол-h ная длина стержня), площадь поперечного сечения А, модуль упругости Е и одну а и ту же величину с =---, вышеприве-

АЕ денные формулы упрощаются. В этом случае подставляемые в (10) суммы выражаются следующим образом:

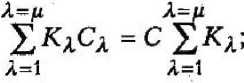
^-ХГХ-ц

= с£ £хл Д=1 ^=1

}1-г-\(Х=ц.       '

£ £^сл

д=1 (л=1      )

Если к тому же задается равномерное распределение сдвигающего усилия меж-

F ду всеми связями, т. е. Т -----. имеем.

п + 1

к,=к2 =...........= к„+1 =

= к = ^-        <13> п + 1

Входящие в формулу (10) суммы приобретают значения

^К^С = цС, Л=1

ц-i-lf Х=и

д-1 I, Л-1

= ^i(i-1).

Имея в виду (4) и приняв обозначение

В = 2^,          (14)

АЕ формулу (10) для случая равномерного нагружения связей представляем в виде

_        1

^G1 1 ₊ 191 ~ у 2

Если полная длина стержня равна I = па, то, как нетрудно найти, ее прира-

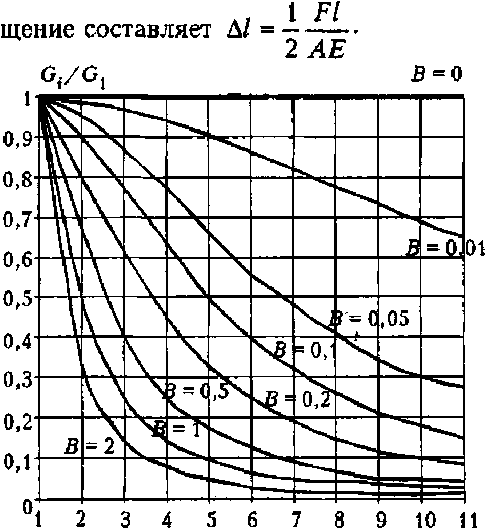
Р ис. 5

Графики, приведенные на рис. 5, показывают, каков должен быть характер изменения жесткости равномерно нагруженных связей при неко-

Поступила 14.12.02.

торых значениях параметра В (расчет сделан по формуле (15) для равпопро-летного стержня с одиннадцатью связями).

К РАСЧЕТУ МНОГОЭТАЖНЫХ ЗДАНИЙ

НА ИМПУЛЬСНЫЕ НАГРУЗКИ

К импульсным нагрузкам можно отнести воздействия ударных волн при взрывах и сейсмические силы. При проектировании зданий учитывают определенную вероятность их появления и величину. О силе этих нагрузок можно судить по последствиям землетрясений в Ташкенте и Спитаке, по взрывам домов в Москве и других городах.

Представляет интерес проанализировать случаи, когда взрывы происходили на разных этажах зданий. Если они про- i/r'vnnirnTi urn ттоппл^л пгтпи/о тл гггкг¹-то rn^TT) т ?гт АИ-АМ^АА^ДА! 11С4 4A*-p*->V4^vl ^ACVIXV, IV 11 W^A^/^V А ОГ1Л были более катастрофическими, чем при взрывах на более высоких этажах. Это говорит, хотя и косвенно, о влиянии степени нагруженности сжатых конструкций на их сопротивляемость поперечным силам от ударных воздействий. Поэтому возникает необходимость анализа известных методов расчета внецентренно сжатых железобетонных элементов при действии поперечных сил.

В действующем СНиПе [4] даются расчеты на поперечную силу изгибаемых элементов, обжатых до определенной степени продольными силами. В действительности они очень существенны и могут достигать предельных значений. В этих условиях восприятие еще и поперечных сил сомнительно. Для проверки возможности использования методики СНиПа [4] при расчете сил внецепт-ренно сжатых железобетонных элементов на поперечную силу использована методика 12; 3J, имеющая другую интерпретацию взаимовлияния продольных и поперечных сил в элементе.

Сравнение методик проведем на конкретных примерах аналитически и качественно по таким их свойствам, как универсальность, модность и красота [1].

В СНиПе [4] учет продольных сил в железобетонных элементах, рассчитываемых по поперечной силе, производится по формулам

Q^Qb^tW- <0 Qb= Фьз^ ⁺ ^ ^Rbtbho/c; (2)

n = ^,\P/R_btbh^

Яsw~ Asw^sw/s ’        ^^

где Q — несущая способность элемента по поперечной силе; Q_b — поперечная сила, воспринимаемая бетоном; q^^. — усилие в поперечной арматуре па 1 см погонной длины; с — проекция наклонного сечения на продольную ось элемента; у^^ — коэффициент; b, hn — ширина и рабочая высота сечения элемента; Р - сжимающее усилие в элементе; R_bt — расчетное сопротивление бетона на растяжение; А_$№ — площадь сечения поперечной арматуры; R_$m — расчетное сопротивление поперечной арматуры на растяжение; 5 — шаг поперечной арматуры.