О расчете параметров двухмассовой термодинамической модели асинхронного двигателя

Асинхронные двигатели (АД) – самый распространенный тип электродвигателей в промышленности. Они составляют около 90 % всего парка машин [1]. Ежегодный выход этих двигателей из строя составляет от 10–12 до 20–25 % [2-5]. Значительная доля выходов АД из строя связана с повреждением обмоток статора [6], в том числе по причине перегрева, вызванного неадекватными условиями эксплуатации [7]. Эти обстоятельства обусловливают важность правильной оценки теплового состояния АД как в ходе эксплуатации, так и при проектировании электропривода.

Используемые во многих случаях методы оценки теплового состояния АД базируются на слишком существенных упрощениях. Так, классические методы средних потерь и эквивалентных величин основаны на одномассовой модели нагрева. В то же время, для оценки теплового состояния двигателя в задачах электропривода (в отличие от задач электромашиностроения) требуются не статические, а динамические модели нагрева, а одномассовая модель совершенно неадекватно отражает динамику температуры обмоток двигателя. Также классические методы не учитывают нелинейность связи скорости термического старения изоляции с температурой обмотки, что также актуально для задач электропривода, когда рассматриваются режимы работы с изменением температуры обмоток в широком диапазоне. В таких случаях требуется использовать подходы на основе экви-валентирования режимов работы по скорости старения изоляции, что требует использования математического моделирования [8].

Существует два подхода к моделированию тепловых процессов в электрических машинах численными методами – моделирование на основе тепловых схем с сосредоточенными параметрами и на основе методов, связанных с пространственно-временной дискретизацией объекта исследования. Последние для решения задач термодинамического моделирования обычно требуют построения трехмерных моделей [9, 10], что предопределяет очень высокие требования к вычислительным мощностям и длительное время решения подобных задач. Термодинамические модели (ТДМ) на основе тепловых схем предъявляют значительно меньшие требования к вычислительным ресурсам и обеспечивают сравнительно быстрый расчет, что позволяет использовать их при решении задач, связанных с перебором значительного количества вариантов [10-12]. По этим причинам создание моделей на основе тепловых схем является актуальным.

При построении многомассовой ТДМ для расчета ее параметров требуется большой объем информации о двигателе. Такая информация, как правило, доступна только при проектировании электрических машин. Специалисты, работающие в области электропривода, в большинстве случаев не имеют доступа к полной информации, необходимой для расчета параметров сколько-нибудь сложной ТДМ. Это позволяет сделать вывод о том, что особое значение в практическом плане приобретает двухмассовая ТДМ АД. Такая модель требует небольшого объема информации для определения своих параметров, но, в отличие от одномассовой модели, позволяет значительно точнее воспроизводить динамику температуры наиболее критичных к нагреву частей АД за счет выделения этих частей в отдельный узел [13, 14]. Этот вывод определяет необходимость разработки способов определения параметров двухмассовой ТДМ АД при ограниченном объеме информации о двигателе. Дополнительный интерес к определению параметров двухмассовых моделей АД вызывает и возможность использования их для построения средств защиты электродвигателя [15, 16].

Таким образом, встает задача получения простых аналитических соотношений, пригодных для расчета параметров двухмассовой ТДМ АД при ограниченном объеме исходных данных. Здесь наибольшую сложность представляет определение тепловых проводимостей этой модели.

Математическое описаниедвухмассовой ТДМ

Рассмотрим двухмассовую модель АД, в которой первый узел представляет собой обмотку статора, а второй – остальную часть машины. Теп- ловые процессы в такой модели описываются двумя дифференциальными уравнениями, получаемыми из уравнений термодинамического баланса:

С 1^ + Л 11 Т 1 -Л 12 Т 2 = д Р 1 ;

С ^dT2

² dt

—

^ 21^Т1 + ^ 22^Т2 ^{— Д} Р 2 ,

где C1 и C2 – теплоемкости элементов, отнесенных к первому и второму узлу модели; АР 1 и АР2 - мощности потерь в этих узлах; т1 и т2 - превышения температуры соответствующих узлов над температурой охлаждающей среды; Х12 - тепловая проводимость между первым и вторым узлом (здесь полагаем, что Х21= Х12); Хп = Х10 + Х12; Х22 = Х20 + Х12; Х10 и Х20 - тепловые проводимости от узлов модели к охлаждающей среде.

Если пренебречь влиянием температуры на теплоемкости и теплопроводности модели, то система (1) может рассматриваться как линейная. В этом случае для неизменных во времени мощностей потерь ее аналитическое решение выглядит следующим образом:

Т1 = А 16xp(- 1/Т1) + А2exp(- I^Ht^ ; (2)

Т 2 = А ₃exp ⁽ - 1/Т 1 ) + А ₄exp ⁽ - 1 ^/ Р 2⁾ +т 2уст , (3) где A 1 , A 2 , A 3 , A 4 – постоянные, зависящие от начальных условий и мощности потерь; т _1уст - установившееся значение превышения температуры первого узла модели (обмотки статора) над температурой охлаждающей среды

^Т 1уст ^{— (} ^ 12^Д ^ 2 ⁺ ^ 22 ^^ 1⁾⁽ ^ 11 ^ 22 ^— ^- 12 ) ^{1 ; (4)}

т _2уст - установившееся значение превышения температуры второго узла модели над температурой охлаждающей среды

Т 2уст = (Л 12 ДР 1 + Л 11 ДР 2 )(Л 11 Л 22 — Л 12 ) " ¹ ; (5)

Т ₁ и Т ₂ – постоянные времени ( Т ₂> Т ₁).

Значения постоянных времени Т1 и Т2 опреде- ляются модулем обратной величины корней характеристического полинома системы (1):

T ! = 2 С 1 С 2 [ С 1 ^ 22 + С 2 ^ 11 + О] - ¹ ;        (6)

T 2 = 2 С 1 С 2 [ С 1 Л 22 + С 2 Л 11 — О] ^-1 ,        (7)

где

О — (С 2 ^ 11

—

: )0^.

2С 1 С 2 Х 11 Х 22 + с 2 ^ 22 + 4С 1 С 2 ^ 22

Соотношения для определения параметров двухмассовой ТДМ

Решением системы (1) для номинального ус- тановившегося режима являются величины т1устN и т2устN. В качестве т1устN примем допустимую величину превышения температуры обмотки по ГОСТ. Тогда т2устN можем выразить как т2устN =9Nт1устN, что дает возможность записать решение системы (1)

для номинального установившегося режима в виде

^ 11 ^— ^ 12 ^ N — Д^ 1М^/т1устМ^;

^ 22 ^ W ^— ^ 12 ^{— Д} ^ 2М / ^Т1устМ .

В систему (8) входят три неизвестные вели- чины тепловых проводимостей, кроме того, она не содержит информации о величинах теплоемкостей С1 и С2, определяющих динамические свойства модели. Величина ϑN также в общем случае неизвестна. Следовательно, для определения всего необходимого набора параметров двухмассовой ТДМ требуется дополнительная информация.

Учтем, что для ТДМ в электроприводе очень важно обеспечить адекватное воспроизведение моделью динамики изменения температуры при переходных процессах. Поэтому для дополнения информации, содержащейся в уравнениях (8), вос- пользуемся выражениями для постоянных времени (6) и (7).

Следуя [17, 18] можно применить теорему Виета к характеристическому уравнению системы (1), связав коэффициенты этого уравнения с по- стоянными времени системы, что дает возможность представить систему уравнений (6), (7) и (8) в более компактной форме:

^ 11 ^— ^ 12 ^ N ^{— Д} Р 1Н / ^Т1устН^;

^ 22 ^ N ^— ^ 12 ^{— Д} Р 2Н / ^Т1устН^;

Л 11 С 1 ^-1 + Л 22 С 2 ^-1 — ТГ¹ + г , ^-1 ;

^ 11 ⁺ ^ 22 ^— ^ ² 2 ^— С 1 С 2 Т 1 ^{1 Т}2 ¹ .

Система (9) позволяет определить четыре неизвестных параметра. Однако этого недостаточно даже при известных величинах теплоемкостей. Поэтому требуется дополнительное уравнение.

В литературе, в частности в [19], показано, что наибольшая постоянная времени при модели- ровании нагрева двигателя с использованием многомассовой термодинамической схемы остается практически одинаковой для процессов во всех элементах этой модели. Физически это объясняет- ся процессами перераспределения тепла между элементами двигателя [20], продолжительность которого при неизменной величине потерь определяется в конечном счете элементами с наибольшей тепловой инерцией.

Постоянная времени системы n тел, от которой зависит общая длительность тепловых переходных процессов в этой системе, определяется следующим образом [21]:

Т —Е ?-1 с i R i , (10) где C_i – теплоемкость i -го тела; R_i – тепловое сопротивление от i -го тела до охлаждающей среды.

Ri — Л-1 + ЕЙ (-^ + ^^^, (11) i 0 ^fc-1 \^крк 2l.F.), где 5i и 5k - характерный размер тела в направлении теплового потока; li и lk – удельная теплопроводность материала соответствующего тела; Fi и Fk – площадь поверхности соответствующего тела; Хо - теплоотдача непосредственно в охлаждающую среду. В выражениях (10) и (11) использована нумерация, начинающаяся от охлаждаемой поверхности.

Применительно к термодинамическим моделям, где все элементы рассматриваются как точечные, выражение для теплового сопротивления R_i (11) можно записать с использованием тепловых проводимостей между телами:

R i = A - ¹ + Z fc-- ¹ i X - _k ¹ , (12) где слагаемое E fc^ X - ¹ представляет сумму тепловых проводимостей от i -го тела к охлаждающей среде по всем путям.

Подставив (12) в (10), получим:

т — х - ¹ !^ с , +E L-K с i Z fc-U-D . (13)

Сумма E k-i A ^-1 в выражении (13) существует только для i >1. С учетом того, что нумерация индексов в выражении (13) идет от охлаждающей среды к i -му элементу, можно констатировать, что применительно к двухмассовой ТДМ во втором слагаемом этого выражения будут присутствовать только те составляющие, которые содержат теплоемкость, соответствующую обмотке двигателя, то есть C ₁ при использовании системы индексации величин, принятой нами в настоящей работе. В двухмассовой ТДМ с выделением обмотки статора в отдельный узел C 1 << C 2 . Тепловые проводимости между медью обмотки и сталью статора, как показывают расчеты, превышают величину теплоотдачи от двигателя во внешнюю охлаждающую среду. Приведенные факты означают, что для такой двухмассовой ТДМ будет выполняться условие A - ¹ ^ '- _] С , >> ^р . ( С i Е^Х -, ¹ ) и постоянная времени Т , определяющая общую длительность теплового переходного процесса, должна быть близка по величине к первому слагаемому выражения (13), которое совпадает с выражением для постоянной времени нагрева одномассовой ТДМ.

Изложенное выше дает возможность в допол-

нение к системе (9) получить еще одно уравнение для определения параметров тепловой схемы замещения. Просуммировав уравнения системы (1) и

полагая т 1 = т ₂= т , получим следующее уравнение тепловых процессов в одномассовой ТДМ, записанное через параметры двухмассовой модели:

(С1 + С2) — + (Хц + Х22 - 2Л12)Т =

at

= ДР1 + ДР 2.

Решение уравнения (14) содержит одну экспоненту с постоянной времени T , определяемую обратной величиной корня характеристического уравнения:

Т = ( С 1 + С 2 )(Л 11 + Л 22 - 2A 12 ) ^-1 . (15)

Введем коэффициент к _т — Т₂/Т. С учетом этого коэффициента, значение которого для двигателей закрытого исполнения можно принять равным единице, получим из (15) дополнительное уравнение, используемое для нахождения параметров двухмассовой ТДМ. Путем несложных преобразований из системы, содержащей уравнения (9) и (15), можно исключить постоянные времени T 1 и T 2 , перейдя к системе из трех уравнений:

Х 11    X 12 &_N — ^Д Р 1М^{/ т} 1 уст М^;

^ 22 ^ W    ^ 12 ^{— Д Р} 2N^{/ т} 1 уeт N ;

^Ц^ 22^- ^ 12

^Т Х₁₁+Х₂ 2^-2 ^ 12

С 1 С 2

С 1 + С 2

Г^И + ^22.

L С 1     С 2

-

Х 11 +Д 22 “2А 12

k r ( С 1 + С 2 )

]•

Выполним оценку величины ϑ N на основе многомассовой ТДМ АД. Для этого используем выражение, устанавливающее соотношение между средневзвешенными значениями превышений температуры узлов многомассовой модели, входящих в состав первого (Т_1устМ) и второго (Т_2устМ) узлов двухмассовой ТДМ при работе в установившемся номинальном режиме:

^ ^Т2устМ ^/т1устМ . ⁽¹⁷⁾

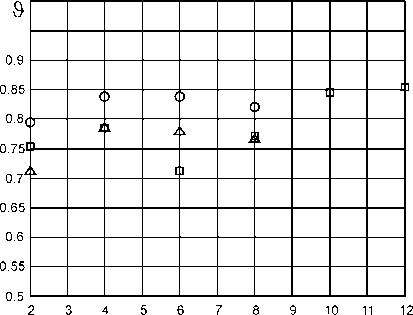
На рис. 1 и 2 представлены величины ϑ, рассчитанные по (17) с использованием пятимассовой ТДМ для некоторых двигателей серии 4А закрытого исполнения (обозначено: 2 p – число полюсов). Из этих рисунков следует, что явно выраженной зависимости ϑ от габаритов и числа полюсов АД закрытого исполнения нет. Значения ϑ в среднем близки к 0,8. Аналогичные значения ϑ получаются и для двигателей закрытого исполнения других серий, например для двигателя MTKF012-6 величина ϑ составляет 0,84. При определении параметров двухмассовой ТДМ можно полагать, что ϑ N = ϑ и ориентироваться для АД закрытого исполнения на приведенные выше значения.

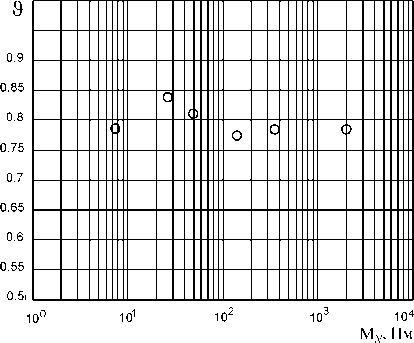
Рис. 1. Зависимости ϑ от номинального момента для двигателей 4A80A4, 4A100L4, 4A132S4, 4A180S4, 4A225M4, 4A355M4

2?

Рис. 2. Зависимости ϑ от числа полюсов для двигателей серии 4А с высотой оси 100 мм ( о ), 225 мм ( А ) и 355 мм ( □ )

Учет особенностей двигателя закрытого исполнения

Особенностью процессов нагрева закрытых АД является то, что тепловой поток от обмотки статора к охлаждающей среде идет через внутренний корпус, то есть проходит через второй узел двухмассовой ТДМ. Именно этот факт и делает большую постоянную времени T ₂ этой модели близкой по величине к постоянной T одномассовой модели. Использование равенства T ₂ = T , заложенного в систему уравнений (16), приводит и к наличию определенных соотношений между теплоемкостями и тепловыми проводимостями двухмассовой термодинамической модели, то есть величинами, от которых соответствующие постоянные времени зависят. Запишем третье уравнение системы (16) через Х ₁₀ и Х ₂₀ при k _T = 1:

^Ю^ 2о + ( ^ю + ^ 2о ) ^ 12 _ С 1 С 2 х ^ 10⁺ ^ 20            ⁽ С 1 + С 2 ⁾²

х      + Х12) с2 + (х20 + х12) с1 + 2X12j.

Введем обозначения: l = Х ₁₀/ Х ₂₀ и с = С 1 / С ₂, с учетом которых выражение (18) запишется как

I+7 X 20 + ^Х12 ^_

.■'■■■"•• I .<19)

Из (19) путем несложных преобразований получаем равенство l = c , то есть:

Х10С2 _ Х20С1.(20)

Выразив тепловую проводимость Х ₁₀ из (20) через Х ₂₀ и теплоемкости, получаем возможность свести количество неизвестных в системе (16) до двух (при известных значениях С ₁ и С ₂). Это дает возможность использовать для нахождения тепловых проводимостей только первые два уравнения в системе (16), записав их следующим образом:

^Х20 ^С 1 ^С 2 ^{1 + (1}    ^ ^^)Х12 ^_ ‘^ 1М^/т1устМ ;

^X20 ^ ^ - ⁽¹ - ^ ^^)Х12 ^_ △ ^ 2^^/т1уст^ .

Решая систему (21) относительно Х ₂₀ и Х ₁₂, получим выражения для всех тепловых проводимостей двухмассовой модели:

^Х20 _ т-Ь-. -^ ;

.-^5£17+^ ;

Х _   ^dN С 2 ‘P 1N -С 1 ‘P 2N

^{12    T}1ycmN^(1— ^ N^{)( С} 1⁺ ^ N ^С 2 ) .

Воспользовавшись выражениями (6) и (7) для постоянных времени, при выполнении условия (20) получим:

Т 1 _(Х 22 / С 2 +Х 12 / С 1 ) ^-1 ;              (25)

T ₂ _ С 2 /Х 20 .

Поскольку Х ₂₂/ C ₂<< Х ₁₂/ C 1 , из (25) вытекает приближенное соотношение: T 1 - C 1 / Х ₁₂. Этот результат хорошо соответствует выражению (13) с учетом того факта, что теплоотдача в окружающую среду от обмотки статора в двигателях закрытого исполнения мала по сравнению с тепловой проводимостью к элементам, составляющим вторую массу двухмассовой ТДМ, что предопределяет соотношение Х ₁₀<< Х ₁₂.

Проанализируем взаимосвязи отношения превышений температур в номинальном режиме работы ( 3 N ) с параметрами двухмассовой ТДМ. Запишем выражения (4) и (5) для номинального режима в виде:

т1уст^

‘£ 1N ^ 2g +(‘£ 1N +‘£ 2N )^ 20 .

^ 10 ^ 20 ^{+ (} ^ 10⁺ ^ 20 )^ 12   ’

_ ‘^ 2N⁺ ^ 1ycmN ^ 12

^{Т 2уст} " ^_    Л₂ 0 ₊ Л₁₂

^V

0.95 -

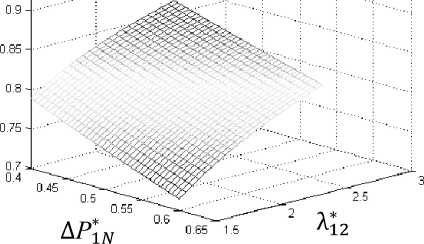
Рис. 3. Зависимость $ N от ДР^ и ^ 12 для АД закрытого исполнения

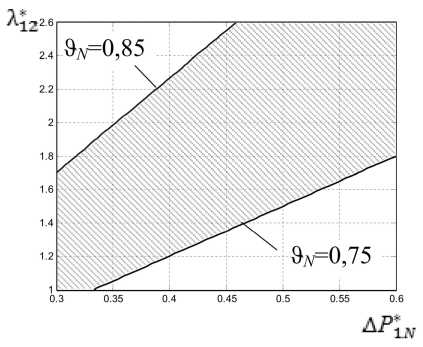
Рис. 4. Линии уровня поверхности $ N = f ( Д Р 1n , Г 12 ) для АД закрытого исполнения

Из (27) и (28) получим:

В

N

_ ^T2ycmN     ^ 12     ।

^T1ycmN     ^ 20 +^ 12

+

^ДP2N       ^ 10 ^ 20 ⁺ С^ 10⁺ ^ 20 )^ 12

■

-----------------------------------:--------------------------------------------------.

^ 20⁺ ^ 12 ^1N ^ 20 ^{+ (} A ^P1N⁺^2N )^ 20

На рис. 5 приведены кривые нагрева двигателя 4A100L4. Здесь 1 и 2 – температуры лобовых (1) и пазовых (2) частей обмотки статора, рассчитанные с использованием пятимассовой ТДМ, 3 – превышение температуры для первого

Для анализа зависимости ϑ _N от параметров двухмассовой ТДМ введем относительные единицы. В качестве базисных величин примем: Д б = < Х 0 = ^ 10 + ^ 20 ; Д Р б = Д Р ^ = Д Р 1 N + Д Р 2 N. В этом случае выражение (29) может быть преобразовано

к виду:

B_N_  ^  +

^N    1-А 10 +А 12

। ^1-ДР1N , ^ 10^(1- ^ 10⁾⁺ ^ 12

^1- ^ 10⁺ ^ 12 ^ДP1N ( ^1- ^ 1o ) ⁺ ^ 12

Из (30) видно, что при Л ^ _о< ДР₁ * _N всегда ϑ _N < 1. Поскольку для двигателей закрытого исполнения А ^ _о весьма мала, а мощность потерь в обмотке статора составляет существенную долю суммарной мощности потерь в номинальном режиме, для закрытых АД всегда выполняется соотношение ϑ _N < 1.

На рис. 3 показана зависимость 3 N от ДР₁ * _N и Х [ ₂ для АД закрытого исполнения, построенная по соотношению (30) при А ^ _о=0, а на рис. 4 показаны линии уровня поверхности 3 _N = f( ДР^, Х *₂ ), изображенной на рис. 3. Штриховкой отмечена область значений ДР^ и Л ^ ₂, при которых 0,75< 3 N <0,85.

Из рис. 3 и 4 следует, что для закрытых АД при широком диапазоне изменения величин ДР ^ _N и Л ^ ₂ значение 3 N меняется мало, оставаясь в пределах 0,8 + 0,05. Это подтверждает вывод о величине ϑ _N , сделанный выше с использованием пятимассовой ТДМ, и дает основания использовать указанный диапазон 3 N при определении тепловых проводимостей двухмассовой ТДМ АД закрытого исполнения.

узла двухмассовой модели с тепловыми проводимостями, рассчитанными по (22), (23) и (24)

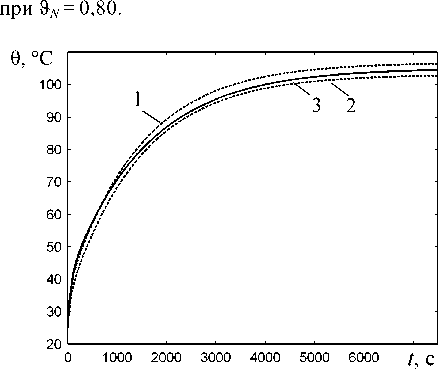
Рис. 5. Кривые нагрева двигателя 4A100L4

Заключение

• 1.    Обоснована целесообразность использования в задачах электропривода для оценки теплового состояния АД двухмассовой термодинамической модели с выделением в качестве отдельного узла обмотки статора.

• 2.    Получено математическое описание двухмассовой термодинамической модели и выполнен его анализ.

• 3.    Получены аналитические соотношения, пригодные для определения тепловых проводимостей двухмассовой термодинамической модели асинхронного двигателя закрытого исполнения при минимальном наборе исходных данных.