О расчете спектров вибрации и шума при обработке шарико-стержневым упрочнителем коробчатых деталей

Введение. Виброударная отделочная обработка шарико-стержневым упрочнителем (ШСУ) относится к категории упрочняющих технологий, у которых технологическая нагрузка представляет собой последовательность ударных импульсов на соответствующую поверхность обрабатываемого изделия. Эти процессы при всех их преимуществах с точки зрения обеспечения качества изделий, производительности, обладают существенным недостатком, поскольку неизбежно сопровождаются высоким уровнем излучаемого шума как самой заготовкой, так и корпусом упрочнителя. Исследования в области моделирования шумообразования проведены только для деталей типа тел вращения, для условий шарнирного и консольного закрепления [1] на базе универсальных токарно-винторезных станков, т.е. при вращающейся заготовке.

Между тем чрезвычайно широкий спектр плоских деталей, деталей прямоугольного сечения и корпусных подвергается обработке ШСУ на фрезерных станках, способы закрепления, акустическая система которых существенно отличаются от универсальных токарно-винторезных. Поэтому существующие модели процесса шумообразования для цилиндрических поверхностей неприменимы для расчетов акустических характеристик вышеописанных деталей.

Детали представляют собой полые тонкостенные прямоугольные параллелепипеды и характеризуются максимальным отношением площадей, излучающих звук поверхностей и изгибной жесткости. Поскольку они представляют собой систему энергетически замкнутую с малым значением коэффициента потерь колебательной энергии, то расчет их вибраций основан на уравнениях энергетического баланса [2], традиционно используемого для моделирования подобных конструкций.

Вывод зависимости для расчета виброскоростей коробчатых деталей. Специфика расчета заключается в том, что вводимая в заготовку колебательная мощность (энергия) определяется процессом обработки ШСУ. Обозначим: 1 – передняя стенка; 2 – левая стенка; 3 – задняя стенка; 4 – правая стенка; 5 – дно. Система уравнений энергетического баланса для такой детали имеет вид:

8 1 S 1 q i + ^а 12 / 12 q i + ^a i5 / 15 q i + ^a i4 / 14 q i — ^a 2i l 21 q 2 + 0. 4, ¹ ₁4 q 4 + О. _д| ^5 q 5 ,

⁸ 2 ^S 2 q 2 + ^a 21 ¹ 12 q 2 + ^a 23 ¹ 23 q 2 + ^tt 25 ¹ 25 q 2    ^a i2 ¹ 12 q 1 + ^tt 32 ¹ 23 q 3 + ^tt 52 ¹ 25 q 5 ,

⁸ 3 ^S 3 q 3 + ^a 32 ¹ 23 q 3 + ^a 34 ¹ 34 q 3 + ^tt 35 ¹ 35 q 3 ^{— tt} 23 ¹ 23 q 2 + ^tt 43 ¹ 34 q 4 + ^tt 53 ¹ 35 q 5 + ^N ,

⁸ 4 ^S 4 q 4 + ^a 41 ¹ 14 q 4 + ^a 43 ¹ 34 q 4 + ^tt 45 ¹ 45 q 4    ^M ¹ 14 q 1 + ^tt 34 ¹ 34 q 3 + ^tt 54 ¹ 45 q 5 ,

85S5q5 + a51151 q5 + a52125q5 + tt53135q5 + tt54145q5   tt15115q1 + tt25125q2 + tt35135q3 + tt45145q5 , где δi – коэффициент поглощения, 1/м; qi – энергетические потоки в стенках, Вт/м; Si – площадь стенки, м2; αij – коэффициент передачи энергии между стенками; N – мощность, вводимая в корпус при обработке ШСУ, Вт; lij – длина линии контакта между двумя соседними стенками, м.

Систему уравнений (1) для чугунной корпусной для удобства проведения расчетов на ЭВМ:

представим в матричной форме

детали

-

-

-

K 1	-α 21 l 12	0	-α 41 l 14	-α 51 l 15		q 1		0
α 12 l 12	K 2	-α 32 l 23	0	-α 52 l 25		q 2		0
0	-α 23 l 23	K 3	-α 43 l 34	-α 53 l 35	×	q 3	=	N
α 14 l 14	0	-α 34 l 34	K 4	-α 54 l 45		q 4		0
α 15 l 15	-α 25 l 25	-α 35 l 35	-α 45 l 45	K 5		q 5		0

, f1i

K ₁ = 0, 03 η      + α ₁₂ l ₁₂ + α ₁₄ l ₁₄ + α ₁₅ l ₁₅ ;

\ h ₁        12 12      14 14      15 15

где

K ₂ = 0, 03 η      + α ₂₁ l ₁₂ + α ₁₄ l ₁₄ + α ₁₅ l ₁₅ ;

h ₂

f

K ₃ = 0, 03 η    ^{3 i} + α ₃₂ l ₁₂ + α ₁₄ l ₁₄ + α ₁₅ l ₁₅ ;

K 4 = 0,

K 5 = 0,

03 η _h ^{f 4} ₄ ⁱ

03 η _h ^{f 5} ₅ ⁱ

+ α 12 l 12 + α 14 l 14 + α 15 l 15 ;

+ α 12 l 12 + α 14 l 14 + α 15 l 15 ;

η i – коэффициенты потерь энергии в стенках корпуса; h i – толщина соответствующей стенки, м;

f i – собственные частоты колебаний стенок, Гц.

Решение системы (2) может быть выполнено по методу Крамера и для энергетического потока в первой стенке имеет вид:

		0	-α 21 l 12	0	-α 41 l 14	-α 51 l 15
		0	K 2	-α 32 l 23	0	-α 52 l 25
		N	-α 23 l 23	K 3	-α 43 l 34	-α 53 l 35
		0	0	-α 34 l 34	K 4	-α 54 l 45
		0	-α 25 l 25	-α 35 l 35	-α 45 l 45	K 5
q 1 =		K 1	-α 21 l 12	0	-α 41 l 14	-α 51	l 15	.                             (3)
	-α 12 l 12		K 2	-α 32 l 23	0	-α 52 l 25
		0	-α 23 l 23	K 3	-α 43 l 34	-α 53 l 35
	-α 14 l 14		0	-α 34 l 34	K 4	-α 54 l 45
	-α 15 l 15		-α 25 l 25	-α 35 l 35	-α 45 l 45	K 5

Необходимо отметить, что система уравнений (1) записана для случая, когда обрабатывается стенка 3. Когда упрочнитель будет воздействовать на другую стенку, то в соответствующем уравнении в правой части будет добавляться мощность, вводимая в корпус при обработке ШСУ, и система будет решаться аналогичным образом.

Коэффициент прохождения энергии изгибной волны из стенки в стенку (α ij ) [2] и собственные частоты колебаний определяются по известным формулам:

^a j = ²

2,5

А)

1 +

2,5

:   )

-2

V

n

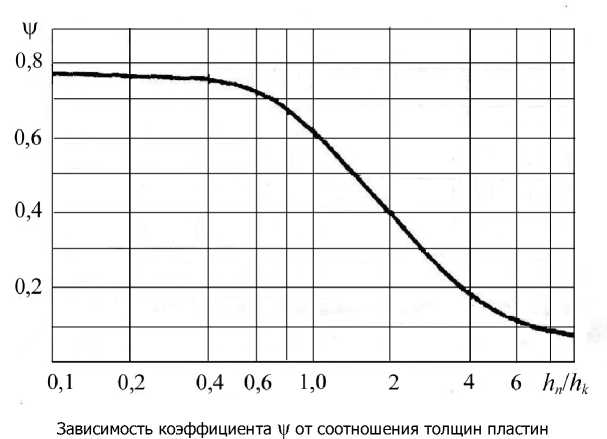
где h i , h j – толщины стенок, м; ψ – функция, учитывающая соотношение толщин пластин (определяется по графику, см. рисунок).

Собственные частоты колебаний пластины определяем по формуле [2]:

f n =П h

E

3 p (1 -ц ² )

( 2     2 A m n I

1 ^{2 +} 12 J

V 1       2 )

где μ – коэффициент Пуассона; h – толщина пластины, м; l 1 и l 2 – длина и ширина пластины, м; ρ – плотность, кг/м³; Е – модуль упругости, Па; m и n – постоянные числа, определяющие форму колебаний.

На основании рассчитанных энергетических потоков определяем скорости колебаний стенок и с учетом зависимостей [2] получаем следующее выражение:

v,= 0,07 q i^⁵ m 00^ ( f , h , )^{- 0}’²⁵ ,                                            (4)

где m ₀ – распределенная масса стенки, кг/м².

Значение

/                \ 0,125

_v 3 P( T -; 2) _v

для стали в 1,06 раза больше, чем для чугуна. Поэтому для тех-

нических расчетов шума не только чугунных, но и стальных корпусов эта величина может быть принята постоянной и равной 0,135 (м/с)0,25.

Учитывая зависимость виброскорости (4), получаем формулу для расчета звуковой мощ- ности такого источника в следующем виде:

W ист =6 - 10 ^{- 6}

q S ^{h 2}

/   2      2 A 0,5

m n I

По полученным зависимостям находим уровни виброскорости и звуковой мощности соответственно:

Lv = 10lg qm о - 5lg ( fh ) + 123 ,       Lw = 10lg q , + 10lg S , - 20lg h , - 5lg m - + n- 1 + 68 .    (5)

ll

V h      2!

Как видно из выражения (5), снизить уровни шума реально можно только за счет уменьшения значений эффективного коэффициента потерь колебательной энергии. Технически это можно реализовать различными способами. Более технологичными и эффективными являются использование сыпучих поглотителей и вибродемпфирование стенок корпусной детали. В этом смысле практический интерес представляет обратная задача – теоретическое определение требуемых частотно-зависимых значений коэффициентов потерь колебательной энергии, вычисленных по критерию выполнения санитарных норм шума. Для этого в левую часть выражения (5) подставим предельно допустимые значения, уменьшенные на 4-5 дБ. Такая поправка должна быть учтена при условии одновременной работы нескольких установок ШСУ. Поскольку аналитически коэффициенты потерь колебательной энергии из системы уравнений (2) не выражаются, то из зависимости (5) определяются энергетические потоки q , непосредственно зависящие от η :

lg q , = lg S i — ²⁰ lg h - lg

m ² n ²

, + - - 0,1 Lwc_ + 73, l12     l22            C

l ₁        l ₂

где L – октавные предельно допустимые уровни звуковой мощности, дБ.

C

Выводы. Изложенный подход позволяет решить задачу обеспечения санитарных норм шума при обработке ШСУ широкого класса деталей типа коробчатых оболочек при проектировании подобных технологических процессов.