О рассеянии звука на неупругом шаре произвольного радиуса. Фактор эффективности рассеяния

Теория рассеяния полей и частиц очень подробно разработана, и ее библиография насчитывает множество монографий и статей. Особенность теории рассеяния в том, что методы, разработанные в той или иной области ее применения, постепенно успешно востребуются в других ее областях. Такие термины, как "амплитуда рассеяния", "сечение рассеяния", "фактор эффективности рассеяния", "экстинкция", "оптическая теорема" и целый ряд других утвердились практически во всех подразделах теории рассеяния. Это позволяет говорить о теории рассеяния, как о единой теории, использующей сходные методы и в теории рассеяния волновых полей и в теории рассеяния частиц.

Ранее автор обращался к различным аспектам теории рассеяния (см., например, [1–5] и др.). Эта тема важна еще тем, что находит свое применение в различных прикладных задачах научного приборостроения, в частности, при расчете радиационного давления на одиночных частицах (см., например, [6–8]). Рассмотрение такой интегральной характеристики рассеянного поля, как фактор рассеяния, может существенно упростить изучение механизма силового воздействия звука не только на одиночные частицы, а и на их ансамбли.

Поле рассеяния неупругой сферы хорошо изучено. Так, еще в работе [9, §296], первое издание которой датируется 1879 г. рассматривается рассеяние плоской волны на жидкой сфере. В настоящей работе на примере расчета амплитуды акустического рассеяния на неупругом шаре применяется методика, принятая первоначально в квантовой механике (см., например, [10]), а затем рассчитывается фактор эффективности рассеяния этой сферы, принятый, например, в теории рассеяния света (см., например, [11–14] и др.).

ЦЕЛЬ РАБОТЫ

Целью работы является получение методами, принятыми в квантовой механике, аналитического выражения для амплитуды рассеяния с последующим получением выражения для сечения рассеяния шарика и тем самым выражения для фактора эффективности рассеяния, используемого, в частности, в теории Ми [15] рассеяния электромагнитных волн на однородном шаре.

АМПЛИТУДА РАССЕЯНИЯ НЕУПРУГОГО ШАРА

В задачах акустического рассеяния в качестве первичной волны рассматривается плоская волна единичной амплитуды и нулевой фазы в начале координат, куда помещен рассеиватель. Вследствие наличия включения возникает поле рассеяния, которое в сумме с первичным полем образует результирующее поле. Полагаем, что первичное поле характеризуется парой (v0, p0), рассеянное — парой (vs, ps), а суммарное (результирующее) поле — парой (v,p). Здесь v — вектор колебательной скорости; p — акустическое давление; индексы 0 и s характеризуют соответственно первичное и рассеянное поля; величины без индексов характеризуют результирующее поле. При этом подразумевается, что v = v0 + vs ,    P = P0 + Ps .

Задачу акустического рассеяния обычно рассматривают для случая идеальной жидкости в линейном приближении.

Пусть в жидкой среде, характеризуемой скоростью звука c и плотностью ρ , в начале координат расположен шарик радиусом a плотностью ρ ₁ и скоростью звука c ₁ . Заметим, что в жидкой среде эти два параметра среды полностью определяют ее свойства, принимаемые в линейной акустике — сжимаемость и плотность. Дальнейшее изложение будет основано на переложении в акустическую область соответствующих квантово-механических результатов [10].

Формализуем задачу. Пусть шар занимает область Q с центром в начале координат. Однородное пространство характеризуется парой ( р , c ) , однородный шар — тройкой чисел ( a , р 1 , с 1 ) . Тогда в случае гармонического поля с угловой частотой ω уравнение для звукового давления p запишется в виде (см., например, [1])

А p + к ² n ² ( r ) p = 0.                (1)

Здесь ( r ,0, ф ) — сферические координаты; к = го / c — волновое число среды; k , = го / с 1 — волновое число включения; n = c / c 1 — показатель преломления, в нашем случае

Г c / c 1 , r g [0, a );

n = <

[ 1,       r e ( a , да ).

Таким образом, внутри шара уравнение (1) запишется так

А p + k 1 ² p = 0 .

Первичная плоская волна имеет вид p ₀ = e ^{1 kz} , которая в разложении по сферическим функциям имеет вид [10, с. 222]

да p 0 = e • kz = e • krcos 0 =   £i l (2l +1) j 1 (kr) p (cos0),  (2)

kr I = 0

где j l ( kr ) — сферические функции Бесселя¹ ) (называемые также функциями Риккати—Бесселя) j l ( kr ) = ^Пnkr J l _{+ 1/2} ( kr ) ; J, _{+ 1/2} — цилиндрическая

функция Бесселя полуцелого порядка; Р_г ( cos 0 ) — полиномы Лежандра.

Найдем решение в области Q . Радиальная составляющая решения R ( kr ) в области Q подчиняется уравнению [16, с. 433]

1 d ( ₂ d R ) т-Я r -;-l ⁺ r d r I d r J

k ₁

—

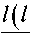
r ²

R = 0,

I = 0,1,2...

Конечное решение R_l ( kr ) в ограниченной об

ласти Q определяется в виде R_l ( k 1 r ) = = J _{l + 1/2} ( k r ) / ^k ^ r , где J _{l + 1/2} ( k , r ) — подчиняется

уравнению

d^{2 J} l + 1/2 ( ^k 1 r ) + 1 ^dJ l + 1/2 ( ^k 1 r ) + d r ²        r     d r

+

2_ ( I + 1/2 ) 2

1            „2

^dJ l + 1/2 ( ^k 1 r ) = ⁰.

В области Q по аналогии с анзацем (2) и с выражением в [10, с. 223] решение запишем в виде

¹⁾ Обычно сферические функции Бесселя определяются так (см., например, [16, с. 433]) j _l ( kr ) =

= V п /2 kr J _{l + 1/2} ( kr )

с асимптотикой lim ^j _l ( kr ) = kr ^да       '

= —sin kr —nn . Представленная выше в тексте kr (    2 J сферическая функция определена в [10] для удобства, т. к. при kr ^ да остается конечной с пределом

(     1     ^

Sin l kr — —nn I . Очевидно, что j _l ( kr ) = j _l ( kr ) / ( kr ) , и в этом случае (2) перепишется в виде p 0 = ]L i ^l ( 2 1 + 1 ) j _l ( kr ) P ( cos 0 ) , что касается и всех последующих разложений, где фигурирует агрегат ^j l ( ^kr ) / ⁽ kr ) .

1    ”

p=E i1 (21+0# j i (k r) Pi (cos6)= k 1 r 1=0

1 k

=, , E1 (21+1)ei j i (ki r) Pi (cos6), kr k 1 1=0

где β_l — константы, определяемые краевыми условиями задачи рассеяния.

Вне сферы О решение записывается [10, с. 223]

к функции j ₁ ( k ₁ r ) : L₁ =

f dlnj 1 ⁽ k 1 r ) ^

I . с введе dln r

V               / r=a нием Ll пропадает необходимость определения констант βl [10, с. 223], поскольку Ll от этих констант не зависят. После очевидных действий получаем

[ dln-j p l k L r ) I =f      jM ]

dln r ) j, (kr) d r x                  /r=a V J1 V 1 /               /r=(

1 ”

Р = Р 0 + P s = kr E l i ¹ ( ^{2 1 + 1} )

1 = 0

X

k1a j 1 (k 1a)

^j 1 ' ( ^k 1 ^a ) =

x ₁

^j 1 ( ^ 1 )

^j 1 ' ( ^ 1 ) ,

^X j 1 ^{( kr} ) + 2 « 1 h ^{( 1 ) ( kr} ) Pi ^{( c}os ⁶ ) , (3)

где p_s — давление в поле рассеяния; h ^{( 1 )} ( kr ) = ^Пnkr- H ⁽ + _1/2 ( kr ) — сферическая функция Риккати—Ханкеля первого рода;²⁾ α_l — искомые коэффициенты.

На границе шара r = а должны выполняться краевые условия для идеальной среды: равенство давлений на границе r = а — p|r = a = p| r = a и нормальных компонент скорости v l = v I , где r l r = a       г r- = а

• 1    д р     _     1 д р ,

• v, =-- , а v, =-- (это следует из урав-

• I®p дr         I®p1 дr

Sv        „ нения Эйлера р— = -Vр). Запишем эти условия. д t

Условие равенства давлений дает

• 1    = 0,1,2...,

где x ₁ = k₁ a , а j ₁ ' ( x ₁ ) означает производную по k ₁ r в точке х ₁ = k ₁ a . Разделив левую часть (5) на левую часть (4) (при этом β_l сокращаются),

1      Sj 1 (k 1r получаем              1

P1j 1 (k 1a)    д r действий получаем

. После очевидных

1       д j 1 ( k 1 r )      = k 1 a j 1 ' ( k 1 a ) =

P 1 j 1 ( k 1 a )     д r     r = _a    P 1 a j 1 ( k 1 a )    P 1 a

Окончательно после деления (5) на (4) получаем

k f

• ^в 1 j 1 ( ^k 1 a ) =—IJ 1 ( ^ka )

+— a, 2 ^l

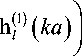
1 = 0,1,2,

...,

а условие равенства нормальных составляющих скоростей дает

± _e ⁵ J 1 ^{( k} 1 ^r ) P 1   ¹    д r

r = a

1 k ₁ ρk

д j ₁ ( kr )    1     д h ^{( 1 )}( kr )

д r     2 ¹    д r

r = a

1 = 0,1,2...

Введем, следуя [10, с. 223], обозначение логарифмической производной применительно

• ²⁾ См. предыдущую сноску по поводу функции j ₁ ( kr ) .

_p j 1 '⁽ x ^{) +} ^ « 1 ^{h ()} ' ^{( x} )

• L1    ( X 1 ) = x ^P^-------- 2----------- ,

^P j 1 ( ^x ) ⁺ ^ ^a 1 ^{h ( 1 )}( ^x )

• 1    = 0,1,2..., x = ka .

Здесь штрихи означают производную по kr . Из (6) получаем для α_l :

^x ~^j 1 ' ( ^x ) ^- L 1 ^j 1 ( ^x )

a ( x ) = 2--- ^р --------------=

• L 1    h ^{( 1 )}( x ) - x ^h ^{( 1 )} ' ( x )

L 1 ^j 1 ( ^x ) ^{- x} ~^j 1 '( ^x )

= - 2------------- P -------,            (7)

Li ^{h ( 1 )}( ^x ) ^{- x} ^ -h^{( 1 )} ' ( ^x )

1 = 0,1,2...

Вводя обозначение m =Pk для отношения плотности включения к плотности среды, получаем окончательно

( \ о LI ( x 1 )j 1 ( x )- xm j 1 '( x ) a l ( x ) = -2------—,,,    --------,,,     ,

L i ( x ) h ⁽⁾( x ) ^- xm h ⁽ ) ' ( x )

(7а)

1 = 0,1,2...

Из сравнения (2) и (3) определяется поле рассеяния

11 -to

Ps = ^K1 ( 21 + 1)ai h()( kr ) P ( cos 6 ).

² kr l = 0

Асимптотика функций h ^{( 1 )}( kr ) такова [10, с. 224]:

llmh(1)( kr ) = 1-(1+1)e1 kr.(9)

kr ^to' '

Подстановка (9) в (8) и выделение коэффици-eikr ента перед функцией дает выражение для ам-r плитуды рассеяния f (6) (см. [10, с. 224])

-to f (6) =    К21 + i^a.P. (cos6),          (10)

^{21 k} 1 = 0

все величины α_l в котором уже известны и приведены в (7).

Слагаемые ( 2 1 + 1 ) a l P ( cos 6 ) характеризуют мультиполи 1 -го порядка; например, 1 = 0,1,2 отвечают соответственно монополю, диполю и квадруполю. Приведем для 1 = 0,1,2 выражения P_t : P 0 = 1, P₁ = cos 6 , P ₂ = ( 3cos² 6 - 1 ) /2.

СЕЧЕНИЕ РАССЕЯНИЯ

Сечение рассеяния определяется отношением суммарного потока рассеянной звуковой энергии к интенсивности звука в падающей (первичной) волне. Найдем суммарный поток рассеянной звуковой энергии для рассматриваемого случая. Известно, что интенсивность или сила звука (как и интенсивность света) — это средняя по времени энергия, переносимая звуковой волной через единичную площадку, перпендикулярную к направлению распространения волны, в единицу времени. Для периодического звука усреднение производится либо за промежуток времени, больший по сравнению с периодом, либо за целое число периодов. Для плоской гармонической бегущей вол- p ²

ны интенсивность звука I равна I =J——, где 2ρc p — амплитуда звукового давления, ρc — волновое сопротивление среды [17, с. 159].

Согласно (8)–(10) имеем для давления поля e ikr рассеяния в дальней волновой зоне p s ~ f ( 6 )—. r

В дальней волновой зоне годится допущение о плоскости фронта волны, поэтому на сфере ра- p ² диуса r интенсивность I равна I s =^J—— = 2 ρc

=  ----2-.3) Тогда суммарный поток рассеянной

2 ρcr ²

звуковой энергии получается интегрированием Is по площади сферы S радиуса r j ^ 2 r2 sln 6 d6 d^ = — j|f (6)|2 sln6 d6.

Подставляя в последний интеграл выражение для f ( 6 ) из (10) имеем

π j|f(6 )|2 sin 6 d6 =

ρc ₀

1 π

4 k ² ρc

π j 0

to

E ( ² l ^{+ 1} ) ^a l P l ( ^{cos 6} )

l = 0

sin θ d θ .

Учитывая ортогональность полиномов Лежандра на интервале 6 е [ 0, п ] ,⁴⁾ получаем окончательно для суммарного потока рассеянной звуковой энергии

1 π

4 k ² ρc

π j 0

to

^ ( 2 1 + 1 ) a l P l ( cos 6 ) sln 6 d 6 = l = 0

1 π

4 k ² ρc

1 π

2 k ² ρc

to к 21+1)2 al r l=0

( ² l + ¹ )

to

к 21+1) al r.

l = 0

Интенсивность первичной волны I0 с учетом того, что амплитуда давления принималась p0 = 1

2 1 + 1,

(см. (2)), равна 1 0 = —^. Тогда сечение рассеяния

2ρc рассчитывается из отношения

1 π

2 k ² ρc

^ s ( x ) =

1 π

= 2 pc—-—

2 k ² ρc

to

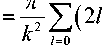
to

Z( 21 +1) W l=0

I 0

to

Z( 21 +1) к r l=0

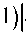
Приведем выражение (11) к размерности площади, которую имеет величина сечения рассеяния. Поскольку величины α_l , являющиеся функцией от x = ka , безразмерны (см. (7а)), то стоящая в (11) сумма также является безразмерной. Выражая в (11) к ² = x ² / a ², перепишем (11) в виде

Л 2 to

• ^- ( ^x ) = —Е ( ^{2 1 +} 1 ) к .       ^(11а)

x 1= 0

ПРИМЕРЫ РАСЧЕТА ФАКТОРА ЭФФЕКТИВНОСТИ РАССЕЯНИЯ

Ниже на рис. 1 и 2 представлены результаты расчетов фактора эффективности акустического рассеяния для двух жидких шаров, помещенных в воздушную среду. Параметры среды характеризуются скоростью звука с = 331м/с и плотностью р = 1 в относительных единицах (результирующие выражения зависят только от частного ρ / ρ ₁ , поэтому плотности можно задавать в относительных единицах); радиус шарика был принят a = 10 ^{- 4} м; скорость звука в материале шарика с 1 = 500 м/с; плотность шарика была принята р 1 = 1.1 (рис. 1) и р 1 = 1.5 (рис. 2). Результаты расчета фактора эффективности рассеяния K s ( x ) для обоих случаев представлены на рис. 1 и 2. На рис. 3 представлен пример из области рассеяния света на шарообразном включении (источник [11, с. 610]).

По оси абсцисс на всех рисунках отложен параметр Ми x = ka (на рис. 3 он обозначен через

В этом случае -_s ( x ) уже имеет размерность площади (величина x = ka также является безразмерной).

Функция фактора эффективности рассеяния

K_s = ^—Лт , принятая ранее в теории Ми, записыва- πa ²

ется в безразмерном виде

to

Ks (x) = "Л = -Z(21 +1)N         (12)

na    x i = o

и может использоваться и в звуковом рассеянии при оценке интегральных свойств рассеивателя. Как видно из (12), величина K s ( x ) >  0.

Таким образом, приведены точные выражения для оценки поля рассеяния на одиночном шарообразном включении при его облучении плоской гармонической звуковой волной. Следует ожидать, как и в случае рассеяния света, что результаты рассеяния на мелких нешарообразных включениях достаточно точно описываются приведенной теорией. Как и в случае рассеяния света, все приведенные выражения легко экстраполируются на случай наличия в первичном акустическом поле множества однотипных частиц. Так, если расстояния между шариками велики по сравнению с их радиусом, а локализованы они хаотично, то суммарная интенсивность рассеянного поля получается в виде суммы парциальных интенсивностей всех шариков (см. [18, c. 635] и др.).

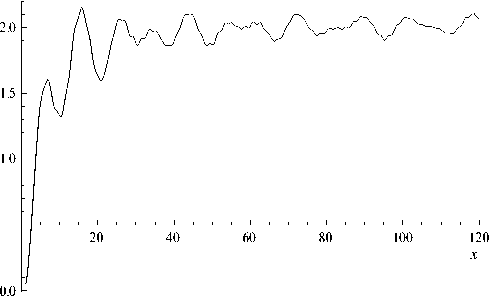
Рис. 1. Расчет фактора эффективности рассеяния для жидкого шарика с р 1 = 1.1

K S

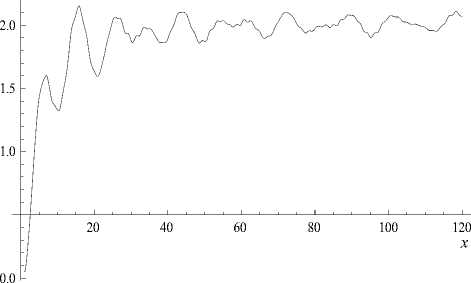
Рис. 2. Расчет фактора эффективности рассеяния для жидкого шарика с р 1 = 1.5

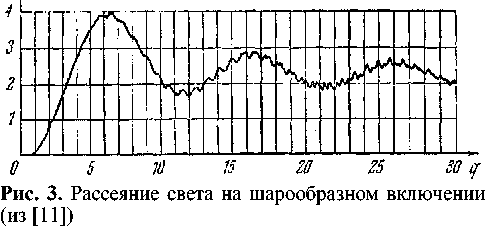
q ). По оси ординат представлены значения фактора эффективности рассеяния K s ( x ) . Отметим, что в электромагнитном случае вторым параметром, влияющим на поведение K s ( x ) является не отношение плотностей среды и шарика, а отношение показателей преломления среды и шарика.

Из рисунков видна схожесть поведения функции K s ( x ) в акустическом и оптическом случае. Кроме того, из рис. 1 и 2 видно, что возмущение плотности шарика на 36 % практически не ведет к возмущению функции K s ( x ) . При рассматриваемых параметрах видно, что графики асимптотически стремятся к постоянному значению K s ( x ) ~ 2. В области стабилизации кривой фактора эффективности рассеяния можно говорить о независимости интегральных рассеивающих свойств включения от частоты.

ВЫВОДЫ

В работе рассматривается рассеяние акустической волны на неупругом жидком шарике. Для вывода необходимых выражений используется математическая техника, применяемая в теории рассеяния частиц. Приводятся выражения для поля и амплитуды рассеяния шарика. Приводится адаптированный к акустическому случаю принятый в оптике интегральный параметр рассеивателя: фактор эффективности рассеяния, равный нормированному на геометрическое сечение включения отношению суммарного потока рассеянной звуковой энергии к интенсивности падающей на включение первичной волны. Приведены примеры расчета фактора эффективности рассеяния для конкретных параметров, которые сравниваются с оптическими аналогами. Полученные результаты для одиночного включения при определенных условиях легко распространяются на ансамбли множества частиц.