О расслоении полосы по границе раздела упругих свойств. Часть 1. Постановка задачи, случай нормального отрыва
Автор: Устинов К.Б.
Статья в выпуске: 4, 2015 года.
Бесплатный доступ
Рассмотрена задача о полосе, состоящей из двух изотропных упругих полос различной толщины, обладающих различными свойствами, разделенных полубесконечной трещиной, проходящей по границе раздела упругих свойств и нагружаемой на бесконечности системой усилий с ненулевым главным вектором и моментом. Путем применения преобразования Лапласа задача сведена к однородной матричной задаче Римана. В предположении возможности пренебрежения влиянием нормальных напряжений на сдвиговые смещения и сдвиговых напряжений на нормальные смещения задача сведена к двум скалярным задачам Римана. Данная постановка может рассматриваться как приближенная для общего случая (данное приближение при этом заведомо не хуже общепринятого приближения, заключающегося в рассмотрении узкого слоя в рамках теории балок либо стержней) и как точная - для случая, когда прилегающие слои могут скользить друг относительно друга, но удерживаются силами адгезии (например, вандерваальсовыми). Путем факторизации получено точное аналитическое решение одной из указанных задач, а именно задачи о нормальном отрыве. Получены асимптотические выражения для смещений берегов трещины вдали от ее вершины. Показано, что ведущие члены асимптотики смещений берегов трещины вдали от ее вершины соответствуют смещению балки при граничных условиях типа упругой заделки, т.е условиям пропорциональности смещения и угла поворота в точке заделки вектору усилия и изгибающему моменту посредством матрицы коэффициентов податливости.Для данных коэффициентов получены аналитические выражения. Также получены асимптотические выражения для поля напряжений вблизи вершины трещины (коэффициент интенсивности напряжений).
Тслоение, интерфейсная трещина, факторизация, упругая заделка
Короткий адрес: https://sciup.org/146211585
IDR: 146211585 | УДК: 593.3 | DOI: 10.15593/perm.mech/2015.4.13
Текст научной статьи О расслоении полосы по границе раздела упругих свойств. Часть 1. Постановка задачи, случай нормального отрыва
Задача продольного расслоения полосы, составленной из двух полос меньшей толщины, обладающих различными упругими свойствами, решалась многими авторами (например, [1-5]), при этом в основном интерес был сосредоточен на поведении решения вблизи вершины трещины. Однако в ряде задач, например при исследовании потери устойчивости отслаивающимися покрытиями, значение имеет поведение поля смещения вдали от вершины трещины [6-18]. Одной из наиболее простых конфигурация является полоса, составленная из двух полос меньшей толщины. Если длина отслоения много больше толщины полосы, для ряда случаев отслоение может рассматриваться как полу-бесконечное. Если толщина одного из слоев много больше протяженности отслоения, то такой слой может рассматриваться как полуплоскость; эффективное и элегантное решение задачи для такого случая, полученное путем применения преобразования Лапласа и сведения ее к матричной задаче Римана, было дано в работах [19-22] для одинаковых упругих свойств слоя и полуплоскости и в работе [17] для различающихся свойств. Ключевым моментом решения являлась факторизация матричного коэффициента. В указанных работах получены асимптотические представления для трансформант поля напряжений на линии продолжения трещины, и в конечном счете вычислены коэффициенты интенсивности напряжений (КИН) в зависимости от главных вектора и момента напряжений, действующих на продолжении трещины.
Однако интерес к задаче не ограничивается вычислением КИН. В частности, из указанного решения можно извлечь асимптотику смещений берегов трещины вдали от ее вершины [14]. При этом при наличии ненулевых главных вектора и момента действующих нагрузок ведущие члены асимптотики смещений берегов трещины будут, очевидно, соответствовать смещения балки (пластины), подверженной действию указанных главных вектора и момента при некоторых граничных условиях. Следует подчеркнуть, что эти граничные условия вовсе не являются условиями жесткой заделки. Они представляют собой [7, 10-15, 17] условия обобщенной упругой заделки, т.е. условия пропорциональности смещений и угла поворота в точке заделки действующим компонентам главных вектора и момента нагрузки. В работе [17] данное решение было обобщено на случай отслоения и основания, обладающих различными упругими свойствами, хотя и связанных некоторыми дополнительными ограничениями. В работе [16] рассматривалась возможность пренебрежения влиянием нормальных к линии трещины напряжений на сдвиговые компоненты смещения (и сдвиговых компонент напряжения на нормальные компоненты смещения), в результате было получено приближенное решение о сдвиговой трещине на границе раздела. Там же было показано, что подобное решение по крайней мере не хуже традиционного подхода - замены отслаивающейся части полосы одномерным объектом (стержнем). В настоящей статье рассматривается аналогичная задача для расслаиваемой составной полосы.
1. Общая постановка задачи о расслоении полосы, состоящей из двух упругих слоев по границе контакта
В условиях плоской деформации рассматривается неоднородная упругая полоса 1 < y < - h , составленная из двух изотропных частей с различными упругими свойствами, контакт которых проходит вдоль линии у = 0. Вдоль части границы у = 0, x < 0 имеется полный контакт, вдоль оставшейся части границы у = 0, x > 0 контакт отсутствует (рис. 1). Все величины, относящиеся к нижней полосе 1 < y < - h , будут обозначаться индексом 1, все величины, относящиеся к верхней полосе 0 < у < 1, индексом 2. Модули Юнга и коэффициенты Пуассона (модифицированные для условий плоской деформации) материалов полуплоскости и полосы обозначим E ( ' ) , v ( ' ) , i = 1,2 соответственно. С обычными модулями Юнга E 0 ( 1 ) и коэффициентами Пуассона v0( 1 ) они связаны соотношениями
Е * i 1 = E 0 ( ' * v* i ’ = V o< ' *
= ( 1 -V 0 ( i - )( 1 +v „ ( i > ) • = 1 -v „ ( i >-
В постановке плоской деформации рассматривается однородная задача: предполагается, что все поверхности свободны от напряжений,
°уу = °xy = 0, при y = 1, y = -h, и при y = 0, x > 0,(2)
а нагрузка с эквивалентными главным вектором ( T , N ) и моментом M приложена на бесконечности, так что
0 00
M = j x ° yy (x ,0) dx, N = j° yy (x ,0) dx, - T = j ° xy (x ,0) dx.(3)
-X -X-X
Условия сопряжения на границе имеют вид
О d)=G(2) f/1)^2)
° УУ ° УУ , ° xy ° xy ,
(1) (2) (1) (2) при У = О, x < 0.
u ’ = u < V - V 7
Здесь u , v - компоненты вектора смещения; о xx , о yy , о xy - компоненты тензора напряжений.
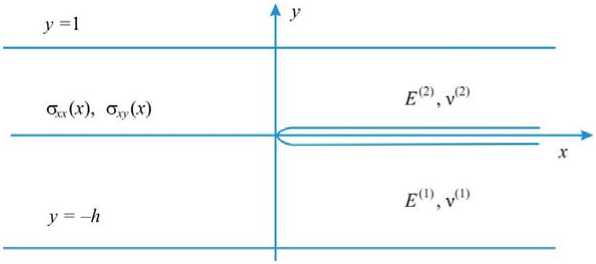
Рис. 1. Расслоение составного слоя. Геометрия задачи
В окрестности нуля поле напряжений должно быть интегрируемо.
° xy
= O (- x -v),
v< 1.
Из механики разрушения известно, что это поле имеет корневую особенность:
<
° уу
I
° xy
V-2 ax _ KII „
■ о(R ) .
Однако для построения решения можно довольствоваться условием (5), а условие (6) получится из решения. В случае различных значений упругих постоянных здесь могут присутствовать осциллирующие члены.
Воспользуемся результатами работы [22], в которой предлагается связь между образами двустороннего преобразования Лапласа от производной компонент вектора смещения to д
g(x' ) ( Р ) = i ^ U(' ) ( x ,0 ) e - P xdx , о x
-to
” я (7)
g У' ) ( p ) = J ^ v ( ' ) ( x ,0 ) e" p xdx о x
-to и напряжениями to
Q x ( P ) = J ° xy ( x ,0 ) e - P xdx ,
-to
to
Q y ( P ) = J ° УУ ( x ,0 ) e - P xdx
-to для полосы 0 < y < 1 (при поставленных граничных условиях свободной внешней границы оyy = оxy = 0, при y = 1). Вывод данных выражений дан в Приложении 1.
E (2)
gx2 (p) =
sin p cos p - p
d 2
qx (p)+dr^y( p )+
1 - v
- qy ( p ) ,
E (2)
gy2) (p) =
1 - v'
. (2)
- qx ( p )
^^^^^^^e
d 2 q x ( p )+
sin p cos p + p
d 2
p G L q y ( p ) ,
J 2 „ 2
d 2 = sin p - p .
Здесь L - мнимая ось.
Рассмотрим преобразование Лапласа от следующих величин:
Е (2) ОТ м p ) = —I 2 0
Л v <2) 5 x | u (2)
( x ,0 ) - v (1) ( x ,0 ) ( x ,0 ) - u (1) ( x ,0 )
\ e - px dx ,
F - ( p H
-от
° yy ( x ,0 ) °xy (x,0),
^ e - px dx .
Здесь использовано свойство равенства нулю скачка смещения для отрицательной полуоси и равенства нулю напряжений для положительной полуоси. На основании (4) подынтегральное выражение (11) тождественно равно нулю для x < 0, и, следовательно, F +( p ) аналитична в правой полуплоскости ( Re p > 0 ) . Аналогично согласно (2) подынтегральное выражение (12) равно нулю для x > 0 , и, следовательно, F _ ( p ) аналитична в левой полуплоскости ( Re p < 0 ) . Здесь аналогично [19-22] предполагается выполнение условия убывания напряжений на бесконечности при x ^ -от . В окрестности нуля выполняются условия (6). При x ^ +от смещения могут расти как полином третей степени (что соответствует ненулевой поперечной силе на бесконечности), следовательно, в Лаплас-образе F + ( p ) возможно появление полюса в нуле до третьего порядка включительно.
Комбинируя (7)-(12), получаем уравнение матричной задачи Римана, аналогичное [19-22]:
F+ (p ) = К (p) F (p), где
К (p ) = ( a11 a121, p g L, у a21 a22 J a11 =(sinpcosp + p)/d2 +p(sinhp coshp + hp)/d1, a12 =-а2i =-p2 /d2 +p(hp)2 / d1 -P'/2, a22 =(sinpcosp -p) / d2 +p(sinhp coshp-hp) / d1,
d1 - sin2 (hp)-(hp)2, d2 - sin2 p -p2,(16)
ц = E(2) / E(1), p' -1 -v(2)-p(1 -v(1)).(18)
Основная сложность состоит в факторизации матричного коэффициента K ( p ) , т.е. в представлении его в виде
K (p)-X+ (p) X-1 (p),(19)
где функции X± ( p ) аналитичны в правой и левой полуплоскости комплексного переменного р . det X± ( p ) * 0 в соответствующих плоскостях вплоть до границы. В настоящее время общее точное аналитическое решение указанной задачи неизвестно; можно указать несколько путей построения решения:
-
- применение аппроксимаций для матричного коэффициента (14) задачи методами [23-26];
-
- построение приближенных решений в предположении возможностью пренебречь перекрестными членами в (14) (положить a12 - a 21 - 0) [16];
-
- построение решения для частных случаев, для которых факторизация может быть осуществлена [27-34].
-
2. Задача о трещине нормального отрыва. Постановка
Далее решение будет получено с использованием второго из указанных методов.
С помощью предположения о возможности пренебрежения в (14) влиянием перекрестных членов, что соответствует a 12 - — a 21 - 0, матричная задача распадается на две скалярные. Данное приближение заведомо не хуже традиционной замены слоя однородным объектом - стержнем либо балкой [35-37]. Рассмотрим задачу о нормальном отрыве.
F+( p)-K (p) F— (p), p G L,(20)
P (2) m
F+ (p) = — j — [ v(2) (x,0)- v(1) (x,0)] e " pxdx,
F- (p )=]a „ (x ,0) e- pd,(22)
-TO
K ( p ) - ( sin p cos p + p ) / d 2 + p ( sin hp cos hp + hp ) / d 1, d 1 - sin2 ( hp ) - ( hp ) 2, d 2 - sin2 p - p 2.
Аналог (19) становится скалярным уравнением
K ( p ) = Л - 1 ( p )ЛД p ) . (24)
После нахождения Л ± ( p ) окончательное решение дается с помощью теоремы Лиувилля
F + ( p ) = Л + ( p ) n ( p ) , Re ( p ) >0,
F-( p ) = Л_( p )П( p), Re (p )< 0.
Здесь П ( p ) - функция, подлежащая определению.
Второе из уравнений (3) и условия (6) для интересующих нас величин после трансформации принимают соответственно вид
F-(p) = N + Mp + o(p), Rep ^0-.
F -( p I
K + O ( p 3/2), Re p ^ -да.
-Эи v /
Из элементарных соображений также следует, что производные от нормальных смещения для нижней кромки верхней полосы при x ^ да будут расти как ( 12 Mx - 6 Nx 2 ) / E (2), а нижней - как - ( 12 Mx - 6 Nx 2 ) / ( hE (1) ) , что в Лаплас-образах согласно (17)даст
F+(p) = 6(1 + П/h3)| M x 7 ( p
N p )
+ o ( p 2 ) , Re p ^ 0 +.
Условие отсутствия скачка смещений в нуле в трансформантах записывается следующим образом
F + ( p ) = O ( p - k ) ,
Re p ^ -да .
Данные условия будут использованы для определения П ( p ) .
-
3. Решение задачи Римана
Уравнения (23) могут быть записаны в виде (здесь L - мнимая ось)
Л- 1 ( p ) Л + ( p ) = ( 1 + Д ) Ctg3 p G 2 ( p ) , p G L ,
G2 (p ) = , 1 tg3 p 1 + p
sin p cos p + p sin hp cos hp + hp
2 2 ^ - 2 , Z, x2
sin p - p sin hp - ( hp )
, p G L .
С помощью стандартного приема факторизации арктангенса через гамма-функцию решение может быть выражено следующим образом:
Л+( p ) = л/1 + П
Г3 (1 + p / л) , .
J 2+ ( p ) ,
Г ( 1/2 + p / л )
Л-( p) =
1 Ht/i-^
, Г3 (- p / л) J2-( pJ ’
J2±( p ) = exp <
2 л _ю
th
+
sh 5 ch 5 + 5 sh hs ch hs + hs sh2 s - s 2 sh2 hs - ( hs )2
ds is - p
Для получения решения осталось определить функцию П ( p ) , число независимых параметров в которой определяется индексом задачи и поведением решения в опорных точках. Наличие опорных точек только в нуле и на бесконечности определяет вид П ( p ) как сумму слагаемых с положительными и отрицательными степенями р . Более детальное исследование показывает, что наиболее общим видом является
П( p )=
Здесь D2,D3 - постоянные, определяемые из граничных условий. Наличие членов со степенями p большими минус двух привело бы к нарушению условия (29), а меньшими минус трех - к нарушению условия (28).
Для определения постоянных D 2, D 3 потребуется разложение функции Л +( p ) вблизи нуля (два члена). Однако для определения параметров упругой заделки необходимо четыре члена. Для внеинтегрального члена (32) имеем
Г3 ( 1 + p / л )
Г3 ( 1/2 + p / л )
= 7i+n л ул
61п2
—— p + л
181n22 л2
1 2
- p +
6 [ 6 1п32-ф ) ] 3ln2
л3
л
p 3 + О ( p *).
Здесь £ ( x ) - дзета-функция Римана, ^ ( 3 ) ~ 1,20206.
Для интегрального члена (32) из (34), (97), (101), (103), положив
t = is , имеем
J 2+ ( p ) = h 11,2 ( 0 ) 11 + / 1 p +1 1 1 2 + 1 1
h (s) = ——th3 s
V ’ 1 + p
sh s ch s + s sh hs ch hs + hs sh2 s - s 2 ^ sh2 hs - ( hs )2
6 (p + h3) h ( 0 ) = 4 f
p 3 > + О ( p 4 ) ,
1 = 1 rd Inh (s) ds = 1 rh'(s) ds = 1 r h (s) ds 1 2л ^ ds s 2л ^ h (s) s 2л ^ h (0) ss1’ h" (0) 2 (5q-q h2 + 4 h3)
2 h (0) 5 (p + h3)
1 rd 3 In h ( s ) ds = 1
h'" (s)
ds 3
s 2л J ^ h(s)
^^^^^^^s
3 hvys, + 2 h ( s )
h'3 (s)) ds
h 3 ( s ) J
s
Выражение для интеграла I 1 (40) можно преобразовать следующим образом:
1 to
th s 1 3
s
ds s2
to
th s ds
to
3 г . th s ds 3 r 1
2 л J s s 2 л J sh s
-to
s
-to L
1 ds
^^^^^^^s ^^^^^^^^^
s
s
to
=6 z л n .1
( - 1) n 6ln2
^^^^^^^s
n
л
из (40), (38), (43) следует
6ln2
1 A
л
I
1A =
= 1 dd In h A ( s ) ds = 1 hhA '( s ) ds = 1 r 2 лJ
ds
s 2л J hA (s) s
h A ( s ) ds
Ы0) s 2’
hA(s> =1+0
s 3
sh s ch s + s sh hs ch hs + hs sh2 s - s 2 ^ sh2 hs - ( hs )2
Подстановка выражения для функции П ( p ) (35) и разложения вблизи нуля функции Л +( p ) (результата подстановки (36)-(39) в (32)) в первое из равенств (25) дает разложение Лаплас-образа производной от скачка смещения вблизи нуля. С точностью до двух ведущих членов оно имеет вид
F + ( p ) = D ^^ЕШ + ^^^ / p/h l ^ D л + d 3 ( л 1 1 + 6 in2 )p o ( p -^ ) , Re p ^ 0 + . (47)
Сравнение (47) с (28) позволяет вычислить значение констант, входящих в П ( p ):
D2 = л/бл ^/1 + р/h3 ^лM + (л11 + 6ln 2)N],
D 3 = -л3 / 2 V6д/1 + 0 / h3N -
Таким образом, задача решена: подстановка значений констант (48) в (35), а затем вместе с (32)-(34) в (25) дает Лаплас-образы напряжений и производной от разности смещений вдоль границы раздела упругих свойств.
-
4. Определение асимптотики смещения берегов разреза вдали от вершины трещины
Лаплас-образ указанной асимптотики может быть получен путем подстановки (48), (35), (32), (36)-(39) в (25). Результат данной подстановки может быть записан в виде
F +( p ) = 6 ( 1 + о/ h 3) f M - N )+ K u M M + K u N N + KuMM + K u N N + O ( p ) , Re p ^0 +. (49)
X ’ V p p J 2 p
K u m = 12 ( 1 + 0 / h 3 ) | I 1 +
6ln 2 ) 3
1 = 12 ( 1 + 0 / h ) 1 1 A • л J x '
- u N
K , „ = 6 ( 1 + ц / h 3 ) 1
uM
= 6 (1 + ц / h3)
= 2 (1 + ц / h3)
^^^^^B
6ln2
К
6ln2
К
36^(3)
6ln2
К 3
К
= 6 ( 1 + ц / h 3 ) 1
= 6 (1 + ц / h3)
= 2 (1 + ц / h3)
^^^^^B
- -2+1
1 A
1 + ~ + 11A
36^(3)
К 3
+ 2 1 1 A
Первый член в (49) соответствует прогибу балки, нагружаемой силой и моментом. Оставшиеся члены могут интерпретироваться как поправки к элементарной балочной теории (типа модели балки Тимошенко, учитывающей вклад в смещения от поперечной силы) и дополнительные смещения, вызываемые граничными условиями, отличающимися от условий жесткой заделки. Величины, определяемые формулами (50)-(53), являются при этом коэффициентами пропорциональности между поперечной силой и моментом, с одной стороны, и углом поворота и нормальным смещением - с другой.
Поскольку из приведенного решения непосредственно невозможно выделить указанные причины и при этом естественно ожидать, что матрица податливости должна быть симметрична, для модели эквивалентной балки естественно принять граничное условие в симметричном виде:
K u N = K ,M = 6 ( 1 + 1 / h 3 ) 1 , A \ (54)
Зависимость Ku M от h для различных отношений модулей представлена на рис. 2.
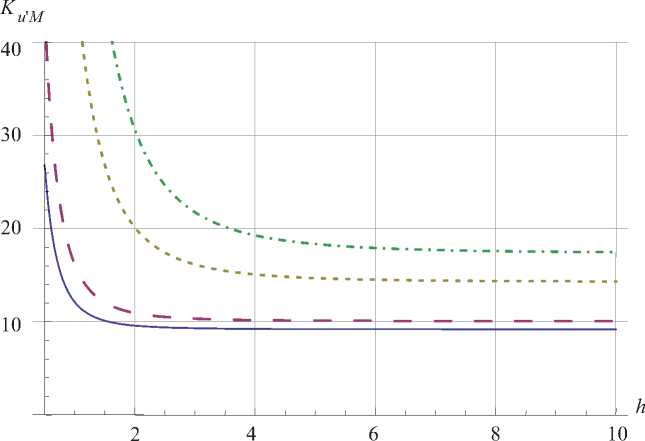
Рис. 2. Зависимость коэффициента упругой заделки Ku M от относительной толщины основания h для различных отношений модулей: сплошная линия - ц = 0,5 ; пунктирная - ц = 1; точечная - ц = 5 ; штрих-пунктирная - ц = 10
Для толстых оснований ( h ^ x ) справедлива асимптотика
hA ( s ) =
sh s ch s + s
1 + pL sh2 s - ss'
+ 2p
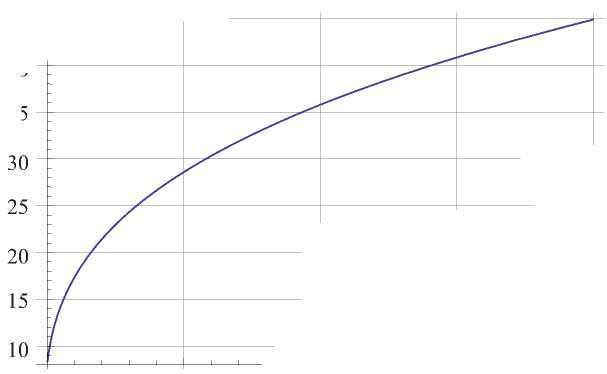
Здесь 1 1 A по-прежнему определяется (45). Зависимость Ku M от отношения модулей р для больших h ( h ^да ) представлена на рис. 3. Данная зависимость неплохо аппроксимируется формулой
K u M = 1 + 7,5р1/3.
K u ' М
П
Рис. 3. Зависимость коэффициента упругой заделки Ku M от отношения модулей р для больших толщин подложек ( h ^да )
-
5. Определение параметров разрушения
При p ^ -да для (33) справедливо следующее асимптотическое разложение:
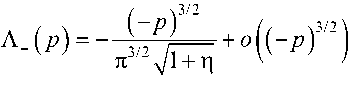
( Р )
+ р
Подстановка (58), (35), (48) в (25) и разложение для больших отрицательных p ^ -да дает
F-(p) = Тб71 +р/А3 [м +11 an]+o(-p.„=). V - p 71+р х 7
Последнее выражение немедленно дает асимптотику напряжений при x ^ - 0
л| х | 71 + р
[ M + 1 1 A N ] + o (| x -1'2).
Отсюда КИН
Ki = №п/h3 [м +11 an].
1 +п
Скорость высвобождения энергии [38, 39] при этом имеет вид
-
(1) (2) 6 (1 + р / h3),
J = K/ E m т = K(M + I^N)2.(62)
-
1 2E(1)E(2) 1 2E(2) E^)
Полученное выражение для скорости высвобождения энергии для р = 1, h = 1 совпадает с элементарным решением (например, [2]). При рассмотрении задачи о распространении интерфейсной трещины в классической постановке приведенный анализ для определения параметров разрушения может рассматриваться лишь как приближенный, поскольку в общем случае в точном решении будут присутствовать обе моды. Однако задача имеет и самостоятельное значение [13] для случая, когда прилегающие слои могут скользить друг относительно друга, но удерживаются силами адгезии (например, вандер-ваальсовыми).
Заключение
Получено и исследовано решение однородной задачи о полубесконечной трещине, проходящей вдоль границы, разделяющей два упругих слоя с отличающимися свойствами. Путем применения преобразования Лапласа задача сведена к однородной матричной задаче Римана. В предположении возможности пренебрежения влиянием нормальных напряжений на сдвиговые смещения и сдвиговых напряжений на нормальные смещения задача сведена к двум скалярным задачам Римана. Получена асимптотика поля напряжений вблизи вершины трещины, имеющего корневую особенность при отсутствии осциллирующих членов. Посчитан коэффициент интенсивности напряжений. Показано, что ведущие члены асимптотики смещений берегов трещины вдали от вершины трещины соответствуют смещению балки при граничных условиях типа упругой заделки, то есть условиях пропорциональности смещения в точке заделки вектору усилия и изгибающему моменту.
Работа выполнена при финансовой поддержке Программы Президиума РАН № I.3.
Приложение 1. Вывод связи между производной от скачка смещения и напряжениями на границе слоя
Рассмотрим плоскодеформированное состояние полосы у е [0,1] в декартовой системе координат, верхняя граница у = 1 которой свободна от напряжений.
° уу ( х ,1 ) = ° xy ( x ,1 ) = 0, (63)
а к нижней границе у = 0 приложена некоторая система нагрузок
° ху ( Х ,0 ) = Ч х ( Х ) , (64)
о yy ( x ,0 ) = q y ( x ) .
Здесь qx ( x ) , q y ( x ) - заданные функции. В основном изложение следует работам [19-22].
Найдем связь между действующей на нижней границе полосы системой нагрузок и производными от компонент смещений — ( x ,0 ) , — ( x ,0 ) .
Эx
Полная система уравнений теории упругости включает:
-
1) уравнения равновесия в отсутствие объемных сил
Эо , Э° xy
— -
Эx
Эо Эо xy । yy _ о
Эx Эy’ где оxx, оyy, оxy - компоненты тензора напряжений;
-
2) уравнения закона Гука, выраженные через компоненты смещений u , v:
E<2) ЭХ "(о xx+ о yyИ1+ v'2))о yy ’
E с) rsu -Sv У 2(1 .., ,,(69)
(эу Эх J V ' xy где E|2), v|2) - модуль Юнга и коэффициент Пуассона полосы;
-
3) уравнение совместности, выраженное через компоненты тензора напряжений
( a2 a2 Y
-
- (о -о I 0. (70)
(Э х 2 Э у 2 JV xx yy)
Для решения поставленной задачи подвергнем уравнение (69) следующим преобра-
Э u зованиям. Подставим значение из уравнения (68) в продифференцированное по x
Э x уравнение (69).
E <2- v _ ( 1 -v (2> ) f 2 ''-^ У(о - + о уу ) . (71)
Э x 2 а Э x Э y J Э у
Подстановка сюда уравнений равновесия (67) дает
-
E (2) Э 2 ; _ ( 1 + v (2) ) Эо У Г _ Э(о хх +о уу ) . (72)
Э x 2 Э y Э y
Для решения системы уравнений (66), (67), (68), (72), (70) используем двустороннее преобразование Лапласа, определяющее образ f ( p ) функции f ( x , y ) ,
№
/ ( Р , У ) = f f ( х , У ) e - px dx • (73)
—№
Обратное преобразование при этом определяется как f (х, У ) = - 1-7 f f (Р, У) е^Р, (74)
2k г где направление обхода по контуру L, соответствующему мнимой оси, осуществляется сверху вниз.
Трансформанты от уравнений (66), (67), (68), (72), (70) и граничных условий (63), (64), (65) примут вид
-
- ( v d 6 ху ( Р , У )
Р6хх ( Р, У ) +---5---- - 0
dy
-
, / х d 6 УУ ( Р , У )
Р6ХУ (Р, У) +—----- 0,(76)
dy
( . d 2 V
Р + "ТГ [6ХХ (Р, У ) + 6УУ ( Р, У )]- 0,
-
V dy 7
Е(2)й'(Р,У) = 6хх (Р,У) + 6УУ (Р,У)-(1 + v(2))аУУ (Р,У),
РЕ(2) V' ( Р, У ) = Р (- + v(2) )6 хх ( Р, У )- ^У [(J хх ( Р, У ) + 6 УУ ( Р, У )],
6ху (Р,-)^6УУ (Р,-)^ 0,
6ху (Р,0) = Чх (Р) ,
6уу (Р,0)^ Чу (Р) •
Здесь
, 5 й , 5 v й' - —, v ' = —,(83)
5х5
а
№
Ч х ( Р ) = f 6 ху ( х ,0 ) e - РхУх ,
-№
№ (84)
Чу (Р)= f 6уу (х,0)e-РхУх -№ есть трансформанты от напряжений на нижней границе.
Решение системы обыкновенных дифференциальных уравнений (75)-(79) с граничными условиями (80)-(82) дает выражения для трансформант производных смещения через действующие на нижнем крае полосы ( у - 0 ) напряжения. Для поставленной задачи интерес представляют значения трансформант производных смещения на этой же линии ( у - 0 ) :
g X 2) ( p ) = Sin p C O S p - p q x ( p ) + p_ q y ( p )+ l-^ q y ( p ) ,
-
E, g™ ( p )-1: q. ( p )-^ qx ( p )+sm pco; p+p qy ( p ),
2 2 dd d = sin2 p - p2.
Здесь to Д g.2) ( p )= J - u (x,0 )e- pxdx, ox
-to
- . (87)
g y 2) ( P ) = / ~ v ( x ,0 ) e - pxdx .
o x
-to
Коэффициенты в полученных выражениях аналитичны на всей мнимой оси за исключением нуля, где они имеют полюса до третьего порядка включительно. Полюс третьего порядка в нуле трансформанты соответствует квадратичному росту оригинала на бесконечности. Следовательно, из полученных выражений, в частности, следует, что при отсутствии особенностей для напряжений производные от смещения могут расти как квадрат расстояния, а сами смещения как куб расстояния. Для полосы такое поведение является общеизвестным фактом, в частности, в рамках элементарной балочной теории, являющейся при определенных условиях строгой асимптотикой точной теории, смещения вдали от приложенной системы сил с ненулевым главным вектором растут как третья степень расстояния.
Приложение 2. Разложение факторизующих функций вблизи нуля
Пусть существует факторизация функции h ( t )
h ( t ) = H + ( z ) / H _ ( z ) , (88)
H + ( z ) = exp—— j —— dt . (89)
-
x ' 2л iJ t - z
Пусть функция h ( t ) четная h ( - t ) = h ( t ) . Тогда функция In h ( t ) тоже четная. Согласно формулам Сохоцкого-Племеля предельные значения H ± ( 1 0 ) выражаются следующим образом:
ln H + ( t о ) - ln H - ( t о ) = In h ( t о ) , (90)
, . , . 1 In h ( t )
In H +( 1 0 ) + In H -( 1 0 ) = — J dt . (91)
л i t — 1 0
Из последнего равенства с учетом четности ln h ( t ) для 1 0 = 0 следует ln H + ( 0 ) = - ln H - ( 0 ) . Подставляя полученное равенство в (90), получаем
H 0 1 = H , ( 0 ) = h 11,2 ( 0 ) .
Для получения следующих членов разложения вычислим k -ю логарифмическую производную от обеих частей равенства (88):
ln H ( z ) -—г-ln H ( z ) = —-т-ln h ( z ) . (93)
dzk + ( ) dzk - ( ) dzk ( )
На основании формул Сохоцкого-Племеля предельные значения функций dk ln H (z) в нуле следующие:
dzk ■ ' -
dk , .1
— ln H i( z ) = 1- — ln h ( z )-Ik, dz2
I = 1 dk ln h (t) dt k 2лi dtkt ’
причем если функция h ( t ) четная, то для всех нечетных k в правой части равенства (94) будут обнуляться первые члены, а для всех четных k - вторые.
Выпишем несколько первых членов получаемого таким образом разложения. Для первой логарифмической производной
H -'(0) = H -'(0) = I H -(0) H -(0)'■
, 1 rdlnh(t) dt 1 th'(t) dt 1
1 1 = = = ln h ( t ) ^.
2лiJ dt t 2лi1 h (t) t 2лiJt
Для второй логарифмической производной
H 1 ' ( 0 ) - H '1 2 ( 0 ) = 1 у(0)
H 1 ( 0 ) H ± 2 ( 0 ) 2 h ( 0 ) .
С учетом (96) данное выражение преобразуется к виду
H 1 " ( 0 ) =1 h " ( 0 ) . I 2
H 1 ( 0 ) 2 h ( 0 ) 1.
Для третьей производной получаем
H 1 " ( 0 ) - 3 H '1 ( 0 ) H 1 " ( 0 ) . 2 H V ( 0 ) = I
H 1 ( 0 ) H 1 2 ( 0 ) H 1 3 ( 0 ) ;
I = 1 . d 3 ln h ( t ) dt
3 2 л i dt3 t
J 2 л i
^ h "' ( t ) V h ( t )
h' (t)h" (t) h2 (t)
2 h'3 (t)) d£ h3 (t )Jt•
С учетом (96) и (99) выражение (100) преобразуется к виду
H1" (0) = I + 3 h" (0) I + I з
H ± ( 0 ) 3 2 h ( 0 ) 1 1
В результате для разложения факторизующих функций вблизи нуля может использоваться следующее представление:
h" (0)
H (z ) = h+1/2 (0)< 1 + Iz + — + + V ’ V J 12 [ 2h (0)
2 1
z + —
. + 3 h "( 0 ) 3 2 h ( 0 )
3 z
+ O ( z 4 ) .(103)
Данный вывод не представляет сложности, однако в литературе (например, [40, 41]) обычно ограничиваются лишь двумя членами разложения.
Список литературы О расслоении полосы по границе раздела упругих свойств. Часть 1. Постановка задачи, случай нормального отрыва
- Suo Z., Hutchinson J.W. Interface crack between two elastic layers//Int. J. Fract. -1990. -Vol. 43. -Р. 1-18.
- Hutchinson J.W., Suo Z. Mixed Mode Cracking in Layered Materials//Adv. Appl. Mech./eds. J.W. Hutchinson, T.Y. Wu. -1992. -Vol. 29. -Р. 63-191.
- Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. -М.: Наука. 1983. -487 с.
- Григолюк Э.И., Толкачев В.М. Контактные задачи теории пластин и оболочек. -М.: Машиностроение. -1980. -415 с.
- Греков М.А. Сингулярная плоская задача теории упругости. -СПб.: Изд-во С.-Петерб. ун-та, 2001. -192 с.
- Ustinov K.B., Dyskin A.V., Germanovich L.N. Asymptotic analysis of extensive crack growth parallel to free boundary//3rd Int. Conf. Localized Damage -94. -1994. -Р. 623-630.
- Cotterell B., Chen Z. Buckling and cracking of thin film on compliant substrates under compression//Int. J. Frac. -2000. -Vol. 104. -No. 2. -P. 169-179.
- Dyskin A.V., Germanovich L.N., Ustinov K.B. Asymptotic analysis of crack interaction with free boundary//Int. J. Solids Structures. -2000. -Vol. 37. -P. 857-886.
- Yu H.H., He M.Y., Hutchinson J.W. Edge effects in thin film delamination//Acta Mater. -2001. -Vol. 49. -P. 93-107.
- Yu H.-H., Hutchinson J.W. Influence of substrate compliance on buckling delamination of thin films//Int. J. Fract. -2002. -Vol. 113. -P. 39-55.
- Effect of substrate compliance on the global unilateral post-buckling of coatings: AFM observation and finite element calculations/G. Parry, J. Colin, C. Coupeau, F. Foucher, A. Cimetière, J. Grilhé//Acta materialia. -2005. -Vol. 53. -P. 441-447.
- Гольдштейн Р.В., Устинов К.Б., Ченцов А.В. Оценка влияния податливости подложки на напряжения потери устойчивости отслоившегося покрытия//Вычисл. мех. спл. сред. -2011. -Т. 4, № 3. -С. 48-57.
- Салганик Р.Л., Устинов К.Б. Задача об упруго заделанной пластине, моделирующей частично отслоившееся от подложки покрытие (плоская деформация)//Известия РАН МТТ. -2012. -№ 4. -C. 50-62.
- Устинов К.Б. Еще раз к задаче о полуплоскости, ослабленной полубесконечной трещиной, параллельной границе//Вестник ПНИПУ. Механика. -2013. -№ 4. -C. 138-168.
- Ustinov K.B. On influence of substrate compliance on delamination and buckling of coatings//Eng. Fail. Analys. -2015. -Vol. 48B. -Р. 338-344.
- Устинов К.Б. О сдвиговом отслоении тонкой полосы от полуплоскости//Изв. РАН. МТТ. -2014. -№ 6. -С. 141-152.
- Устинов К.Б. Об отслоении слоя от полуплоскости; условия упругой заделки для пластины, эквивалентной слою//Изв. РАН. МТТ. -2015. -№ 1. -С. 75-95.
- Устинов К.Б., Каспарова Е.А. Оценка влияния кривизны и податливости основания на параметры отслоения покрытия//Деформация и разрушение материалов. -2015. -№ 3 -С. 28-35.
- Златин А.Н., Храпков A.A. Полубесконечная трещина, параллельная границе упругой полуплоскости//Докл. АН СССР. -1986. -Т. 31. -С. 1009-1010.
- Златин А.Н., Храпков A.A. Упругая полуплоскость, ослабленная трещиной, параллельной ее границе//Исследования по упругости и пластичности. Проблемы современной механики разрушения. -1990. -T. 16. -С. 68-75.
- Златин А.Н., Храпков A.A. Векторная задача Римана с ненулевым индексом показателя матрицы-коэффициента//Изв. ВНИИГ им. Б.Е. Веденеева. -1985. -Т. 181. -С. 12-16.
- Khrapkov A.A. Wiener-Hopf method in mixed elasticity theory problems. -S.-P., 2001.
- Ворович И.И., Александров В.М., Бабешко В.А. Неклассические смешанные задачи теории упругости. -М.: Наука, 1974. -456 с.
- Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. -М., 1979. -320 с.
- Бабешко В.А. Обобщенный метод факторизации в пространственных динамических смешанных задачах теории упругости. -М.: Наука, 1984. -256 с.
- Abrahams I.D. On the non-commutative of factorization of Wienner-Hopf kernels of Khrapkov type//Proc. Roy. Soc. London A. -1998. -Vol. 454. -Р. 1719-1743.
- Heins A.E. System of Wiener-Hopf equations//Proceeding of Symposia in Applied mathematics II. -McGraw-Hill, 1950. -Р. 76-81.
- Чеботарев Г.Н., К решению в замкнутой форме краевой задачи Римана для систем n пар функций//Учен. зап. Казан. ун-та. -1956. -T. 116б. -Kн. 4. -С. 31-58.
- Daniele V.G. On the factorization of Wiener-Hopf matrices in problem solvable with Hurd’s method//Trans ANTENNAS propagate. -1978. -Vol. 26. -Р. 614-616.
- Jones D.S. Commutative Wiener-Hopf factorization of a matrix//Proc. R. Soc. A. -1984. -Vol. 393. -Р. 185-192.
- Моисеев Н.Г. О факторизации матриц-функций специального вида//Докл. АН СССР. -1989. -Т. 305, № 1. -C. 44-47.
- Antipov Y.A., Moiseev N.G. Exact solution of the plane problem for a composite plane with a cut across the boundary between two media//J. Appl. Math. Mech. -1991. -Vol. 55. -Р. 531-539.
- Antipov D.A., Silvestrov V.V. Factorization on a Riemann surface in scuttering theory//QR. J. Mech. Appl. Math. -2002. -Vol. 55. -Р. 607-654.
- Antipov D.A., Silvestrov V.V. Vector functional difference equation in electromagnetic scuttering//IMA J. Appl. Math. -2004. -Vol. 69. -No. 1. -Р. 27-69.
- Koiter W.T. On the diffusion of load from a stiffener into a sheet//Quart. J. Mech. Appl. Math. -1955. -Vol. 8. -Part 2. -P. 164-178.
- Alblas J.B., Kuypers W.J.J. On the diffusion of load from a stiffener into an infinite wedge-shaped plate//Applied Scientific Research, Section A. -1965-1966. -Vol. 15. -Iss. 1. -P. 429-439.
- Каландия А.И. Математические методы двумерной упругости. -М. Наука, 1973. -303 с.
- Салганик Р.Л. О хрупком разрушении склеенных тел//ПММ. -1963. -Т. 27. -№ 5. -C. 957-962.
- Malyshev B.M., Salganik R.L. The strength of adhesive joints using the theory of crack//Int. J. Fract. Mech. -1965. -Vol. 1. -No. 2. -C. 114-128.
- Мусхелишвили Н.И. Сингулярные интегральные уравнения. -2-е изд. -М.: Наука, 1962. -600 с.
- Гахов Ф.Д. Краевые задачи. -М.: Наука, 1977. -640 с.


