О размерности границ некоторых фрактальных множеств на гексагональных решётках

Начиная с основополагающих работ Б. Мандельброта [1–4], который ввёл в научный обиход понятие фрактальной геометрии, аппроксимационные модели, использующие фрактальные объекты, стали широко применяться в различных областях естествознания [5–7].

В работе [8] показана самоподобность объектов, исследуемых в нанофотонике, и перспективная возможность использования фрактальных моделей для их исследования. Следует отметить, что плоский характер отображения наблюдаемых в нанофотонике изображений, его самоподобные фрактальные свойства диктуют необходимость исследования изображения как некоторой области плоскости, так и отдельно его границы. Необходимость исследования границы фрактального объекта в приложениях может объясняться, например, тем, что при решении задач, использующих, в частности, метод Монте–Карло и его разновидности, уже нельзя считать, что граница объекта имеет меру Лебега, равную нулю. С этой точки зрения исследование различных частных случаев граничных свойств специфичных фрактальных объектов представляется весьма актуальной задачей. В частности, В. Джильберт в работах [9, 10] исследовал фрактальную размерность границы фундаментальной области канонических систем счисления. В этих работах В. Джильбертом была указана явная связь между свойствами границ различных фракталов и представлением комплексных чисел в соответствующих канонических системах счисления. Дж. Тусвальднер в своей работе обобщил результат В. Джильберта на случай мнимых квадратичных полей [11], а затем и на случай двумерных канонических систем счисления [12].

В цитируемых работах рассматривается случай прямоугольных, точнее параллелепипедальных решёток, элементами которых являются целые элементы рассматриваемых квадратичных полей, однако значительная часть реальных кристаллов имеет не параллелепипедальную структуру, а гексагональную [13, 14]. Следы (изображения) таких гексагональных структур явно прослеживаются при наблюдении наноструктур, в частности, посредством различных регистрирующих устройств. Например, гексагональная структура графена, зафиксированная с помощью электронного микроскопа, приведена в работе [15].

В настоящей работе мы, следуя основной идее Джильберта, рассматриваем свойства фрактальных объектов, имеющих гексагональную структуру и ассоциированных с фундаментальными областями тернарных систем счисления в кольце целых чисел Эйзенштейна.

1.    Основные определения

Пусть Q ( d ) есть мнимое квадратичное поле [16]:

Q(4d) = { z = a + bid; a, b e Q}, где d < 0 - целое число, свободное от квадратов.

Определение 1. Если у элемента z = a + b4d e Q ( T d ) его норма Norm ( z ) и след Tr ( z ) есть целые числа:

Norm ( z ) = ( a + bjd )( a - b4d ) = a ² - db ² e Z ,

Tr (z) = (a + b4d) + (a - b4d) = 2 a e Z, то этот элемент называется целым алгебраическим числом поля Q( d) [17].

Сформулируем известный критерий целостности алгебраических чисел для мнимых квадратичных полей.

Утверждение. Известно [16], что при d <  0, А = | d | целыми алгебраическими числами мнимого поля Q ( i ТА) являются числа

a + bi ТА

z = ----2---- ; a , b e Z ; a = b (mod 2).

Кольцо целых элементов (целых алгебраических чисел) поля Q ( d ) будем обозначать S ( d ) , а

Z ( d ) – множество

Z (Td) = { z = a + bTd: a, b e Z} c S (Td) c Q (Td).

Таким образом, целые элементы поля Q ( i Т3) образуют кольцо:

S ( i Т3 ) = | a ⁺ bi^ , a = b ( mod2 )

называемое кольцом целых чисел Эйзенштейна.

Определение 2. Целое число Эйзенштейна а = 0,5 (B ± i43) называется основанием системы счисления в кольце

S ( i 4з )

если любой целый эле

мент этого поля однозначно представим в форме конечной суммы q (z)

z = У а,аj , a, e I. jj j=0

Если I = {0,1,...,|Norm(а)|-1} , то пара {а;I} на- зывается канонической системой счисления в кольце

S ( i4b ) [17]. Если

множество I состоит из целых чи сел Эйзенштейна, по норме меньших нормы основания а , то пара {а;I} = K называется квазиканонической системой счисления в кольце s (iVs)

. I называется ал-

фавитом системы счисления.

В работе [18] рассматриваются все возможные тернарные квазиканонические системы счисления в кольце

s ( i Vs)

и приводится следующая классифи- кацонная теорема.

Теорема. В кольце целых алгебраических чисел S(iV3) существуют ровно 24 тернарные квазиканони- ческие системы счисления, а именно: системы счисления с основаниями аk = (iV3)tok-1 и множествами цифр

{0,1, to },{0, to, to ²},{0, to ², to ³}, {0, to ³, to ⁴}, {0, to ⁴, to ⁵},{0, to ⁵, to ⁶};

где to = 0,5(1 + i V3) и k = 1,2,3,4.

Определение 3. Фундаментальной областью Ф(а, I) системы счисления {а;I} в кольце целых элементов

s ( i 4з )

поля Q (i Vs) называется множест- во всех чисел с нулевой целой частью, то есть

I V1Ф(а,I) = < У ajаj, aj e I I j=-~

Сходимость ряда (1) понимается в смысле нормы кольца целых чисел Эйзенштейна.

Определение 4. Системы счисления { а ; I } и

{ а' ; I '} в кольце S ( i43 ) будем называть эквивалентными, если существует взаимно однозначное отображение f : S ( i V3 ) ^ S ( i4*3 ) , причём f ( I ) = I' , такое, что для любого числа ye S ( i V3 ) , представи-

N мого в системе счисления {а; I} в виде у = У apаp , p=0

где a p e I , число f ( у ) в алфавите { а' ; I ' } записыва-

N ется в виде f (у) = У f (ap )(а')p . Стоит отметить, p=0

что а' не обязательно равно f ( а ) .

Модифицируя метод работы В. Джильберта, найдём размерности границ фундаментальных областей тернарных квазиканонических систем счисления в Q ( i43 ) . Для этого рассмотрим 3 случая, а именно:

• 1)    система счисления имеет основание i4"3 и множество цифр {0,1, to} . Обозначим её K1;

• 2)    система счисления имеет основание (-3 + i V3) / 2 и множество цифр {0,1, to} . Обозначим её K₂;

• 3)    все остальные тернарные квазиканонические системы счисления в кольце целых чисел Эйзенштейна.

2.    Фрактальная размерность границы фундаментальной области системы счисления K1

Рассмотрим одну из 24 тернарных систем счисления в кольце целых алгебраических чисел S ( i V3), а именно систему счисления K ₁ . Для этой системы счисления фундаментальная область Ф ₁ имеет вид, приведённый на рис. 1.

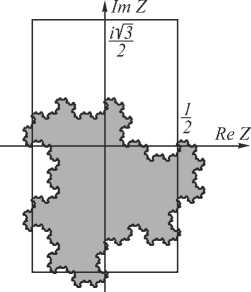
Рис. 1. Фундаментальная область системы счисления K 1

Найдём размерность границы фундаментальной области, представленной на рис. 1.

Изобразим все целые алгебраические числа z = ( a + b • i V3)/2 , где a = b ( mod 2 ) , на комплексной плоскости в гексагональной решётке (рис. 2). Из записи целых чисел Эйзенштейна ясно, что они узлы решётки, образованной из правильных треугольников, или, соответственно, из правильных шестиугольников.

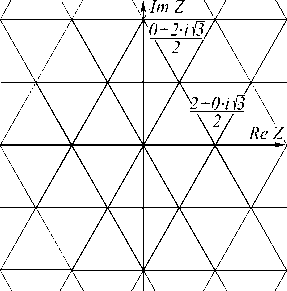
Рис. 2. Решётка целых алгебраических чисел поля Q(i 3 )

Очевидно, что для каждого узла A построенной решётки существует ровно 6 узлов A m , m = 1,. к , 6 , удалённых от него на минимальное расстояние. Пусть d_m – серединные перпендикуляры к отрезкам AA_m . Обозначим через B_m точку пересечения d m с d m _{+ 1} , кроме m = 6 , а B ₆ - точку пересечения d 1 и d ₆ . Пусть внутренность полученного правильного шестиугольника B ₁ B ₂ B ₃ B ₄ B ₅ B ₆ – окрестность точки A . Ясно, что шестиугольные окрестности двух произвольных узлов решётки не пересекаются и, кроме того, объединение замыканий таких окрестностей всех узлов решётки образует покрытие плоскости.

Для вычисления размерности границы фундаментальной области Ф 1 используем следующий рекуррентный процесс. Первоначальным приближением Ф 1 будем считать шестиугольную окрестность точки 0 со стороной 3 ^-0,5 . Каждое число с нулевой целой частью, то есть число, принадлежащее фундаментальной области системы счисления K ₁ , можно представить в ви- ~1            1 ~1                    ~1

Де X aj aj = "Т X ajа1+j , где X ajа1+j - целое ал-j=- i          а j=- i                 j=- i гебраическое число с длиной записи, не превосходящей l . Последнее равенство порождает преобразование f (p ) = -у p , определённое для всех точек p а'

плоскости. Ясно, что при таком преобразовании шес- ~ 1

тиугольная окрестность точки X aj а1+j переходит в j=- i правильную шестиугольную окрестность точки -1                                       - 1 -1

X a j а j со стороной 3 ² . 1 -приближением фунда- j =- 1

ментальной области будем считать объединение замыканий всех правильных шестиугольных окрестностей ~ 1

точек X ajаj. Такие приближения (первое и второе) j=- i приведены на рис. 3а и 3б соответственно.

~ 1

Так как количество чисел вида X aj аj равно 31, j=- i то l-приближение будет состоять из 3l правильных шестиугольников.

Таким образом, можно записать следующий алгоритм построения l -приближения фундаментальной области.

Алгоритм 1.

Шаг 1. Строим шестиугольную окрестность точки 0 со стороной 3 ^-0,5 . Полагаем v = 1.

Шаг 2. Строим все правильные шестиугольные

- 1                                         ~ V - 1

окрестности точек X ajаj со сторонами 3 2 . Если j =~ V v = I, то алгоритм закончен, иначе повторяем шаг 2 для v = v +1.

Результаты работы алгоритма (то есть последовательное приближение фундаментальной области для I = 1, 2, 3, 4, 5) приведены на рис. 3 а -3 д .

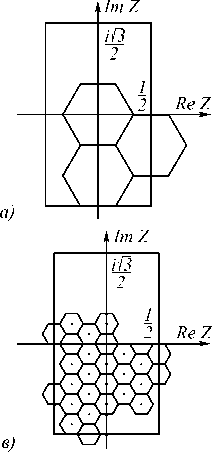
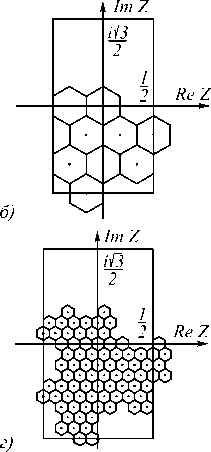
Щ 2

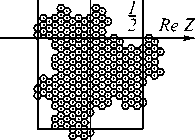
Рис. 3. Окрестности чисел с нулевой целой частью длины а) 1, б) 2, в) 3, г) 4, д) 5

Таким образом, видно, что при переходе от l -приближения к ( l +1)-приближению фундаментальной области каждому шестиугольнику l -приближения соответствует три шестиугольника ( l +1)-приближения, причём если 2 шестиугольника l -приближения имели общую сторону, то соответствующие им области в ( l +1)-приближении будут иметь две общих стороны. Поэтому количество общих сторон всех шестиугольников ( l +1)-приближения можно вычислить по формуле T _{+ 1} = 2T_i + 3^{1 + 1}, где T = 3 . Таким образом, количество сторон шестиугольников, образующих границу l -приближения, выражается по формуле L = 6 • 3¹ - 2 • T_i .

Докажем, что L_{i + 1} = 2 L_i . Действительно, 2 L_i = 12 • 3¹ - 4 • T = 18 • 3¹ - 2 • ( 2 • T, + 3 • 3¹ ) =

= 6 • 3^{1 + 1} - 2 • T + 1 = L i + 1

Отсюда следует, что L = 3 • 2^{1 + 1}.

Длина границы -приближения фундаментальной области равна произведению L на длину стороны шестиугольника, то есть

S _i = 3 • 2 ^{i + 1} • 3^{( - i - 1)/2} = 3 • ( 2/43 ) ^{i + 1}.

Получаем, что lim(Sl ) = ^ , то есть размерность границы фундаментальной области системы счисления K1 больше 1. Для определения фрактальной размерности [4] требуется, чтобы lmi Ll • (3(-1 -1)/2)d = C, 0 < C = const < +~.

Тогда размерность d границы фундаментальной области вычисляется следующим образом:

lim

1 ^^

Ll

3 d - ( 1 + 1 )

2⁽ l ^{+ 1 )}

= 3-lim—— i ^” V3 d'(1+1)

= 3 lim

1 ^^

/      у ^{1 + 1 )}

V N3 7

= const ^ — d" = 1 ^ d = log ₃ 4 = 1,26185951.

Таким образом, получаем, что 1 <  d = log ₃ 4 <  2 .

3.    Фрактальная размерность границы фундаментальной области системы счисления K2

Для данной системы счисления все рассуждения проводятся аналогично первому случаю, и в результате получается та же размерность границы фундаментальной области 1 <  d = log ₃ 4 <  2 .

4.    Фрактальные размерности для остальных тернарных квазиканонических систем счисления в кольце целых чисел Эйзенштейна

Легко показать, что фундаментальная область одной из эквивалентных систем счисления получается из фундаментальной области другой системы счисления путём применения к этой области преобразований поворота или отражения относительно оси OX . В работе [18] было доказано, что существуют ровно два вида неэквивалентных тернарных квазиканонических систем счисления. Это означает, что необходимо исследовать лишь две фундаментальные области, а именно фундаментальные области систем счисления K ₁ и K ₂ , которые и были рассмотрены в пунктах 1 и 2 данной работы.

Заключение

Предложенный подход достаточно легко обобщается как на случай других квазиканонических систем счисления в Q ( i ^ ) , так и на случай других квадратичных расширений, для элементов которых существуют алгоритмы деления с остатком по норме.

Работа выполнена при финансовой поддержке РФФИ (гранты 13-01-97007-р_поволжье_а, 12-01-00822а, 12-01-31316 мол a).