О размножении дафний в растворах экстракта биомассы спирулины, шрота косточек винограда и их композиции в соотношении 1:1 и о решении интегрально-дифференциального уравнения

Нами решались следующие задачи: 1) выявление зависимости влияния различных концентраций изучаемых веществ на процесс размножения дафний; 2) решение интегро-дифференциального уравнения, описывающего развитие плотности популяции дафний; 3) построение уравнения регрессии для плодовитости дафний в растворах водного экстракта спирулины, шрота косточек винограда и их композиции в соотношении 1:1. В экспериментах применяли стандартную методику Н.С. Строганова с использованием Daphnia magna Straus [2].

Размножение дафний в растворах экстракта биомассы спирулины, виноградного шрота и их смеси в соотношении 1:1. При рассмотрении процесса размножения дафний при различных условиях мы следовали обозначениям А.М. Наху-шева [3, 4]. Наиболее простая ситуация – нелимитированный рост численности популяции. Если предположить, что популяция равномерно распределена в области обитания ^Ω , все особи в популяции одинаковы, поколения перекрываются, то можно допустить, что средняя скорость роста популяции на одну особь (коэффициент прироста или удельная скорость)

совпадает с разностью е = r — s , где r и s - соответственно средняя рождаемость и средняя смертность. Следовательно, динамику изменения ^и ( t ) можно описать дифференциальным уравнением первого порядка:

'

U = Еи

где u - численность (плотность) популяции, t - время, ^е - мальтузианский параметр, имеющий смысл удельной скорости роста. Размерность мальтузианского параметра - время^- .

Решением уравнения (1), которое называется уравнением Мальтуса, является выражение:

и ( t ) = и (0) • e^Et

В общем случае коэффициент прироста ^е = ^{е (} u , t ), который называют также истинной скоростью увеличения численности популяции, существенно зависит и от u и от t . Экспоненциальный рост живых систем не может происходить на протяжении длительного периода времени хотя бы потому, что каждый вид, став слишком многочисленным, сам ограничивает свой собственный рост. По мере увеличения численности популяции она приближается к некоторому верхнему пределу, когда число погибших особей равно числу появившихся на свет. Кроме того, наличие дополнительных веществ изменяет этот верхний предел - уменьшает его в случае токсичности и увеличивает в случае ее отсутствия. Так, если рассматриваются процессы жизнедеятельности дафний в растворах экстракта биомассы спирулины или виноградного шрота (или их смеси), то возможно влияние этих веществ, которое зависит от их концентрации.

Обозначим S - концентрацию вещества в растворе. При больших концентрациях S смертность дафний, начиная с некоторого момента t S , начинает превышать рождаемость, и мы фактически имеем уравнение

— = r ( S ) и — q ( S ) У ( t — t_s ) и .

^dt                                   (3)

Здесь ^ ⁽ x ) =

<

1, x >  0

0, x <  0

- функция Хевисай

да. Время измеряется в сутках. Уравнение

(3) означает, что дафнии размножаются до момента t = ts, после чего начинают вымирать при q (S) > r (S) по закону и = {q(s) — r(s)}и . Дафнии начинают погибать не сразу, а начиная с момента t = ts. Это означает, что токсичные вещества на- капливаются в их организме до некоторого критического значения, несовместимого с жизнью. Так, для водного экстракта спирулины мы получаем из экспериментальной части: при S = 0,05 q(S) = 0,21, ts = 16 суток; при S = 0,025 q(s) = 0,027, ts = 16 суток; при S , не превосходящих 1,25%, q(S) = 0 - нет негативных последствий (смертность же от старости невелика). Поскольку S = 0,05 -достаточно большая концентрация, это говорит в пользу спирулины. Исходя из результатов проведённых исследований, водный экстракт спирулины является объектом средней степени токсичности для дафний (четвертый класс токсичности). Определена токсическая концентрация для дафний, она составила 5%.

Эксперимент на трех поколениях дафний также не выявил негативного влияния экстракта виноградного шрота на выживаемость и размножение дафний. Таким образом, в водном экстракте шрота косточек винограда не содержится токсичных для дафний веществ или они не растворимы в воде. Кроме того, в случае шрота величина плодовитости больше, нежели в контроле: r шрот ⁽ S ) >  r контроль ⁽ S ) .

В растворе экстракта смеси биомас -сы спирулины и шрота косточек винограда в соотношении 1:1 плодовитость ниже, а смертность выше, чем в случае спирулины той же концентрации. При s = 0,05 q(S) > 0,63, ts = 0 суток; при S = 0,01 q(S) > 0,45, ts = 0 суток; при S < 0,005 гибели дафний от экстракта не происходило.

Таким образом, в этом случае численность дафний убывает до нуля при больших концентрациях быстрее, чем для раствора спирулины, причем дафнии начинают погибать сразу. Однако гибель дафний вызвана не токсичными веществами, а гнилостными процессами в растворах.

Интегро-дифференциальное уравнение, описывающее развитие плотности популяции дафний.

Мы рассмотрели ситуацию, когда корм не ограничен. Если теперь K - поддерживающая емкость среды, то с учетом поглощения питательной среды поддерживающая емкость будет уменьшаться. Тогда скорость роста дафний будет описываться уравнением вида

'

и = ru

(

1 - и / K

I

)

- j u ( S , т ) d T

0           )

с начальным условием и (0) = и0.

Уравнение (4) - нагруженное, оно содержит интегральное слагаемое. Это не случайно. Математическое моделирование ряда процессов, изучаемых в физике, химии и биологии, нередко приводит к постановке нелокальных задач для дифференциальных уравнений - как обыкновенных, так и с частными производными [3, 4]. При t <  t s или при достаточно малых концентрациях S мы имеем следующее уравнение, к которому (4) можно свести в любом случае:

'

и = ги

-

и /

(               )

K - J u ( S, т ) d T

I     О J

и (0) = и ₀.

В решении нелинейного уравнения (6) ис-

пользуем

подстановку

t

K - J и ( S , т ) d T = z ( t ),в

результате

вида приме

нения которой получено уравнение

''              '/-<.'/ z = rz (1 + z / z)

С помощью подстановки z = p уравнение (7) сводится к уравнению вида

r p--p = r, z                                (8)

а далее к уравнению Бернулли

- q ( S Ж t - t_S ) и

z--— z = C 1 z r .

^{1 -} r                             (9)

С учётом начального условия z (0) = K получаем решение уравнения (6) в виде

и ( t ) =

и ₀ k m e - ^mt

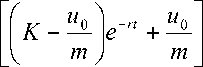
где m = ----. Решение (10) уравнения (5)

r - 1

удовлетворяет начальным условиям уравнения (5). При m >  0, r е ( -да ,0) и (1, да ) решение (10) стремится к нулю при неограниченном увеличении времени t . Это соответствует физической постановке задачи. Со временем идет поглощение питательной среды и скорость роста популяции дафний падает.

Плодовитость дафний в растворах экстракта биомассы спирулины. Мы до сих пор полагали, что r ( S , t ) = r ( S ) - не зависит от t . Но эксперимент показывает, что ситуация сложнее; выше мы рассматривали среднюю плодовитость. Построим математическую модель плодовитости дафний, следуя экспериментальным данным по их плодовитости (яйцо/самка) в ходе эксперимента. Колебания плодовитости позволяют предположить периодичность этого процесса с периодом T = 8 суток, поскольку для t = 10 суток и t = 18 су-

ток величины плодовитости практически одинаковы. Заметим также, что при увеличении концентрации спирулины плодови- тость дафний уменьшается. Учитывая характер колебаний, будем строить модель плодовитости в виде t                    ( s 1 “

r ( 5 , t ) = ( b sin n + a ) • max{1 - c — , 0}.

4                   k s о J

Здесь ⁵ о = 0,05 - предельная концентрация спирулины, при которой плодовитость дафний становится равной нулю. При

5 = 0 имеем

r0(t) = r(0,t) = b sin4n + a , рассмотрим отдельно таблицу плодовитости для 5 = 0 :

Таблица 1. Плодовитость дафний

	10	12	14	16	18	20
t X = sin — n 4	1	0	-1	0	1	0
Y = - ,( t )	3,3	4,9	7,3	5,1	3,2	6,8

Тогда зависимость Y = r 0⁽ t ) от

X = sin n

близка к линейной, поэтому целесообразно воспользоваться линейной регрессией. Линейная регрессия сводится к нахождению

S

In c + a ln— = In

S 0

k

-

-1

^r 0 J

Вновь получаем уравнение регрессии и получаем c « 1, ^a ~ ⁰,6.

уравнения вида

y x = a + b • x или y = a + b • x + s. (12)

Построение линейной регрессии сводится к оценке ее параметров – a и b . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Применяя МНК, получаем:

b = c^ov{ X , Y ^} = - 2,082, a = 5,447.

D { X }

Тогда -0 (t) = -2,082 sin 4 n + 5,447 . Най дём c и a . Из (11) имеем при 5 < 0,05:

c

( e \ “ k 5 0 J

= 1 -

r

. r ₀

Логарифмируя, имеем: