О разрешающей способности метода дирекционных магнитотеллурических зондирований

Дирекционный анализ магнитотеллурических (МТ) наблюдений [Четаев, 1985], основанный на использовании модели неоднородной плоской волны (волны Четаева), расширил возможности традиционной интерпретации при помощи модели Тихо-нова–Каньяра [Ваньян, 1997]. При этом ключевым является вопрос о разрешающей способности методов МТ-зондирований (МТЗ), или степени точности, с которой можно определить параметры (σ i , h i ) i -го слоя геоэлектрического разреза, i =1, 2, …, N , где N — число слоев в разрезе. На практике речь идет о распознавании геоэлектрических структур, вычленении зон аномальной проводимости и т. п.

Как известно [Бердичевский и др., 1986], при помощи метода МТЗ, обладающего большой глубинностью, оценивается проводимость сравнительно крупных структур земной коры. Так, в работе

[Мороз и др., 2008] оценивается разрешающая способность МТ-зондирований для определения наличия проводящих зон под Камчаткой и магматических зон под вулканами. Показано, что выделение на кривых МТЗ проводящих слоев с удельным сопротивлением ρ~10 Ом·м оказывается затруднительным, если мощность слоя h≤1.5 км. При этом достаточно тонкие слои мощностью от десятков до первых сотен метров проводящих рудных залежей или залежей углеводородов, обладающих высоким сопротивлением (ρ~1011 Ом·м), этим методом неразличимы. Использование импеданса Тихонова–Каньяра Z0, например, для мониторинга проводимости очага землетрясения также остается проблематичным в силу его малой чувствительности [Жданов, 1986]. Давая оценку сложившейся в магнитотеллурике ситуации, авторы работы [Морозова и др., 1998] приходят к выводу, что «точность методов естествен- ных полей оказывается недостаточной в свете требований, предъявляемых к изучению геоэлектриче-ского строения земной коры и вариаций электропроводности». Разумеется, речь идет о методах интерпретации МТ-полей в рамках модели однородной плоской волны, исключающей Hz- и Еz-компоненты.

Первые попытки интерпретации полного (6-компонентного) МТ-поля, выполненные для Украинского кристаллического щита способом аналитического продолжения коэффициентов отражения вниз [Четаев и др., 1984], свидетельствовали о его более высокой, по сравнению с методом МТЗ, разрешающей способности. При решении обратной задачи дирекци-онных МТЗ (ДМТЗ) методом невязки [Cавин, Израильский, 1985] было показано, что метод в принципе не имеет ограничений на разрешающую способность. Одновременно выяснилось, что малые погрешности при измерении импедансов, превышающие первые проценты, приводят к ухудшению устойчивости обратной задачи. Следовательно, при оценке чувствительности метода нельзя игнорировать степень точности полевых импедансных измерений.

Таким образом, проблема разрешающей способности ДМТЗ требует дальнейшего изучения как в применении к различным задачам геоэлектрики, так и в отношении того или иного способа решения обратной задачи.

ПОСТАНОВКА ЗАДАЧИ

В настоящей работе мы сознательно ограничимся электродинамической задачей мониторинга очага землетрясений. Предстоит выяснить, обладают ли парциальные импедансы Z ^{e, h} или коэффициенты отражения Q ^{e, h} в модели Четаева достаточной чувствительностью, чтобы надежно различать вариации проводимости очага ∆σ, составляющие, по данным работы [Поиск …, 1988], в период подготовки землетрясений порядка 10 %. Под достаточной чувствительностью будем понимать вариации ∆ Z ^{e, h} (или Q ^{e, h}) не менее 10 %, что в несколько раз превышает погрешность измерений импедансов, находящуюся в пределах нескольких процентов [Савин, Смагин, 2004]. Положительный ответ на этот вопрос мог бы служить теоретическим основанием для мониторинга вариаций электропроводности очаговой зоны, тесно связанной с динамикой напряженного состояния вещества, его физико-химическими свойствами и температурой.

Обратимся к модели внешнего МТ-поля в виде неоднородной плоской волны поверхностного типа [Четаев, 1985]. Дисперсионное уравнение для неоднородной плоской волны имеет вид

K Z = - R + i ( юцст- J ) , (1) где R = Re ( K x + K y ) , J = Im ( K 2 + K y ) , a K x и K y — горизонтальные компоненты волнового вектора K .

В критической области изменения параметров этой волны R ~ 0, стцо - J ~ 0 парциальные импе-дансы электрического Ze и магнитного Zh типа испытывают резкие изменения [Структура …, 1980]. Именно этот факт наталкивает на мысль использо- вать измерения парциальных импедансов для эффективного контроля над вариациями удельной проводимости ∆σ в очаге. Очевидно, что в данном случае речь может идти об исследовании нового электромагнитного предвестника землетрясений.

С целью теоретического обоснования указанного выше способа электромагнитного мониторинга нами выполнен математический эксперимент по изучению влияния вариаций электропроводности очага ∆σ( z ) на входные парциальные импедансы Z ^e и Z ^h слоистой среды (или коэффициенты отражения Q ^e и Q ^h).

ВЫЧИСЛЕНИЕ ПАРЦИАЛЬНЫХ ИМПЕДАНСОВ

Рассмотрим распространение волны Четаева — неоднородной плоской волны вида f, (x, y, z, t) =

= A, (z) exp(-itot + Kxx + Kyy), где Aj — любая из шести компонент электромагнитного поля в горизонтально-слоистой проводящей среде.

Амплитуды Aj(z) однозначно определяются из уравнений Максвелла rot H=σE,                                    (3)

rot E= i ωμ H                                 (4)

совместно с требованием непрерывности горизонтальных компонент поля и условием затухания при z →∞.

Для анализа комплексных амплитуд A j ( z ) оказывается удобным ввести вспомогательные скалярные потенциалы электрического U e ( z ) и магнитного U h ( z ) типов по формулам [Дмитриев, 1970]

^Ue = ^Ky^Hx - ^Kx^Hy ,                        (5)

U h = k_xh_x - K y H y .                       ⁽⁾

Компоненты электромагнитного поля выражаются через эти потенциалы следующим образом:

^H x = ( ^K x ^U h + K y U e )/ ^K 22 , H y = ( K y U h + K_xu e )/ ^K2 ,

H z = ^u h /n 2 , E x = ( K y i ^ЮЦ° ^u h ^{+ K} x П 2 ^u e )/^n ^{2 K} 2 ,

E y = ( ^K y n ^{2 U} e '^{- K} x i ®H^{C U} h )/^an ^{2 K} T2, E z =^{- iU} e /^C>

K² = K x + K y , n = V к² - i юца , Re n ^ 0.

Из (5) и (6) видно, что введение парциальных потенциалов позволяет представить электромагнитное поле в виде суперпозиции двух парциальных волн: h-типа с E z =0 и e-типа с H z =0. Кроме того, введение парциальных потенциалов упрощает систему уравнений (4), сводя ее к двум независимым обыкновенным дифференциальным уравнениям

' n2

|- e |-^ U e = 0, l-h-1- U h = 0,            (7)

^ CT J     O'           vn 7

где штрих означает производную по Z .

Уравнения (7) совместно с условием непрерывности величин U _e, U _h, U _e /ст и U _h /n 2 на границах раздела слоев (функцию σ( z ) считаем ку-83

сочно-постоянной) и условием затухания на бесконечности при z →∞ позволяют однозначно определить скалярные потенциалы и, следовательно, амплитуды волны.

Из уравнений (6) видно, что комплексные амплитуды E ^e- и H ^e-компонент волны e-типа удовлетворяют условию

E X = Z ^e H y , E y =- Z ^e H _x , (8) где Z ^e — парциальный импеданс электрического типа,

Z ^e =- U '> U _e.

Здесь Z 0 — удельный парциальный импеданс в слое с проводимостью σ, определяемый формулами (11).

Входные парциальные импедансы Z для волн e- и h-типов также могут быть единообразно выражены через парциальный потенциал U :

Z 0 U^ n U

Внутри каждого слоя проводимость σ= const , поэтому решение уравнения (16) имеет вид

U ( z ) = Ae ^{- n} z + Be ⁿ z .                           (18)

Горизонтальные компоненты волны h-типа также связаны соотношением (8), при этом величина Z ^h равна

Z ^h = i юц U '/ n ² U h .

В случае однородного проводящего полупространства (δ= const при z =0) формулы (9) и (10) приобретают простой вид:

Здесь первое слагаемое представляет амплитуду падающей волны, а второе — амплитуду отраженной волны.

Введем коэффициент отражения Q ( z ) на уровне z [Четаев и др., 1984], имеющий смысл отношения комплексной амплитуды волны, идущей вверх, к амплитуде волны, идущей вниз:

Z ^e = n/a , Z ' =— i юц/п .

Q (=)=Ae2T

В соответствии с формулами (11) выражения для действительных Re Z ^{e, h} и мнимых Im Z ^{e, h} частей импедансов обоих типов запишем так:

Используя формулу (17), получим следующее соотношение между коэффициентом отражения Q(z) и импедансами Z и Z 0 :

Re Z ^е = R + + R ² + ( юца- J ) ,              (12)

Im Z ^e

юца- J

Z = 1 - Q (z) Z0 1 + Q ( z ) ,

Re Z ^h

Im Z ^h

R + ^ R ² + ( юца J ) ²

откуда

юца- J

-JR ² - ( юца- J ) 2 -^ R + RR ² + ( юца- J) 2

yjR + Rr+ + (юца-J)

R2 +(юца-J)

Q (z ) =

1 - Z/Z 0

1 + Z ( Z 0 ) .

Поскольку входной (полный) парциальный импеданс Z зависит от глубины z непрерывно, а удельный импеданс Z ₀ претерпевает разрыв на границе раздела слоев, то и Q ( z ) является кусочно-непрерывной функцией.

Из (12)–(15) видно, что при изменении параметра J в окрестности точки J кр. =ωμσ парциальные импе-дансы претерпевают резкие изменения. Импеданс Z ^e ведет себя аналогично импедансу последовательного, а импеданс Z ^h — параллельного контура [Четаев, 1985].

Результаты многочисленных расчетов, проведенных для плоскослоистых сред [Савин и др., 1982], показывают, что и в этом случае зависимость импедансов от параметра J имеет резонансный характер, при этом

®Ц^ min ^ Jкр. ^ ЮЦатах, где σmin и σmax — минимальная и максимальная проводимости слоев.

КОЭФФИЦИЕНТЫ ОТРАЖЕНИЯ ДЛЯ ВОЛНЫ ЧЕТАЕВА

Уравнения (7), определяющие зависимость парциальных потенциалов U ^{e, h} от глубины z , удобно привести к единой форме:

I -0U' I -nZоU = 0.                         (16)In J

РАСЧЕТ КОЭФФИЦИЕНТОВ ОТРАЖЕНИЯВ ТРЕХСЛОЙНОЙ МОДЕЛИ

Рассмотрим трехслойную модель земной коры, в которой σ 3 /σ 1 =1, h 2 / h 1 =1, а удельная проводимость второго слоя, аппроксимирующего электрические свойства очага землетрясения, варьирует: (σ 2 /σ 1 ) 1 =1, (σ 2 /σ 1 ) 2 =1.1, (σ 2 /σ 1 ) 3 =0.9. Таким образом, указанным значениям удельной проводимости первого и третьего слоя соответствуют изменения проводимости второго слоя в пределах ±10 %, что отвечает реальному положению вещей в период подготовки землетрясения [Поиск …, 1988].

Возникают вопросы, могут ли указанные вариации проводимости в очаге вызвать заметные изменения коэффициентов отражения на поверхности Земли и какова относительная (в %) величина этих изменений.

Положим безразмерную толщину скин-слоя X = ^j 2ЮЦО 1 h\ = 10, а значения безразмерных величин DR = R /ωμσ 1 и DJ = J /ωμσ 1 будем варьировать в пределах от 0.5 до 1.5, что отвечает реальным вариациям параметров волны. Период вариаций положим

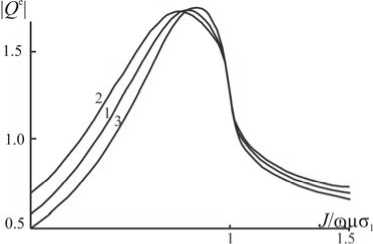
Зависимость | Q ^e | от J /ωµσ₁ при вариациях σ₂ ±10 %

T =20 c. Коэффициент отражения на поверхности Земли вычислим по формуле (21) при z =0.

Вычисления показывают, что наиболее чувствительным по отношению к изменению проводимости очага является коэффициент отражения электрической моды. График изменений | Q ^e| в зависимости от J /ωμσ 1 приведен на рисунке. Видно, что ∆| Q ^e| достигает 20 %, т. е. достаточно заметной величины, которая дает возможность эффективно исследовать проводимость очага землетрясения при помощи импедансных измерений в реальном времени.

ЗАКЛЮЧЕНИЕ

В результате математического эксперимента было показано, что разрешающая способность метода ДМТЗ позволяет проводить мониторинг очага готовящегося землетрясения в реальном времени, если вариации ∆σ очаговой зоны не менее 10 %. Выше отмечалось, что разрешающая способность МТ-зондирований зависит не только от выбора той или иной фундаментальной модели внешнего поля, но и от способа решения обратной задачи. Исследование было ориентировано на способ невязки (минимизация функционала невязки измеренных и рассчитанных импедансов [Cавин, Израильский, 1985]). Метод интерпретации ДМТЗ аналитическим продолжением коэффициентов отражения вниз [Четаев и др., 1984], претендующий на точное определение границ геоэлектрических слоев, требует специального исследования его разрешающей способности. Побочным, но тем не менее интересным практическим результатом проведенного математического моделирования явилось теоретическое обоснование возможности электромагнитного мониторинга очаговой зоны в реальном времени. Не исключено, что дальнейшие исследования помогут нащупать новый предвестник сейсмического события.