О разрешимости краевых задач для параболического уравнения второго порядка с переменным коэффициентом
Автор: Кумышев Р.М., Пантелеева М.В.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 6 (6), 2015 года.
Бесплатный доступ
Доказана однозначная разрешимость краевой задачи для одного неоднородного смешанно-параболического уравнения второго порядка с двумя перпендикулярными линиями изменения знака и коэффициента при временной производной в ограниченной области.
Cмешанно-параболическое уравнение, оператор дробного интегрирования, линия изменения типа, интегральное уравнение фредгольма, сингулярное уравнение нормального типа
Короткий адрес: https://sciup.org/140267084
IDR: 140267084
Текст научной статьи О разрешимости краевых задач для параболического уравнения второго порядка с переменным коэффициентом
Пусть область Q = {(x, t): -l < x < l, - T < t < T; l, T - const} и Lu = uxx - sign(xt^ = f (x, t). (1)
Очевидно, что (1) - смешанно-параболическое уравнение в Q с двумя перпендикулярными линиями изменения знака и коэффициента при временной производной . Нетрудно заметить, что оно будет уравнением с прямым ходом времени при xt > 0 и с обратным ходом времени при xt > 0 . Задачи подобного плана рассмотрены в работах [1]-[7].
Для уравнения (1) в области Q рассмотрим следующие задачи:
Задача 1
Требуется найти функцию u ( x , t ) со следующими свойствами:
-
1) u ( x,t ) е C ( Q ) П C 1 ( Q ) ;
-
2) u ( x , t ) - регулярное решение уравнения (1) в Q \ { x = 0 U t = 0 } ;
-
3) u ( x , t ) - удовлетворяет начальным
u (x, T) = фТ (x), u(x,-T) = ^T (x), -1 < x < 0 (2)
и граничным условиям u(-1, t) = ^ t (t), u(l, t) = ^ (t), - T < t < T, где f (x,t), фг(x), ф_TXx), у(t), ^z(t) - заданные достаточно гладкие функции, причем фт (- l ) = у -1 (T) ф-т (- l ) = у -1 (T).
Задача 2:
Требуется найти функцию u ( x , t ) со следующими свойствами:
-
1) u ( x , t ) е C ( Q ) П C 1 ( Q ) ;
-
2) u ( x , t ) - регулярное решение уравнения (1) в Q \ { x = 0 U t = 0 } ;
-
3) u ( x , t ) - удовлетворяет начальным
u ( x , T ) = афт ( x ), u ( x , - T ) = вф_т ( x ), — l < x < 0 (4)
и граничным условиям u ( - l , t ) = u ( l , t ), ux(l , t ) = 0, - T < t < T ., (5)
Более подробно изучим первую задачу.
Задача 3:
Требуется найти функцию u ( x , t ) со следующими свойствами:
-
1) u ( x , t ) g C ( Q ) П C 1 ( Q ) ;
-
2) u ( x , t ) - регулярное решение уравнения (1) в Q \ { x = 0 U t = 0 } ;
-
3) u ( x , t ) - удовлетворяет начальным
u ( x , T ) = a ( x)фт ( x ), u ( x, - T ) = в ( x)ф_T ( x ), - 1 < x < 0 (6)
и граничным условиям u ( - 1 , t ) = u ( l , t ), ux ( l , t ) = u ( l , t ), - T < t < T .,
Более подробно изучим первую задачу.
Обозначим Q + = Q П { x > 0, t > 0 } и Q + = Q П { x < 0, t < 0 } - области прямой параболичности уравнения (1), а Q - =Q П { x < 0, t > 0 } ,
Q - = Q П { x > 0, t < 0 } - области обратной параболичности уравнения (1).
Используя свойства функции u (x, t), из уравнения (1) для распределения функции u(x,0) = т(x), получаем нагруженное дифференциальное уравнение т"(x ) = f(x ,0), в силу чего и граничных условий, можно определить значение т(x). Изучая в областях Q+ и Q- для уравнения (1), соответственно задачи
u(x,0) = т(x), 0 < x < l, u(l, t) = у (t), 0 < t < T и u(x, T) = ф (x), -1 < x < 0, u(-1, t) = у t (t), 0 < t < T и переходя в полученных решениях к пределу при x ^ 0 +, соответственно, получаем соотношение, связывающее ux (0, t) и u(0, t):
"Г= J /51 (t,у/)2u^ (0П)n - J S^^uu§(0, n)dn = vn 0 (t - n) nt(n -1)1/2 '
= J K ^ ^t^ u uu ( 0 n ) d n + I (K 2 ( n v/2 u ( 0, n ) d n + f ( t ) , (8)
Vn 0(t - n) n t \n - t)
l 2
—
Где S 1 ( t , n ) = e t -n
—
l
-
1 + J e 4 ( t -n >
—
( 1 - 2 1 ) 2 1
4 ( t -n )
d l ,
к
l 2
—
S 2 ( n , t ) = 1 - e n - t
+
J
f
e
4 ( n - t )
-
( 1 + 2 1 ) 2 1 4 ( t -n )
d l ,
- 1
к
l 2
K 1 ( t , n ) = 1 ( t - n ) - e t -n
l
-
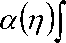
f - e 4t-n)
к
-
1 202. 1 4 ( t -n )
dl
l 2
K 2 ( n , t ) = 1 ( n - 1 ) - e n - t
+ a(n )J
f
e
4 ( n - t )
-
( 1 + 2 1 ) 2 1 4 ( t -n )
d 1 ,
- 1
к
a f (t) - функция, зависящая от заданных граничных и начальных условий задачи. После элементарных преобразований последнее уравнение окончательно принимает вид:
—
ux
(0,t)+ 1 Jf 112 ^П 0 к t 7 n -1
T 1 d n + J K ( t , n Vx ( 0, n ) d n = D 02+ F ( t ) , о
где
Г ( 1/2 )
11 1
j* z 2 ( 1 - z )- 2 "T n о dt
( z ( t - n ) + n , n ) dz +
K ( t , n ) = <
1 d
+
Г ( 1/2 ) dt
n 11 1
J z "2
n 1
n , к
^ 1
1 - z 7
dz
при n < t ,
1 d
Г ( 1/2 ) dt
да 1
J z "2
n 11
n 1
n , к
^ 1
1 - z 7
dz
при n > t .
Нетрудно показать , что индекс х уравнения (9) в классе уравнений, ограниченных при t = 0 и t = T , равен "0". Тогда это уравнение эквивалентно в смысле разрешимости уравнению Фредгольма относительно функции их ( 0, t ) . Определив из него искомую функцию, и используя след при x ^ 0 + решения и ( x , t ) в области задачи
и(x,0) = т(x), 0 < x < 1, и(1, t) = ^ (t), 0 < t < T для уравнения (1), получить для нахождения функции и (x, t)
интегральное уравнение Вольтерра второго рода. Аналогично доказывается существование и других задач.
Список литературы О разрешимости краевых задач для параболического уравнения второго порядка с переменным коэффициентом
- Сабанчиева А.А., Кумышев Р.М., Сурамова Ж.Х. О разрешимости нелокальных краевых задач для уравнения теплопроводности// В сборнике: инновационное развитие современной науки сборник статей международной научно-практической конференции. Ответственный редактор: Сукиасян А.А. 2015. С. 11-14.
- Кумышев Р.М. О разрешимости краевой задачи для нагруженного смешанно-параболического уравнения. //Российская наука в современном мире Сборник статей международной научно-практической конференции. Ответственный редактор: Соловьев В.Б. 2015. С. 197-200.
- Битова А.А., Кумышев Р.М. О нелокальной краевой задаче для нагруженного уравнения параболического типа.// В сборнике: инновационное развитие современной науки Сборник статей Международной научно-практической конференции. Ответственный редактор: Сукиасян А.А. 2015. С. 3-5.
- Кумышев Р.М. Краевая задача для уравнения смешанного типа с меняющимся направлением времени в параболической части.//Международный научно-практический журнал «Теория и практика современной науки». Выпуск № 5(5) (НОЯБРЬ, 2015).
- Кумышев Р.М. О разрешимости краевой задачи для нагруженного уравнения смешанного типа // Наука. Мысль. - 2015. - № 8; Кумышев Р.М., Маршенова Р.М., Тхашугоева О. М. Об одной краевой задаче для нагруженного уравнения третьего порядка. //ФӘн-наука. 2015. № 11 (50). С. 6-8.
- Кумышев Р.М., Пантелеева М. О разрешимости краевой задачи для уравнения третьего порядка со знакопеременным коэффициентом.//ФӘн-наука. 2015. № 11 (50). С. 6-8.
- Кумышев Р.М., Шомахова А.Ж., Ажахова Л.С. Краевая задача для нагруженного уравнения параболического типа. //ФӘн-наука. 2015. № 11 (50). С. 6-8.


