О разрешимости систем некоммутативных алгебраических уравнений, порождающих контекстно-свободные языки

Формальным языком L называют множество цепочек в алфавите { x ₁, …, x_n } выделенных с помощью конечного набора правил. Выделенные цепочки, принадлежащие свободной полугруппе { x ₁, …, x_n }^*, называются при этом либо словами (над алфавитом), либо правильно построенными предложениями (над словарем), либо грамматически правильными предложениями. Конечное множество правил, с помощью которых выделяются цепочки, называют грамматикой. Таким образом, формальный язык определяется совокупностью соответствующих правил и способом выделения цепочек с помощью этих правил.

Практически важный класс формальных языков образуют контекстно-свободные языки (кс-языки), поскольку они являются адекватным средством моделирования естественных языков, а также языков программирования [1–3]. Обозначим W = { x ₁, …, x_n } ∪ { z ₁, …, z_n } свободную полугруппу с операцией умножения; ее элементами являются произвольные цепочки, составленные из элементов «расширенного» алфавита { х ₁, …, x_n , z ₁, …, z_n }.

Рассмотрим играющее роль словаря конечное множество X = {x1, …, xn}, состоящее из слов xi языка и называемое терминальным множеством, а также Z = {z1, …, zm} – множество вспомогательных символов z,, необходимых для задания грамматических правил, называемое нетерминальным множеством; W = (Xи Z*- соответствующая свободная полугруппа относительно операции конкатенации. Дополним ее операцией формального сложения «+» мономов из множества W* (вместо суммы можно взять объединение « и », следуя работе [1]), а также коммутативной операцией умножения мономов на (целые) числа. Таким образом, можно рассматривать не только многочлены, но и формальные степенные ряды с числовыми (как правило, целыми) коэффициентами от некоммутативных переменных.

Кс-грамматика есть совокупность правил подстановки, которые каждому нетерминальному символу z, ставят в соответствие некоторый моном от терминальных и нетерминальных символов:

z ^ f 1(x, zХ-> zi ^ fq (x, z), где z 1 - особый, выделенный символ - начальный символ предложения (или программы). Правилам подстановки ставится в соответствие [3] система полиномиальных уравнений: каждому вспомогательному символу z,, содержащемуся в левой части подстановки сопоставляется уравнение z.=p, (x, z), где

Р (x ^{, z} W_t ⁽ x • z ) ^{+ +} f ^{( x} , ^z ) •

Таким образом, кс-грамматике соответствует система полиномиальных уравнений z-=p,(x, zX , = 1, -••> m,                 (1)

и кс-языком называется [3; 4] первая компонента z , решения ( z 1 ( x ), _, z m ( x )) этой системы полиномиальных уравнений, получаемого методом последовательных приближений:

z. ⁽ k ⁺¹⁾ = p_ ( x, z ^{( k} ) ), z(^ = 0, i = 1, _, m , где z ^{( k} ’ = ( z ( ^k ) ,..., z ^k ) ), 0 - нулевой моном, такой, что 0^ и = и •О = 0 для любого монома и .

В результате итераций каждая компонента z , выражается формальным степенным рядом, причем кс-язык и есть тот формальный степенной ряд, который представляет выделенный символ z 1 :

^z 1 = E <  ^z 1 , w> wC             (2)

где < z 1 , w_> - числовой коэффициент, с которым моном w от некоммутативных переменных входит в ряд z 1 . Мономы w_, являются грамматически правильными предложениями, которые могут быть построены в данном языке из слов x 1, ..., x_n этого языка, а весь ряд (2), т. е. формальная сумма всех правильных предложений, и является данным кс-языком. Построение системы уравнений (1) по грамматическим правилам языка приведено выше, причем условие того, что язык является контекстно-свободным, состоит также и в том, что многочлены p_, ( x , z ) не содержат мономов z , и e , где e - пустая цепочка. Таким образом, существование и единственность решения системы (1) обеспечивается ее специфической структурой в совокупности с методом последовательных приближений.

Рассмотрим общий случай, а именно ассоциированную с контекстно-свободными языками произвольную систему алгебраических (полиномиальных) уравнений:

q(x , z ) = 0, i = 1, ..., m .                  (3)

Решением этой системы назовем выражение символов z_i в виде формальных степенных рядов от x , подстановка которых в многочлены q . ( x , z ) обращает их в нуль. Нас интересует, каковы условия, при которых система (3) имеет такое решение, и способ получения искомых рядов.

Поставим в соответствие формальному степенному ряду (многочлену) ряд (многочлен) с комплексными переменными, задав отображение терминальных xi и нетерминальных z . символов из множества X и Z в множество комплексных переменных, причем за нетерминальными переменными zi оставляем прежние обозначения, а терминальные символы xi отображаем в комплексные переменные zi соотв етств енно, тогда (x, z) е Cm + ”. Таким образом, получаем фиксированный гомоморфизм, который ставит в соответствие формальному ряду (2) его коммутативный образ - степенной ряд от комплексных переменных ci (r) = E akz k, где k    kk akz = akv„., k„z1'... zk, ak =       E       < r, wi>,

• # x 1 ( w ) = k 1 ,...,# x „ ( w ) = k „

символ # c ( d) означает число вхождений символа c в моном d . Коммутативный образ кс-языка является алгебраической функцией, голоморфной в некоторой окрестности нуля, как показывают оценки коэффициентов степенного ряда.

Имеет место следующая теорема.

Теорема 1. Если выполнено условие

J = dC<, О,            ₍₄₎

то система (3) имеет единственное решение в виде формальных степенных рядов, выражающих вектор-функцию z через компоненты вектора x .

Для доказательства заметим, что если формальные ряды z = z(x) удовлетворяют системе уравнений q(x, z) = 0 то выполняется условие ci (q (x, ci (z (x)))) = 0.

И хотя обратное неверно, условие (4) для якобиана J обеспечивает существование и единственность решения системы ci ( q ( x, z )) = 0; обозначим это решение ci ( z ( x )). Учитывая, что условие (4) означает линейную независимость градиентов коммутативных образов многочленов, а также используя метод мономиальных меток, предложенный в [4], получаем, что это решение действительно является коммутативным образом некоторого решения исходной некоммутативной системы.

Далее, в силу невырожденности матрицы Якоби в начале координат, можно сделать линейную замену переменных z_i , в результате которой эта матрица становится единичной, что и приводит систему (3) к виду (1), в результате чего ее можно решать методом последовательных приближений. Искомые ряды равны линейной комбинации получаемых рядов.

Рассмотрим теперь системы линейных алгебраических уравнений над некоммутативным кольцом, тесно свя- занные с линейными языками [1]. Возможные методы решения этих систем в виде рядов должны учитывать как некоммутативность переменных по умножению, так и отсутствие операции деления в кольце W. Нам понадобят- ся некоторые определения.

L - операторами называются отображения L : W ^ W , действие которых заключается в умножении элемента кольца W слева и справа на некоторые мономы 1 и r : L ( z ) = 1 ■ z ■ r ■ L ( z ) = 1 • z • r

Основные свойства L -операторов:

• 1)    L(az , + P z ₂) = L(az , ) + L ф z ₂) - линейность;

• 2)    если L , ( z ) = 1 , zr , и L ₂ ( z ) = 1 ₂ zr ₂, то L , ( L ₂ ( z ) ) = L , ( 1 ₂ zr ₂) = 1 , 1 ₂ zr ₂ r , = L ₃ ( z ) - композиция L- операторов является L- оператором.

Уравнение f(z , , _, z m ) = g ( z , , _, z m ) называется приведенным, если не существует такого L -оператора R , что f ^z Р -> z m ) = Rf ^{( z} P -> z m )) и g^{( z} P -> z m ) = ^{R (} g ,⁽ z P ^’ z m ii' Если уравнение не является приведенным, то его можно привести к эквивалентному, отбросив оператор R .

Система линейных алгебраических уравнений поряд ка n над некоммутативным кольцом имеет вид

Е l ,,,, k^L,,,,k ^{( z} , ) ⁺ Е l ,,2, k^L ,,2, k ⁽ z 2 ) ⁺ ■ K ⁺ kk

+Е l,,n,kL,,n,k (zn )   Е ф,,kФ,,k, kk

Е ¹ 2,,, k^L 2,,, k ⁽ z , ) ⁺ Е ¹ 2,2, k^L 2,2, k ⁽ z 2 ) ⁺ K ⁺

k

k

‘ +E 12,n,kL2,n,k (zn ) Е ф2,kФ2,k kk

= А_. У/. ,L-.

ji I         *j , n , k j , n , k V n ) I .

V k/

При этих обозначениях и условиях имеет место следующая теорема.

Теорема 2. Порядок n системы линейных алгебраических уравнений можно понизить до - ,, если существует такая вершина r , которая смежная всем остальным вершинам n. Каждому ребру, инцидентному вершине r , соответствует одно уравнение новой системы. Очевидно, что таких ребер будет n - ,, следовательно, и порядок новой системы будет n - , (при выполнении условий теоремы для одной вершины граф инцидентности имеет вид, например такой, как на рисунке).

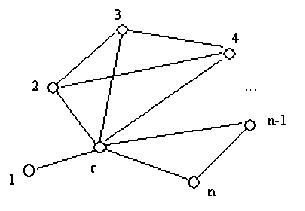
Граф инцидентности вершины r

В случае выполнения условий теоремы 2 полученная система запишется в виде

Е l n ,,, k^Ln ,,, k ⁽ z , ) ⁺ Е l n ,2, k^Ln ,2, k ⁽ z 2 ) ⁺ K ⁺ kk

+    ln,n,kLn,n,k (zn ) = Е,фn,kФn,k , kk

где l , . _k , ф i _k - действительные коэффициенты; L i . _k ( z ) - L -операторы; Ф j _k - мономы. Можно считать, что все уравнения системы являются приведенными.

Покажем, как исключать из данной системы одно неизвестное и одно уравнение. Исключаем, например, неизвестное z n . Для каждого уравнения системы оставим все слагаемые с z_n в левой части, а все остальные слагаемые перенесем в правую часть, переписав систему в виде

Е 1 ,, n , k L ,, n , k ( z n ) =

Е ^ф,, k ^ф ,, k   Е lvxk^L,,,,k ⁽ z , ) ..

kk

- Е l ,, n -,, k L ,, n -,, k ( z n -, ) , k

R

Е ^ф r , k ^Ф r , k   Е l r ,1, k^Lr ,,, k ⁽ z , )

k                 k

Е j l r , n - ,, k^Lr , n - ,, k

k

^{( z}n - , )

= ^R ,, r

^Rr ,2

Е ^ф,, k ^Ф ,, k Е l ,,,, k L ,,,, k ⁽ z , ) k                k

K    Е l ,, n - ,, k^L ,, n - ,, k

k

^{( z}n - , )

^{Е ф} r , k ^Ф r , k   ^Е l r ,,, k^Lr ,,, k ⁽ z , )

^-K ^- E l r , n - ,, k L r , n - ,, k ^{( z}n - , )

V k                                  ./

1 = ^R 2, r

Е ^ф2, k ^Ф 2, k   Е ¹ 2,,, k^L 2,,, k ⁽ z , )

kk

^- K ^- Е ¹ 2, n - ,, k^L 2, n - ,, k ^{( z}n - , ) k

,

,

2, n , k 2, n , k      n

k

= Е Ф 2, k ^ф 2, k - Е 1 2,,, k L 2,,, k ( z , ) kk

.- Е 1 2, n -,, k L 2, n -,, k ( z n -, ) , k

R

Е ^ф r , k ^Ф r , k    Е l r ,,, k^Lr ,,, k ⁽ z , )

k                 k

Е j l r , n - ,, k^Lr , n - ,, k

k

^{( z}n - , )

У 1 L A^z )=

/ J n , n , k n , n , k \ n J k

= Е ^ф n , k ^ф n , k ^- E l n ,,, k L n ,,, k ^{( z} , ^)- kk

-

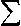
lL n, n-,, K^n, n-,, k

⁽ z n -, ) -

Е ^ф n , k ^Ф n , k   Е l n ,,, k^Ln ,,, k ⁽ z , )

k                 k

■ K Е j l n , n - ,, k^Ln , n - ,, k ⁽ z n - , )

V k                            A

Построим граф с n вершинами, i -я вершина которого соответствует Е l i,n , k L , _n , k ( z_n ) . Вершины i и j инцидентны, если существуют такие L -операторы R j и R j. , что выполняется равенство

Используя свойство линейности L -оператора, преобразуем эту систему к виду

S ^ф r , k^Rr ,1 ^(ф r , k ) S l r ,1, k^Rr ,1 ⁽ L r ,1, k ( ^Z1 ) ) kk

_

K S l r , n - 1, k R r ,1 ⁽ L r , n - 1, k k

( zn-1 )) =

= S ^ф1, k^R 1, r ^(ф 1, k ) S k\,k^R1,r ⁽ L 1,1, k ^{( z} 1 ) ) kk

_

K S l 1, n - 1, k^R 1, r ⁽ L 1, n - 1, k ⁽ z n - 1 ) ) , k

S ^ф r , k^Rr ,2 ^(ф r , k ) S l r ,1, k^Rr ,2 ^{( L}r ,1, k ⁽ z 1 ) ) k                         k

- K - S l r , n - 1, k^Rr ,2 ⁽ L r , n - 1, k ⁽ z n - 1 ) ) = k

‘ = S ^ф2, k R 2,r ^(ф 2, k ) - S ¹ 2,1, k^R 2, r ⁽ L 2,1, k ⁽ z 1 ) )

_

_

kk

■ K - S ¹ 2, n - 1, k^R 2, r ^{( L} 2, n - 1, k ⁽ z n - 1 ^ k

S Ф r , k^Rr , n ( ^Ф r , k ) - S ^lr ,1, k^Rr , n ( L r ,1, k ( Z 1 ) ) - kk

K* S\ l r , n - 1, k^Rr , n ⁽ L r , n - 1, k k

( zn-1 )) =

= S ^ф n , k^Rn , r ^(ф n , k ) S l n ,1, k^Rn , r ^{( L}n ,1, k ^{( Z} 1 ) ) kk

Так как композиция L -операторов есть L -оператор, то полученная система является системой линейных алгебраических уравнений (над некоммутативным кольцом), ее порядок равен n – 1. Тем самым порядок системы понижен на единицу, исключена неизвестная z_n .