О реакционной способности молекул во фронте сильной ударной волны

Эффекты поступательной неравновес-ности, сильно проявляющиеся в гиперзвуковых течениях многоатомных газов при формировании структур вязких фронтов сильных ударных волн, в последние годы привлекают все большее внимание исследователей, обусловленное, в частности, проблемой кластерного термояда [1].

Следует отметить, что физические причины возникновения поступательной неравновесности в вязких фронтах сильных ударных волн, могут иметь различную физическую природу. Однако ввиду совместного действия в рамках одного эксперимента, на практике они трудно разделимы и в теории часто рассматриваются как один определяющий фактор. Так, со времени основополагающей работы [2], хорошо известно, что ударная волна содержит повышенную концентрацию реакционно-способных молекул с большими (по сравнению с тепловыми) относительными скоростями. В ряде случаев эта концентрация значительно превосходит аналогичную термодинамически равновесную за фронтом ударной волны.

Второй фактор, определяющий поступательную неравновесность во фронте ударной волны, связан не столько с «неравновесной статистикой» распределения молекул, сколько с особенностями их неупругих соударений (так называемый «суперстолкновений» [1]). К числу этих особенностей следует отнести повышенные значения сечений неупругих соударений во фронте ударной волны, по сравнению с сечениями соударений за её фронтом, а также механизм стохастических соударений частиц, вызывающий так называемый резонанс Ферми [1].

Исследование поступательной неравно-весности в ударных волнах, проведённое к настоящему времени показало, что для однокомпонентного газа она должна быть незначительной. Так, в работах [3, 4] было проведено сравнение результатов вычисления функции распределения пар молекул по относительным скоростям, полученных с использованием методов Монте-Карло и Мотт-Смита. Результаты вычислений практически совпали в широком диапазоне чисел Маха набегающего потока вплоть до M 0 =10. Однако существенного влияния поступательной нерав-новесности не было обнаружено. Поэтому, с целью выявления случаев, где процессы поступательной неравновесности являются определяющими, были рассмотрены течения смесей газов с сильно различающимися величинами концентраций и масс молекул. В итоге применения как метода Монте-Карло, так и метода Мотт-Смита было получено значительное превышение количества пар высокоэнергетичных молекул внутри фронта волны по сравнению с их поступательно равновесным количеством за её фронтом [5].

Однако подобное относительное превышение, достигающее в ряде случаев значения порядка 10 ⁶ , обеспечивалось довольно искусственным заданием начальных концентраций смеси и масс молекул, выражавшемся в чрезвычайно большом различии их значений (100-кратном по составу и 10-кратном по массе). В условиях же, типичных для высокоскоростного обтекания тел, например, при спуске космических аппаратов в атмосферах планет, таких соотношений по составу смесей газов и массам их молекул, как правило, не наблюдается.

Тем не менее для таких аэродинамических условий в работе [6] эффект поступательной неравновесности был получен.

В связи с этим целесообразно провести уточнение традиционного анализа содержания пар высокоэнергетических молекул газа внутри фронта предельно сильной ударной волны при числе M g ^ то и температуре T о ^ 0.

Анализируя величину относительного превышения концентрации пар энергетически активных молекул над соответствующей концентрацией в поступательно равновесной зоне за ударной волной, полученную в работе [3], можно показать, что она имеет максимум при величине относительной скорости молекул, равной удвоенной разности среднемассовых скоростей газа перед фронтом ударной волны и за ним. Этот максимум приближённо равен величине е ² exp(1 / 2 е ), где е — величина предельного сжатия газа в ударной волне. Видно, что в одноатомном идеальном газе при е = 0 , 25 указанное относительное превышение составит величину порядка единицы. В случае структурного многоатомного газа с физико-химическими превращениями эффективное число внутренних степеней свободы будет расти, а величина параметра ε — убывать, стремясь в рассматриваемом пределе бесконечно сильной ударной волны к нулю. В силу этого максимальное превышение будет неограниченно возрастать.

Как показали численные расчёты [6], реальный физический механизм такого роста обусловлен двумя основными факторами:

• —    эффективным снижением энергетического барьера химической реакции вследствие глубокого проникновения молекул высокоскоростного пучка в область ударной волны (вплоть до р/р о ~ 1 / 2 е );

• —    немонотонным характером изменения температуры вследствие перехода части поступательной энергии молекул газа в его внутреннюю энергию.

Таким образом, в высокоскоростных газодинамических потоках указанные факторы обеспечивают эффективное протекание поступательно неравновесной химической релаксации, не требуя значительного различия молекулярных масс и концентраций компонентов смеси.

Следует отметить один класс задач с поступательной неравновесностью, когда большое разделение масс и концентраций компонентов смеси не выглядит в газодинамических условиях искусственным, а составляет существо самой задачи. Это класс задач молекулярной газовой динамики с небольшой концентрацией кластеров [7].

В работе [6] в рамках асимптотической гиперзвуковой « δ » — модели ударной волны Грэда, в её простейшем варианте — «пучок — сплошная среда», дополненной учётом химических реакций, поступательно неравновесные константы могут быть получены для любых бинарных реакций, аррениусовский вид которых известен. При этом в поступательно неравновесных константах предэкспоненциаль-ный множитель остаётся практически таким же, как и в равновесных, а экспоненциальный множитель exp( —D ) заменяется на более сложное выражение:

∞

[ Z- 1(x2 — D)n+1 /2 (e-(x-Z)2 — e-1 x+Z)2) dx, где Z и D — соответственно безразмерная скорость «пучка» относительно «сплошной среды» и безразмерный энергетический порог реакции, причём первая величина отнесена к тепловой скорости, а вторая — к тепловой энергии молекул «сплошной среды», n — показатель степени пред-экспоненциального множителя в константе аррениусовской химической реакции.

При Z = 0 выражение (1) переходит в соответствующий аррениусовский множитель в равновесной константе.

Выражение (1) даёт существенное увеличение скорости химической реакции по сравнению с законом Аррениуса, поскольку из-за большой ненулевой скорости относительного движения «пучка» и «сплошной среды» происходит как бы эффективное снижение порога реакции.

В силу структурного подобия формул, полученных для поступательно неравновесных констант, и формул для поступательно равновесных констант, первые из них будут определены при тех же значениях свободных параметров: n, D и т. д., что и вторые. Этот результат, предопределённый простотой исходной модели «пу- чок — сплошная среда», имеет существенное практическое значение, поскольку позволяет модифицировать с помощью соотношения (1) практически любые сложные системы химических кинетик, используемых в прикладных задачах.

Выражение (1) представляет интерес также и для так называемой обратной задачи: определения сечений молекулярных столкновений по известным температурным зависимостям констант скоростей химических реакций. Для поступательно равновесной кинетики такая проблема была рассмотрена ранее М.А. Рыда-левской [7]. Ввиду большой стоимости экспериментального определения сечений в поступательно-неравновесном газе, их теоретическая оценка может быть практически полезной.

В качестве теста для проверки модели и её численной реализации рассматривалась хорошо известная задача о структуре ударной волны в аргоне при числе Маха набегающего потока M ^ = 11. На рис. 1 показаны профили плотности и температуры в ударной волне, полученные в рамках модели «пучок — сплошная среда» (сплошные линии), по уравнениям Навье–Стокса (штриховые линии) и методом Монте-Карло (пунктирные линии). Все функции нормированы относительно своих значений на ±то , координата отнесена к длине свободного пробега. При этом в случае модели «пучок — сплошная среда» представлены суммарная плотность и средняя температура для смеси пучок — газ.

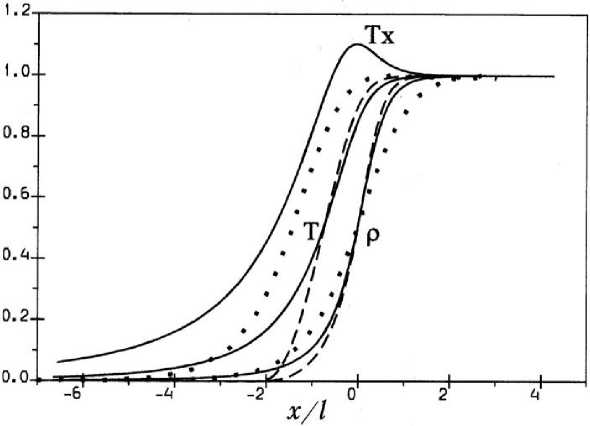
Рис. 1. Нормированные профили плотности и температуры в ударной волне

Можно видеть, что модель «пучок — сплошная среда» даёт более пологие профили, уточняя решение по сравнению с уравнениями Навье–Стокса, но все же сохраняется отличие от результатов Монте-Карло.

При наличии реакций с высокой энергией активации особый интерес представляют столкновения быстрых молекул пучка с молекулами газа. Их можно охарактеризовать эффективной продольной температурой

T x = T (1 + ( ⁽ u beam _rt u gas ) 2 - 1^ х

х

ρbeam pbeam + pgas

.

Профиль этой функции на рис. 1 имеет отчётливый максимум, превышающий значение температуры за ударной волной. Это качественно согласуется с поведением «продольной» температуры в решениях уравнения Больцмана. Повышенный уровень «продольной температуры означает, что в данной модели может быть получен эффект ускорения физико-химических процессов в ударной волне.