О реализации интерфейса передачи сообщений как облачного сервиса в агентно-ориентированных метакомпьютерных системах

Ведущие поставщики облачных сервисов – фирмы Amazon, Sun Microsystems, Microsoft, Google и другие предоставляют различные об- лачные услуги: хранение данных, в том числе в распределенных хранилищах данных, аренду виртуальных серверов, предоставление вычислительных мощностей, хранение приложений, библиотек и связанных с ними конфигурационных параметров, выбор типа операционной системы, на которой предполагается выполнять приложения, предоставление доступа к высокопроизводительным компьютерам и системам через Internet. Известны также и другие разработчики приложений как сервисов – фирмы Microsoft Dynamics, Salesforce, Taleo, Workday, NetSuite, Oracle, SucsessFactors.

С недавнего времени начали получать применение инфраструктуры и облачные сервисы, созданные упомянутыми фирмами, такие как Amazon Web Services – инфраструктура WebServices платформы в облаке и входящий в нее веб-сервис Amazon Elastic Compute Cloud, который предоставляет вычислительные мощности в облаке, Sun Cloud – сервис облачных высокопроизводительных вычислений, Windows Azure – новая серверная операционная система, предлагаемая в качестве платформы для создания облачных веб-приложений, известная ранее под названием Windows Cloud, Google App Engine – сервис хостинга сайтов и web-приложений на серверах Google.

Организация метакомпьютеров в виде облачных сервисов отражает современную тенденцию к организации распределенных вычислений, при которой используемое программное обеспечение метакомпьютера (так же, как и облачное программное обеспечение, относящееся к классу middleware) и сами обрабатываемые данные хранятся на облачных серверах, а в распоряжении клиента имеется простой Web-интерфейс.

Однако облачным технологиям присущи и некоторые недостатки, сдерживающие их промышленное и научное применение. Например, требуется постоянное соединение пользователя с Internet, трудоемко настраивание программного обеспечения, затребованного пользователем, под его собственные цели. Последние ограничения частично преодолимы путем интеграции облачных и агентно-ориентированных технологий. Например, концепция мобильных вычислений, поддерживаемая мигрирующими агентами, не требует постоянного соединения клиента с Internet.

Часть работы агент может выполнить автономно и далее передать ее результаты после того момента времени, когда клиент снова подключится к сети. Специальные агенты могут осуществлять поиск, отбор и мониторинг данных. Агенты, осуществляющие обработку данных от различных источников, могут взаимодействовать друг с другом, клонироваться и перемещаться на различные серверы. Благодаря данным функциям агентов возможно преодолеть многие недостатки и развить функциональность облачных сервисов, используя потенциально неограниченные вычислительные ресурсы и ресурсы хранения.

Благодаря агентно-ориентированным технологиям можно увеличить потенциальные возможности облачных технологий, такие как гибкая виртуализация ресурсов, высокая доступность, прозрачный доступ, простое администрирование, масштабирование вычислений и ресурсов хранения.

Метакомпьютеры как облачные сервисы

В промышленности, научных и учебных учреждениях при помощи облачных технологий можно сократить расходы на приобретение, использование и хранение программ и данных, которые могут находиться на удаленных сер- верах. Состав основных облачных сервисов, рассмотренных в работе [1] и известных также по другим работам [2-4], представлен на рис. 1. Данные сервисы выполняют в основном не вычислительные функции, а функции хранения и обработки данных. Подобно тому, как из «облака» на подключенном к сети компьютере запускаются программы, может быть организован и запуск больших масштабируемых сетевых приложений, например метакомпьютер-ных сервисов, что не нашло пока отражения в литературе.

Для метакомпьютеров обработки данных могут быть выбраны многие из показанных на рис. 1 сервисов: сервисы хранения данных (возможно, структурированных), сервисы распределенных систем управления базами данных (РСУБД), сервисы управления процессами и ресурсами, сервисы приложений и другие.

Сервисы управления процессами и ресурсами позволяют организовать единое управление многими ресурсами, например, виртуальными узлами метакомпьютера, очередями заданий, метаприложениями. Предоставляемая в качестве сервиса платформа может обеспечить разработку разнообразных метакомпьютерных приложений, в том числе распределенных баз данных.

Управление работой метакомпьютера возможно организовать с помощью сервисов администрирования и управления, позволяющих задавать параметры метакомпьютера как одного из облачных сервисов: его топологию, используемые ресурсы (данные, СУБД, вычислительные узлы и др.), уровень виртуализации и масштабирования задач. Интегрированное программное обеспечение (ПО) как сервис возможно использовать для организации интерфейсов пользователей с программным обеспечением метакомпьютеров.

Технология облачных вычислений в насто ящее время находится в стадии интенсивного развития и объединяет в своем составе многие из известных технологий, особенно технологии виртуализации. Ключевым понятием в облачных вычислениях является предоставление пользователям услуг как Internet-сервисов.

Крупные Internet-сервисы, например Amazon, Google и другие, послужили основой развития идеи облачных вычислений. Возможность увеличения объемов хранимой информации, развитие технологий виртуализации привело к созданию сетевого программного обеспечения, обеспечивающего создание вир- туальной вычислительной инфраструктуры с практически неограниченными возможно стя-ми масштабирования (при наращивании аппаратных ресурсов без значительного усложнения коммуникаций) и доступной из любой точки к Internet.

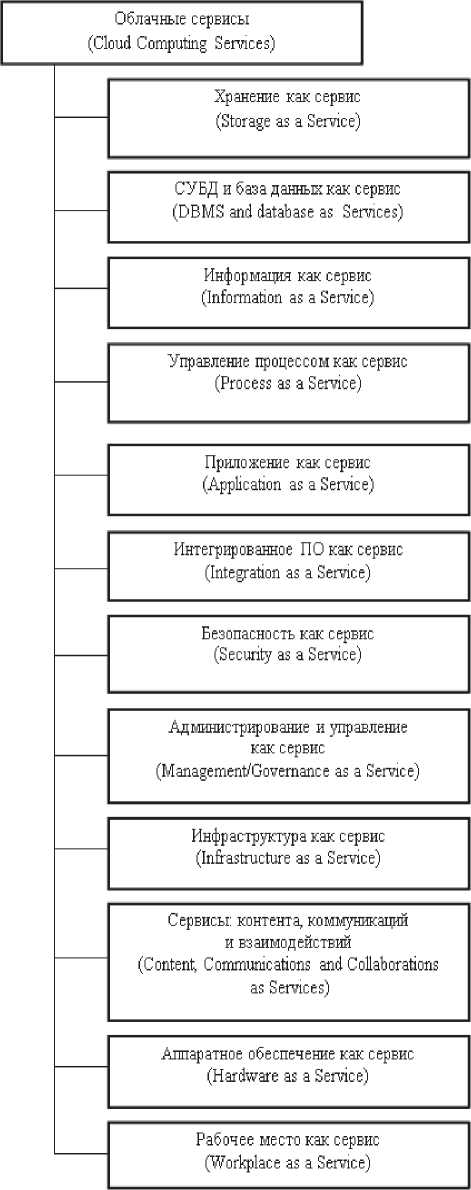
Рис. 1. Основные виды облачных сервисов

Использование предикатных сетей для формального описания интерфейса передачи сообщений

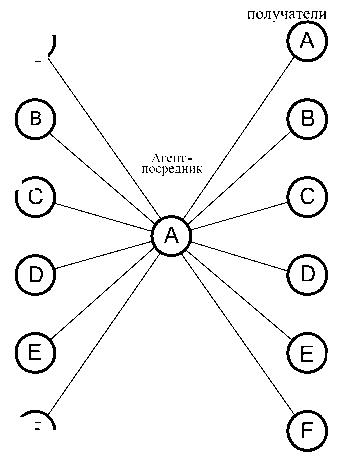
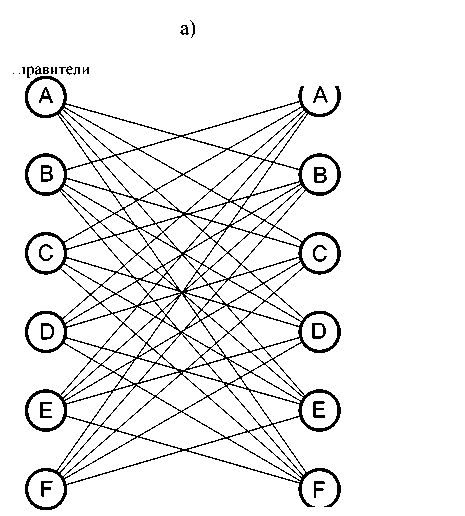
В [5-6] предложено для логического управления дискретными процессами использовать формализм асинхронных предикатных сетей (АПС). Проиллюстрировано применение асинхронных предикатных сетей для формализации основных процессов занятия и освобождения ресурсов в агентно-ориентированных метакомпьютерных системах. Далее в данной среде становится возможной организация метакомпьютерных вычислений. Следующими важными задачами являются организация управления коллективным обменом, коллективными вычислениями и синхронизация процессов. Примеры двух вариантов коллективных пересылок данных между агентами по принципу «каждый с каждым» представлены на рис. 2.

Рассмотрим четыре предикатные сети MCS_X, MCS₂, MCS₃, MCS_M реализующие при соответствующей программной интерпретации управление коллективным обменом данными и управляющими сообщениями в метакомпьютер-ных системах. Приводимые формальные спецификации относятся к классу непосредственно интерпретируемых в том смысле, что при создании распределенных программ должны учитываться только эти спецификации. Системой продукций для асинхронной предикатной сети MCS_X задается процесс логического управления в мета-компьютерной системе при передаче данных от агента A каждому из остальных агентов B , C , D , E с подтверждением приема и передачей результатов от агентов B , C , D , E агенту A .

Данная система MCS_X соответствует схеме обменов, представленной на рис. 2 а . Введены предикаты P_x, x e ^a, b, c, d, e} , характеризующие состояния процессов для мобильных агентов A , B , C , D , E соответственно. Например, если истинно высказывание №), то это означает, что агент xнаходится в состоянии X . Каждый агент x может находиться в одном из трех состояний: -^T1 (начальная фаза), ^X7 (рабочая фаза) и ^X3 (заключительная фаза). Для процесса, создаваемого агентом A , добавлено состояние <Л соответствующее широковещательной передаче сообщений каждому их остальных агентов. Этим передачам соответствуют модификации предиката P_s . Агенты B , C , D , E затем отвечают отправкой ответных сообщений агенту A , отмечая эти события модификациями предиката P_r. Затем процессы агентов переходят в рабочие состояния, завершающиеся переходами каждого из них

в заключительные состояния и модификациями предиката Pq , что сопровождает факты отправки агентами B , C , D , E сообщений об окончании работы или квитанций агенту A . Выполнение одноименных процессов A , B , C , D , E сопровождается согласованными модификациями предикатов Px , x g {a, b, c, d, e}. Инициатором начальной широковещательной рассылки сообщений является агент A . Агенты-                       Агенты- отправители                    получатели Q     ® посредник / (y /    \ ©     © a) Агенты-                         Агенты- отправители                       получатели /aY ( о      \  \          ) ©a2vzX\5XxaD 6) Рис. 2. Коллективные пересылки данных между агентами по принципу «каждый с каждым» через агента-посредника (а) и непосредственно между агентами (б) Выражения для процедур в правых частях продукций записаны в упрощенной форме. Например, выражение Pa («3 ) ^ ^P, X ) &  Pa ("1 )

в полной форме имело бы следующий вид A X) => (A X) <- ZM &^ (A X) <- hue), где &^ символ последовательной композиции операторов. Cистема продукций для асинхронной предикатной сети MCSX имеет следующий вид: MCSX: – продукции для агента A: Tax : A X) => -Pa («x ) & A («2) & A (sab) & PAsae)&PAsad)&PAsae); Ta, : A X) &  A (rbA & A (ъ ) & A Ada) & A (rea^^pa(a' W ~^Pr (rba ) & ^A (rca) &  ^A(^)&-A0;J&A(«2); Tav.pa(aJ&pq(qba)&pq(qra)&pq(qda)& pq (Че« )^pa(aJ& ^Pq (qba ) & ^Pq (qca ) &  ^Pq (4da ) ^ ~-Pq (Чеа)&Ра(Q3 )= Ta3 : A («3) ^ -^Pa (a3 WP„(axY – продукции для агента B: Ты : A (bx ) & A (sab) ^ ^Ph (bx ) & -A Aab) & Pb(b,J&P,.(raby, Tb2 : A (b. ^^Pb(b2W Pb (b3 ) & A (qba У тЬз-.рдь3^^рдьд&рдьху – продукции для агента C: TcX : A (Ci ) & A (Sae ) => -A (4 ) & -A. (Sac ) & A(c2)&AZ,); Tc2 : A (C2 ) ^ -A (c, WPc(c3W Pq {qca У, Тс3-.РДсД^^РДсД&Рс(СхУ – продукции для агента D: TdX : A (dx ) & A (Sad) ^ -A (dx ) & -A XA &  рдад&р..(г(1ау Td2 : A (d2 ^^Pd(d2W Pd (d3 ) & A (qda); Td3-.Pd(d3)^^Pd(d3)&Pd(dxy – продукции для агента E: A, : A (ex ) & A (y J ^ -A (ex ) & -A (^A & A(e2)&A(Ta); Аз: A (e. ) => -A. (e2) &  a X) &  Pq (чеа); A3:AX)^-AX)&AX). Начальное состояние сети задают следующие начальные факты (истинные атомарные константные формулы): AX), AX), AX), AX) и AX)- Имена продукционных правил,

описывающих процесс логического управления обменом данных в метакомпьютерной системе, записаны слева от ядер соответствующих продукций. Для индексации предметных констант, предикатных констант и продукционных правил здесь и далее использованы имена констант, содержащие одно- или двухбуквенные сочетания символов (например, ad , e ), либо букву и цифры (например, d 2, e 3), имеющие мнемонический смысл и заменяемые в программной реализации продукционных правил числами, выбираемыми из натурального ряда. Здесь и далее все массивы – одномерные.

Следующей системой продукций для асинхронной предикатной сети MCS₂ описывается процесс обмена данными между агентами по принципу «каждый с каждым» (через агент A ) с возвратом результатов агенту A . Данный метод управления обменом данных можно использовать также для синхронизации процессов в мета-компьютерных системах. Введены дополнительные состояния ^0 ’ ^co ’ ^o ’ ^eo для агентов B , C , D , E и не используется состояние Q для агента A . Здесь агенты B , C , D , E синхронизируют свои действия, направляя сообщения агенту A , что сопровождается соответствующими модификациями предиката P_r . Ответные посылки сообщений от агента A сопровождаются модификациями предиката P_s . Завершив согласованные действия, агенты B , C , D , E сигнализируют об этом агенту A , модифицируя предикат Pq . Начальное состояние сети задают следующие начальные факты (истинные атомарные константные формулы): ^pA^a\A РДЬД, РДсД, Р_а^ДиРДеД.

Система продукций для асинхронной предикатной сети MCS₂ имеет следующий вид:

MCS2:

– продукции для агента A :

^Pq Аса ) ^ "^a АД & P_aba ) ^&

Хз^: p„ A₃)^^РД^аз)^& p« («1);

– продукции для агента B :

T№ : Pb (b0 ^^РДЬД& Ph (b,) & Pr ДЬД;

– продукции для агента C:

P_c0 : P_c (Co) ^ -P_c (Co ) &  P_c (c,) &  p_r A_ca );

T_cX : P_c (c,) &  P_s Д_аД => -,P_C (c,) &  P_c (c₂) &

-PA^acY

– продукции для агента D:

T_d0 : P_d (d₀) ^ -^P_d (d₀) & P_d (d_x) & P_r A_day T_dx-p_d (d_x) & P_s A_ad) => ^P_dx) & P_d (d₂) &  -^Ps^adY

– продукции для агента E:

T_e0 : P_e (e₀ ^^РДеД& P_e (c.) &  P_r A_ea );

-PASacY

Те2-.РАе2)^^РДе2)&РДе3)&Р(Адет);

Следующей системой продукций для асинхронной предикатной сети MCS₃ задается процесс логического управления передачей данных от агента А по конвейеру последовательно остальным агентам B , C , D , E с возвратом результатов последовательно так же по конвейеру от агентов E , D , C , B агенту A . Введены предикаты P_x, .г e {a, b, c, d, e} , характеризующие состояния одноименных процессов для мобильных агентов A , B , C , D , E соответственно. Истинность высказывания Px Ai ) означает, что агент x находится в состоянии ^xt • Каждый процесс, реализуемый агентом x , может находиться в одном из трех состояний: X ] (начальная фаза), ^X2 (рабочая фаза) и Л"₃ (заключительная фаза). Посредством предиката P_s организуется конвейерная связь между процессами в направлении от агента A последовательно к остальным агентам B , C , D и E . Обратная конвейерная связь организована посредством предиката P_r . Такая организация удобна для реализации конвейерного обмена данными при выполнении глобальных вычислительных операций в метакомпьютерах. Начальное состояние сети задают следующие начальные факты (истинные атомарные константные формулы):

^Р_ЯА\А ^pAKb РДрУ P_d(d_x) и РДеД . Система продукционных выражений для асинхронной предикатной сети MCS₃ имеет следующий вид:

MCS3:

– продукции для агента A :

^T_a\-P_a («I) => ^„ (^ ) &  P_a Аз) & P_s Д_аД;

^Ta3 ^{: P}a Аз ) ^ -P« Аз ) ^& A. («1);

– продукции для агента B :

– продукции для агента C :

T_cX : P_s Д_ЬД & P_c (c,) ^ -,P_S Д_ЬД & ^P_c (c,) &  рдсд&-рд$_сау

^РДсД&РДсД&РД^У, Тс3;

– продукции для агента D :

Tdx^ACdWPdAA^-PsAcdW

-P_d A_XW ^pd АД& —P_s (s_de);

-,pdU2WPdU3WPArdcA

^Pd3 ^: P_d ^^d3 ) ^ ^—pd (^3 ) &  Pd Ah );

– продукции для агента E :

TeX-.PAsdeWPAex^^PAsde^& ^РДеД&РАеА;

Te2 :Pe Д2}^^РДе2)&Pe(e3) &Pr(red);

Системой продукций для асинхронной предикатной сети MCS4 задается процесс логического управления обменом данных от каждого агента каждому, причем здесь при обмене не выделяется главный агент. Данная система продукций соответствует схеме обменов, представленной на рис. 2б. Каждый агент здесь может находиться в одном из четырех состояний: x0 (фаза широковещательной рассылки сообщений от каждого из агентов всем остальным агентам), X; (фаза приема сообщений каждым из агентов от остальных агентов), •^2 (рабочая фаза) и X3 (заключительная фаза). Введены предикаты Px , x e {«, b, c, d, e}, характеризующие состояния одноименных процессов для мобильных агентов A, B, C, D, E соответственно. Система продукций для асинхронной предикатной сети MCS4 имеет следующий вид: :

– продукции для агента A :

P_a0 : P_a («0 ) &  -Pa ^ab) & -Pa A a A &

P_a (_й|) & P_a (а_аД & P_a (а₀Д & P_a (a_ad) &  Pa^aeY

Т_а2;РАаА^-РАа.А&РАаз^ ^Ta3 ^: P_a Аз ^^РДаз^ ^pa («О );

– продукции для агента B :

-.PAbbdW-PAbbe^-PbAA& pb (bx) & Pb AbA & Pb Abc) & pb (bbd) & РьАьА;

– продукции для агента C :

T_c0 : P_c (c₀) &  -.P_c (C_ca) & -,P_C (C_cb) & _P_ccdW-PACee^-PAc₀W P_c (c,) &  P_c (c_ca) & P_c (c_cb ) & P_c (C_cd ) & PACeeY

– продукции для агента D :

T_d0:P_d (Л) &  -P_d A_da) & -^P_d A_db) & ^P_dA_dc)&-P_dA_dA^-P_dAA& P_d Ax) & P_d A_dJ & P_d A_dA & P_d A_dA & PdA_dA

Pd2 : Pd Аг ) => —Pd Аг ) &Pd Аз );

– продукции для агента E :

T_e<.PAexWPA«_aA&PAM& PAc_ceWPdA_de^-PAexW PAeA&-P_uA_tA&-P_b»_be^& -^ACeeW-PdAdeY

Начальное состояние сети задают следующие начальные факты (истинные атомарные константные формулы):

. Как и остальные асинхронные предикатные сети, данная сеть функционирует, модифицируя предикаты. Каждая модификация сопровождается изменением состояния мета-компьютерной системы и может сопровождаться передачей сообщений между агентами.

О реализации интерфейса передачи сообщений в агентно-ориентированных метакомпьютерных системах

Непосредственным приложением разработанных в предыдущем разделе сетей является их использование в реализациях различного рода интерфейсов передачи сообщений, например типа спецификации MPI (Message Passing Interface).

Спецификация MPI основана на модели передачи сообщений [7-10]. Данная спецификация (обновленная версия – MPI-2) представляет значительный интерес, поскольку она стала первым стандартом систем передачи сообщений, используемых в области параллельного программиро- вания. Модель программирования MPI нередко называют моделью MPMD (Multiple Program – Multiple Data: множественный поток программ – множественный поток данных). Локальные и неструктурированные коммуникации организуются здесь с помощью двухточечных обменов, а при помощи коллективных обменов организуются глобальные операции.

Спецификация MPI, однако, не использовалась в агентно-ориентированном программировании, поскольку здесь применяются другие механизмы реализации параллельной и распределенной обработки данных. В силу того, что спецификация MPI важна для организации мета-компьютерных и облачных вычислений, целесообразно рассмотреть особенности ее асинхронной реализации для агентно-ориентированных систем. Об актуальности решения данной задачи свидетельствуют сведения о реализации интерфейса MPI поверх системы Grid в работах [11-12] на базе других технологий.

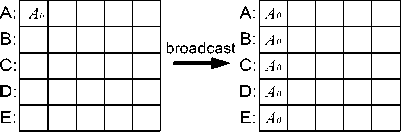
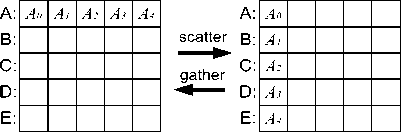
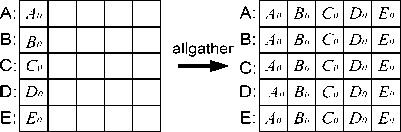
Известные схемы коллективных обменов и глобальных вычислительных операций [9] иллюстрируют рис. 3 и рис. 4 (вместо имен процессов проставлены имена агентов, реализующих данные процессы). Здесь A, B, C, D, E – имена агентов, представляющих логические узлы метакомпьютерной системы, а

A_d ? В ? S| 5 • • •, В4 ’ С_о, Cj, •••, С₄, D_o, D_x, – передаваемые данные. Рассмотренные в предыдущем подразделе спецификации логического управления глобальными вычислительными процессами в системах метакомпьютерного типа позволяют реализовать все схемы коллективных обменов и глобальных вычислительных операций, ранее примененных в интерфейсе MPI. В том числе возможно и выполнение широковещательных передач, при которых один из процессов передает данные всем процессам, обменов с барьерами, когда обмен сообщениями происходит после того, как синхронизирована работа нескольких процессов и операций приведения, при реализации которых происходит выполнение глобальных вычислительных операций.

В данном разделе с учетом предикатных спецификаций предыдущего параграфа предлагается реализовывать коллективные передачи и глобальные вычислительные операции на основе модели согласования процессов через информационное пространство, а не на основе модели передачи сообщений. Подобный подход отличается лучшей согласованностью информационной и процедурной компонент модели представления знаний, используемой непосредственно для создания управляющих программ.

Системой продукций для асинхронной предикатной сети MCS_Y задается процесс логического управления в метакомпьютерной системе при передаче данных от агента A каждому из остальных агентов B, C, D, E с подтверждением приема и передачей результатов от агентов B, C, D, E агенту A. Очевидно, что все схемы выполнения коллективных операций, представленные на рис. 3, реализуемы на базе схемы согласования процессов MCS_V Для реализации последних двух коллективных allgather и alltoall обменов необходимо последовательно инициировать работу независимых сетей MCS_{X A}, MCS_YB, MCS_YC , MCS_W, MCS_YE, в которых главными являются агенты A,B, C, D, E соответственно.

Данные

Ao	A,	Ao	Ao	Ao
Bo	Bi	Bo	Bo	Bo
Co	C,	Co	Ci	Co
Do	Di	Do	Di	Do
Eo	Ei	Eo	Ез	Eo

Ao	Bo	Co	Do	Eo
A,	Bi	c.	Di	Ei
Ao	Bo	Co	Di	Eo
Ao	Bo	Ci	Di	Ез
Ao	Bo	Co	Do	Eo

Рис. 3. Коллективные операции для группы агентов (диаграммы построены на основе функций MPI [9])

Системой продукций для асинхронной предикатной сети MCS2 описывается процесс обмена данными между агентами по принципу «каждый с каждым» (через агент A) с возвратом результатов (или квитанций) агенту A. Для реализации последних двух коллективных allgather и alltoall обменов необходимо инициировать работу одной сети MCS, .

Системой продукций для асинхронной предикатной сети MCS₃ задается процесс логического управления передачей данных от агента A по конвейеру последовательно остальным агентам B, C, D, E с возвратом результатов последовательно также по конвейеру от агентов E, D, C, B агенту A. Подобная сеть эффективно реализует логическое управление выполнением глобальных вычислительных операций, схемы выполнения которых представлены на рис. 4.

Системой продукций для асинхронной предикатной сети MCS₄ задается процесс логического управления обменом данных от каждого агента каждому, причем здесь при обмене не выделяется главный агент. Такая организация коллективного обмена данными особенно удобна при реализации операций allgather и alltoall.

Развитие аппарата асинхронных предикатных сетей – асинхронные предикатно-функциональные сети

В основу языка абстрактного описания узлов, или модулей, асинхронных предикатно-функциональных сетей (АПФС) положен язык многосортного исчисления предикатов первого порядка, расширенный правилами выборки и обновления кортежей информационного пространства, а также язык систем алгоритмических алгебр Глушкова [13 - 15]. Необходимость развития формализма сетей АПС до АПФС, например, связана с формализацией обработки данных в агентно-ориентированных метакомпьютерных системах.

При определении АПС И АПФС используется понятие блока совместимых (непротиворечивых) обновлений с последовательным выполнением правил обновлений предикатов и функций. В формальной записи блоки ограничиваются фигурными скобками. При построении сетей АПФС на основе узлов, или модулей, нами будут использоваться обычные для параллельного и распределенного программирования бинарные операции последовательного, параллельного и конкурентного выполнения модулей.

Данные

£ А: е В: < ’С: D: Е:	Л»	Во	Со	Do	Eo	А: reduce g. С: D: Е:	Ао*А1*Аз*Аз*Аз	Во-В^Вз^Вз'Вз	С<1*С1*Сз*Сз*С4	Do*D1*D2*D5*D4	Ео*Е!*Е2*Ез*Е4
	Л,	Bl	С:	Di	Ei
	Аз	Вз	Сз	D:	Ез
	Аз	Вз	Сз	Ds	Ез
	Аз	Вз	Сз	Оз	Ез

А:

В:

С:

D:

Е:

Ао	Во	Со	Do	Ео	А
А:	Bl	С.	Di	Ei	allreduce В
Аз	Вз	Сз	Оз	Ез	►с
Аз	Вз	Сз	Оз	Ез	D
Аз	Вз	Сз	Оз	Ез	Е

Ао*А1*Аз*Аз*Аз	Во*В1*Вз*Вз*Вз	С<>*С1*Сз*Сз*Сз	0о*01*02*0з*0з	Eo *E i *Ег *Ез *Ea
Ао*А1*Аз*Аз*Аз	Во*В1*В2*Вз*Вз	Со*С1*С2*Сз*С4	Do*Di*D3*D3*Do	E()*El*E2*E$*E4
Ао*А1*Аз*Аз*Аз	Во*В1*Вз*Вз*Вз	Со-ОСз-ОСз	Do *D i *D2 *Ds *Da	Eo *E i *Ег *Ез *E4
Ао*А1*Аз*Аз*Аз	Во*ВаВз*Вз*Вз	Со*С1*Сз*Сз*Сз	Do*Di*D2*D3*D4	Ео*Е1*Е2*Ез*Е4
Ао*А1*Аз*Аз*Аз	Во*ВсВ2*Вз*Вз	С»*С1*Сз*Сз*С<	Do*Di *D2 *Ds *Da	Ео*Е1*Ез*Ез*Ез

А:

В:

С:

D:

Е:

Ao	Во	Со	Do	Ео	reduce-	А:	Ао»Аг*Аз*Аз*Аз
Ai	Bl	с.	Di	Ei	scatter	В:	В(!*В!*В2*Вз*В4
Аз	Вз	Сз	Оз	Ез		С:	Со*Сг*Сз*Сз*Сз
Аз	Вз	Сз	Оз	Ез		D:	Do *D 1 *D2 *Оз *D4
Ад	Вд	С4	Da	Ед		Е:	Ео*Е1*Е2*Ез*Е4

Ao	Во	Со	Do	Ео	А:	Ао	Во	Со	Do	Eo
Ai	Bl	С!	Di	Ei	scan В:	Ао*А>	Bo*Bi	С»«С1	Do*Di	Eo*Ei
Аз	Вз	Сз	Оз	Ез	* С:	Ао^АсАз	Bo*Bi*B2	С»*С1*С2	Do*Di*D2	E()*El*E2
Аз	Вз	Сз	Оз	Ез	D:	Ао*А1*Аз*Аз	Во*ВсВз*Вз	Со*С1*Сз*Сз	Do*Di *Ог*Оз	Eo*Ei*E2*Ei
Аз	Вз	Сз	Оз	Ез	Е:	Ао*А1*Аз*Аз*Аз	Во*В1*Вз*Вз*Вз	Со*С1*С2*Сз‘Сз	Do*Di*D2*Ds*D4	Ео*ЕсЕз*Ез*Ез

Рис. 4. Глобальные вычислительные операции для группы агентов (диаграммы построены на основе функций MPI [9])

Операция « || » предписывает модулям причинно-следственную связь по крайней мере через единственный предикат либо функцию; при программной реализации применение данной операции требует дальнейшей детализации описания через операции « ; », « , » « : ».

В продукционных правилах вместо символа обновления функции или предиката «<—» может использоваться обычный символ присваивания « :=». Операция « |с» указывает на возможное конкурентное выполнение модулей, например использующих разделяемый ресурс; непосредственно при программировании данная операция не используется – ее применение требует дальнейшей детализации описания при помощи других операций, как и в случае операции « || ».

Алгебраические свойства реализуемых операций описаны в работах [16-17]. Кроме того, некоторые алгебраические свойства операций очевидны – например, операции « , » « : » ком- мутативны и ассоциативны, а операция « ; » некоммутативна и ассоциативна.

В формульной записи имена модулей, сгруппированных в блоки, заключаются в фигурные скобки, а внутри блоков могут использоваться простые скобки для указания на последовательность выполнения операций, например:

{/77,, z?z₇, /77₃}, \тп_х ,т₂}, ^т_х,т₃\т₃^, {(т_х,т₂),т₃}.

В случае когда блок содержит лишь один модуль, скобки можно опускать. В настоящей работе алгебра алгоритмов Глушкова используется в основном для записи обычных структурированных (дейкстровских) конструкций – «последовательность операторов», «ветвление», «цикл»; в принципе, здесь могла бы использоваться любая другая нотация, так же пригодная для записи структурированных программ. Все указанные выше операции мы также включаем в состав операций алгебры модулей, что облегчит формирование новых модулей сетей АПФС. Из алгебры операторов мы выбираем тернарную операцию α-дизъюнкцию и бинарную операцию α-итерацию как основы для формирования модулей АПФС (сети, при описании которых не используется операция α-итерации, в работах [18-19] принято называть сетями абстрактных машин (СеАМ), а для сетей, при описании которых используется данный оператор, выбрано название «расширенных» СеАМ, то есть РСе-АМ). Следуя [13-15], напомним правила выполнения данных операций. При выполнении операции α-дизъюнкции [а] (/И, V Z772 ) при a = tine выполняется модуль mx , а при a = false выполняется модуль m2. При реализации операции α-итерации [α]{m} модуль m выполняется циклически, пока a = false, а при a = tine происходит выход из цикла (следует отличать итерационные фигурные скобки от блочных). В сетях СеАМ и РСеАМ вместо имен модулей Ш^ > m2 и m в указанные выражения могут подставляться подформулы с символами любых из определенных выше операторов, например возможно построение следующих выражений для модулей:

m₆ = [a]({m, ,m₂,m₃} v {(m₃,m₄),m₅}), m₇ =[a,](([a₂]{[a₃](m₁ vm₂f)v {[a₄](m₃ vm₄f\

Элементарный модуль содержит единственное правило обновления предиката или функции. Пустое обновление R эквивалентно тождественному оператору E алгебры алгоритмов Глушкова, не выполняющему никаких действий по модификации информационного пространства. Неопределенное обновление R соответствует неопределенному оператору N . Продукционному программированию, применяемому в сетях АПС и АПФС, соответствует использование модулей СеАМ (модулей-продукций) следующего ограниченного вида m = [a](Z v R^e ), что эквивалентно записи m : a ^> L, где L – непустая последовательность элементарных или составных модулей. При определенных очевидных условиях данный модуль может выполняться так же, как и модуль РСеАМ, описываемый выражением MW.

Поскольку в общем случае не все составные модули непосредственно (без дополнительных преобразований или без введения дополнительных условий) допускают аналитическую запись в виде суперпозиций операций, при составлении сосредоточенных и распределенных программ рекомендуется использовать модули, допускающие аналитическое описание (то есть структурированные модули), а связи между ними организовывать посредством модификации и проверки значений функций и предикатов, составляющих информационное пространство. Такие связи называются причинно-следственными, или кау- зальными. Подобный подход позволяет использовать при распределенном программировании модули различного вида – от простых модулей-продукций до более сложных структурированных модулей.

Алгебра модулей сетей СеАМ, подобно системам алгоритмических алгебр, имеет систему образующих – элементарные модули и элементарные логические условия. Условиями называются замкнутые (не содержащие свободных вхождений предметных переменных) логические формулы с предикатными символами в качестве логических переменных. Множество используемых предикатных символов включает символы, используемые при формировании информационного пространства, а также символы стационарных, или немодифицируемых, предикатов сравнения. Используемые при сравнениях термы строятся по обычным в многоосновном исчислении предикатов первого порядка правилам (термами, или функциональными выражениями, называют слова, построенные из переменных, функциональных и специальных символов по определенным правилам). Среди элементарных логических условий важное значение имеют условия, формируемые на основе квантифицированных операторов выборки кортежей из отношений.

Определенные сети СеАМ являются в общем случае асинхронными недетерминированными системами ввиду произвольного порядка выбора на исполнение и неопределенного времени работы модулей, модифицирующих общее информационное пространство для получения полезного результата.

При проектировании систем и сетей хранения и обработки данных представляет значительный интерес построение выражений для модулей СеАМ как с использованием квант и фицированных операторов выбора 3!, 3!!, Vh V!!, так и без них. Применение квантифицированных операторов, а также дополнительных «связывающих» предикатов может привести к существенному уменьшению необходимого числа применяемых модулей СеАМ и упрощению описывающих выражений.

Учитывая, что формализмы сетей абстрактных машин мы предлагаем использовать в качестве непосредственно интерпретируемых спецификаций при создании нового программного обеспечения систем хранения и обработки данных, следует рассмотреть различные формы записи α-условий в продукционных выражениях

АПФС. При выполнении оператора 3! из области истинности предиката, описываемого выражением справа, выбирается произвольный кортеж. При выполнении оператора 3!! выбирается единственный кортеж, находящийся в области истинности стоящего справа предиката. При выполнении оператора V выбираются все кортежи, составляющие область истинности соответствующего предиката.

Оператор V!! позволяет выбрать все кортежи из области истинности предиката в случае, если его область определения совпадает с его же областью истинности. Во всех случаях подразумевается, что предикат описывается выражением, стоящим справа от символа квантифицированного оператора. Описанные операторы не удаляют выбранные кортежи из областей истинности предикатов. Модификации предикатов и функций могут быть осуществлены далее при помощи описанных выше правил обновления, сгруппированных в блоки модулей абстрактных машин.

Каждому из описанных квантифицированных операторов выборки кортежей из отношений, в случае его использования в условной части выражения для модуля, ставится в соответствие элементарное логическое условие, истинное в случае успешного выполнения оператора и ложное в противном случае. Данный факт в [18-19] отмечался подчеркиванием оператора снизу. Поскольку такой способ образования элементарного логического условия применяется только при формировании условного выражения, заключенного в полном выражении для модуля в квадратные скобки, символ подчеркивания в квадратных скобках можно опускать.

Заключение

• 1.    Рассмотрены области применения концепции агентно-ориентированного продукционно-процедурного программирования, основанного на методах логического управления вычислительными процессами и ресурсами. Решены проблемы декомпозиции, взаимодействия и синхронизации в коллективе агентов на основе согласования процессов и объектов, что позволяет усовершенствовать практические принципы построения агентно-ориентированных систем.

• 2.    Предложены модели логического управления глобальными вычислительными процессами на основе интерфейса передачи сообщений в вычислительных сетях с агентно-ориентированными облачными метакомпьютерными сервисами, основанные на коллективных пересылках дан-

• ных, что позволяет упростить реализацию массового параллелизма в крупномасштабных прикладных распределенных системах.

• 3.    Даны предложения по организации межагентных взаимодействий в сетевой среде при реализации систем управления распределенными реляционными базами данных, что повышает эффективность метакомпьютерной реализации процессов обработки структурированных данных. Кроме того, продемонстрирована возможность применения модели согласования процессов и агентов при организации обработки структурированных данных.