О реализации параллельных вычислений в системе Wolfram Mathematica

Система компьютерной алгебры Wolfram Mathematica является весьма эффективным средством вычислений. На сегодняшний день система содержит порядка 5 000 функций, многие из них написаны изначально в оптимизированном виде (особенно для низкоуровневых вычислений), а большинство операций в Wolfram Mathematica, таких как операции по снижению размерности, обработка статистических данных, обработка изображений и т.п. автоматически распараллеливаются на локальные ядра. Однако существует набор инструментов (например, ParallelSum, Parallelize, ParallelMap, ParallelTable, ParallelArray, ParallelCombine и т.д.) использование которых, при реализации многопоточных задач, призвано значительно ускорить код. Отметим, что в некоторых случаях ускорения может и не быть, или оно есть, но не достаточное по сравнению с применением других средств программирования для той же задачи. Это может быть связано с тем, что применение инструментов параллельного программирования в Wolfram Mathematica, возможно, решает задачи распределения данных и сбора результатов, не учитывая, например, накладные расходы и т.п.

Приведем несколько примеров. Все вычисления проведены на 2-х ядерном Intel Core 2 Duo с установленными лицензионными версиями Wolfram Mathematica 8.0 и Visual Studio 2010 c поддержкой OpenMP.

Проведем последовательное и параллельное вычисление суммы Е ^Д^{00 000} i реализованное на Visual Studio 2010. Результаты измерения времени вычисления приведены на рисунках 1 и 2.

Рис. 1. Последовательный алгоритм.

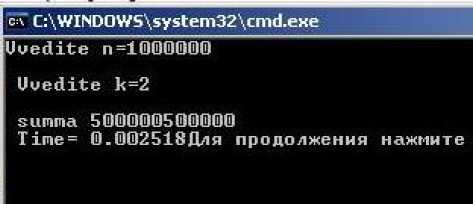
Рис. 2. Параллельный алгоритм.

Теперь произведем эти же вычисления в системе Wolfram Mathematica. Результаты приведены на рисунках 3 и 4.

ln[1l]:= Sum[i, {1, 1000 000}] //Timing)    ln[10]:= Parallels™[к, {к, 1000 000}] //Timing

Out[11]= {0.469, 500 000 500 000}              Out[1D]= {0.047, 500 000 500 000}

Рис. 3. Последовательный алгоритм.              Рис. 4. Параллельный алгоритм.

Последовательные вычисления произвели с помощью функции Sum. ParallelSum параллельная версия Sum, которая автоматически распределяет частичные сложения между различными ядрами и процессорами. Функция AbsoluteTiming возвращает реальное время вычисления своего аргумента в секундах и результат вычисления аргумента. Ее отличие от функции Timing заключается в том, что Timing измеряет количество процессорного времени, потребляемый ядром для оценки данного выражения. Ее результат лишь приблизителен, так как, в зависимости от базовой платформы, он может включать или не включать в себя процессорное время, используемое для системных вызовов, ошибок страниц и т.д. Она также не включает в себя время центрального процессора, используемого для параллельных процессов и потоков, и на ядра системы Wolfram Mathematica [3; 4].

Вычислим эффективность и ускорение алгоритмов (см. табл. 1).

Таблица 1

Эффективность и ускорение алгоритмов

Из результатов таблицы 1 видно, что E>1, т.е. мы получили суперлинейное ускорение. Это может быть связано с тем, что, например, при реализации вычислений в Visual Studio в качестве последовательного алгоритма был применен не самый оптимальный алгоритм из известных, а при вычислениях реализованных в Wolfram Mathematica увеличение количества вычислений вызвало рост суммарного объема их оперативной и кэш памяти вследствие чего, большая часть данных умещается в кэше.[1]

Рассмотрим задачу вычисления числа π. Результаты замеров времени при параллельной и последовательной реализациях в Visual Studio и Wolfram Mathematica приведены в таблице 2.

Таблица 2

Сравнительный анализ ускорения и эффективности при параллельной и последовательной реализациях алгоритма вычисления числа π в Visual Studio и Wolfram Mathematica

Из таблиц 1 и 2 видно, что время вычислений как последовательного, так и параллельного алгоритмов приведенных тестовых задач в Wolfram Mathematica существенно больше времени выполнения тех же задач в Visual Studio. Хотя ускорение, все же, достигает удовлетворительных значений и в первом, и во втором случае. Следует заметить, что при повторном запуске одних и тех же вычислений в Wolfram Mathematica получаем худший результат при параллельных вычислениях, так как система «запоминает» предыдущие действия и при запуске последовательного алгоритма не тратит время на вычисления, а при запуске параллельных вычислений тратит время на распределение данных по ядрам.

Решение этих проблем [2] при реализации параллельных алгоритмов в системе Wolfram Mathematica может состоять в выполнении следующих действий:

• 1)    при контрольных замерах времени загружать данные ядра только один раз;

• 2)    избегать необходимости обмена данными между ядрами с помощью совместно используемых данных;

• 3)    избегать повторения идентичных вычислений на отдельных ядрах.