О реализации случайных графов графами диаметров

Настоящая работа лежит на стыке комбинаторной геометрии и теории случайных графов. С точки зрения комбинаторной геометрии речь идет о некоторых аспектах проблемы Борсука для случая двумерной плоскости R ² . Назовем граф G = (V, E) (двумерным ) графом диаметров , если V ⊂ R ² , | V | <  ∞ , и

E = {{ x , y } : | x — y | = diam V := max | x — y | }. x,y ∈ V

Хорошо известно, что у любого графа диаметров хроматическое число не превосходит трех: x(G) ^ 3. Этот факт можно легко доказать по индукции (см. [1, 2]) с учетом оценки | E | ^ | V | , которая также доказывается с помощью индукции.

Рассмотрение графов диаметров напрямую связано с классической гипотезой Борсука о разбиении множеств на части меньшего диаметра (см. [3––7]). В частности, большую роль играют графы диаметров с максимальным хроматическим числом. Как мы уже говорили, на плоскости это графы с хроматическим числом 3.

В этой работе мы изучим вопрос о том, как часто встречаются на плоскости графы диаметров с хроматическим числом 3. Аналогичный вопрос для графов расстояний уже изучался в статьях [11––13].

Будем исследовать задачу в терминах модели Эрдеша––Реньи случайного графа (см. [8—10]). А именно, пусть V n = { 1,...,n } , p = p(n) G [0, 1] и G(n,p) = (fi n , F n ,P n,p ) — вероятностное пространство, в котором fi n — множество всех графов на V n без петель, кратных ребер и ориентации (так что | fi _n | = 2 C ⁿ ), F _n = 2 ^{Q n} ,

P n,p (G) = P | E | (1 - p) C ² -^{| E |} -

Иными словами, берутся случайные графы на n вершинах, в которых ребра проводятся взаимно независимо с одной и той же вероятностью p.

Настоящая работа выполнена при финансовой поддержке гранта РФФИ № 12-01-00683, гранта Президента РФ № MД-666.2012.1 и гранта НШ-2519.2012.1 поддержки ведущих научных школ.

Положим

u(n,p) = max ^ k : P _n,_p ( 3 H = (W, F) C G : | W | = k,

H = G| w , H --граф диаметров, x(H ) = 3 ) > 2}.

Таким образом, мы ищем максимальное количество вершин в индуцированном подграфе случайного графа, который одновременно реализуется графом диаметров на плоскости и имеет наибольшее возможное в этом случае хроматическое число. Если для любого k

Pn,p^3 H = (W, F) C G : |W| = k, H = G|w, H--граф диаметров, x(H) = 3) < 2, то полагаем u(n,p) = 0.

В следующем разделе мы сформулируем основные результаты для u(n,p).

• 2.    Формулировки результатов

Если функция p = p(n) вероятности ребра очень близка к нулю или к единице, то величина u(n,p) совсем мала. А именно, справедливы следующие три теоремы.

Теорема 1. Пусть p = о ^;1^. Тогда при всех достаточно больших n Е N выполнено u ( n, p ) = 0 .

Теорема 2. Пусть q := 1 — p = о ^ —1-5^. Тогда при всех достаточно больших n Е N выполнено u(n,p) = 3.

Теорема 3. Пусть q = о ^1^, но при этом qn¹'⁵ ^ то . Тогда при всех достаточно больших n Е N выполнено u(n,p) = 4.

Если и p, и q более существенно отделены от нуля, то функция u растет. В большинстве ситуаций удается найти точный порядок ее роста и даже ее асимптотику.

Теорема 4. Положим т (n) = pn и ^(n) = q ln n. Пусть t (n) и ^(n) стремятся к бесконечности с ростом n. Тогда для любого в > 0 существует такое n ₀ , что при n ^ n ₀ выполнено

u(n,p) <  (2 + в) log 1 (np).

1-p p 4 n

Теорема 5. Положим т (n) = 4-- и ^(n) = q ln n. Пусть t (n) и ^(n) стремятся к бесконечности с ростом n. Тогда для любого в > 0 существует такое n ₀ , что при n ^ n ₀ выполнено

u(n,_P) >  (² - ^в + in( -np)) ^log ,^ ( ^np ).

Поскольку в теореме 5 при больших n заведомо p > —1=, а также с учетом p ^ 1, имеем

4 n

4 in p 4 ln( np )

-

4 ln n ln( np )

> 4 —

4 ln n

³ ₄ ln n

-

Значит, во всяком случае

u(n,p) > (3 -в) log 1-p (np), и это лишь в константу раз хуже оценки из теоремы 4. Более того, если для любого а > 0

выполнено pn ^α → ∞ при n → ∞ , то ^{n p} ln( np )

^ 0, т.е. из теорем 4 и 5 мы имеем асимптотику

u(n,p) ~ 2 log 1 (np).

1- p

• 3.    Доказательства результатов

  • 3.1.    Доказательство теоремы 1

    Хорошо известно, что при p = о

    
    

• 3.2.    Доказательство теоремы 2

  n ¹ 1.5

  
  

  При q = о

  
  

• 3.3.    Доказательство теоремы 3

  Сперва покажем, что u(n,p) С 4. Поскольку q = о

  
  

  n ¹

  
  

  , то с асимптотической вероят-

  
  

n1 случайный граф является лесом (т.е. все его ком- поненты суть деревья) с асимптотической вероятностью 1. Но индуцированный подграф леса на любых к вершинах и с любым k Е {1,..., п} сам является лесом, т.е., в частности, имеет хроматическое число не больше двух. Значит, при достаточно больших n и всех k

P n,p (A(n,p, к)) =

= Pn,p(3 H = (W, F) C G : |W| = к, H = G|w, H--граф диаметров, x(H) = 3) С 2, так что u(n,p) = 0 при больших п. Теорема доказана.

с асимптотической вероятностью 1 дополнение G случайного гра- фа G до полного графа Kn является паросочетанием (набором изолированных ребер и вершин). Значит, при больших n с вероятностью больше 12 граф G содержит треуголь- ник, т.е. обладает свойством A(n,p, 3). Однако при к ^ 4 с той же вероятностью любой k-вершинный индуцированный подграф H случайного графа либо является циклом на четырех вершинах (при к = 4), либо имеет строго больше, чем к, ребер. В первом случае х(Н) = 2; во втором случае H нельзя реализовать графом диаметров на плоскости (см. введение). Значит, при к ^ 4 свойство A(n,p, к) не выполнено с нужной вероятностью.

Теорема доказана.

ностью 1 дополнение G случайного графа G до полного графа Kn является лесом. Значит, у G с большой вероятностью на любых к вершинах не более к — 1 ребер. Соответственно, у G наоборот на каждых к вершинах не менее Ck — (к — 1) = 02-1 ребер. Но из введения

мы знаем, что у любого графа диаметров на плоскости, имеющего k вершин, не более k ребер. Следовательно, свойство A (n,p, к) может иметь большую вероятность лишь при условии, что CL 1 С к, откуда к С 4.

Покажем теперь, что u(n,p) ^ 4. Для этого достаточно взять какой-нибудь подходящий граф диаметров с четырьмя вершинами, который имеет хроматическое число 3 и с большой вероятностью содержится в случайном графе. Возьмем граф A4 , представляю- щий собой треугольник, к одной вершине которого прицеплено третье ребро. На рис. 1 представлена реализация A4 в виде графа диаметров на плоскости.

Дополнением до A ₄ в полном графе служит граф, компоненты которого суть цепь P ₂ длины 2 и одна изолированная вершина. Докажем, стало быть, что при наших условиях

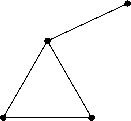
Рис. 1

случайный граф G с большой вероятностью содержит одновременно и указанную цепь, и указанную вершину.

Поскольку q = o (1), то изолированная вершина с асимптотической вероятностью 1 есть (см. [8]). На самом деле здесь хватило бы даже условия q = c l”ⁿ с любым c <  1.

Пусть теперь X –– случайная величина, равная количеству индуцированных копий P 2 в случайном графе G. Нам достаточно установить асимптотику P n,_q (X ^ 1) ^ 1, n ^ то . Применим неравенство Чебышева:

DX

( MX ) ² '

P _n,_q (X >  1) = 1 - P _n,_q (X <  0) = 1 - P _n,_q (MX - X >  MX ) >  1 -

Обозначим через M f X второй факториальный момент величины X. Тогда DX = M f X + + MX - (MX ) 2 , т.е.

• -DX, = i- f,-   +

¹    ( MX ) ^{2   1}    ( MX ) ²    MX ⁺ 1'

Если мы проверим, что MX ^ то и M^X ~ (MX ) ² , то правая часть последнего равенства будет асимптотически равна единице и теорема будет доказана.

Во-первых, MX = 3C n3 q 2 p. Далее, MX = Ө (n ³ q ² ), поскольку p ^ 1. Но по условию теоремы qn ^1.5 → ∞ , и, стало быть, n ³ q ² → ∞ . Первая асимптотика проверена.

Во-вторых,

M^X = £ MX h i ,h 2 ,

H 1 ,H 2

где суммирование ведется по всем упорядоченным парам различных графов H 1 , H 2 ⊂ K n , изоморфных графу P 2 , а X H ₁ ,H ₂ –– индикатор одновременного попадания графов H 1 , H 2 в случайный граф G в качестве индуцированных подграфов. Если выделить те слагаемые, в которых графы H ₁ , H ₂ имеют непересекающиеся множества вершин, то получится величина 9С П С П_{- 3}^ ² р) ² ~ (MX ) ² . Нетрудно видеть, учитывая асимптотику qn ¹'⁵ ^ то , что остальные слагаемые бесконечно малы по сравнению с указанной величиной. Таким образом, мы действительно имеем M ² X ~ (MX ) ² .

Теорема доказана.

• 3.4.    Доказательство теоремы 4

Сперва докажем вспомогательную лемму.

Лемма 1. Пусть в графе G , имеющем n вершин, для некоторого k < n выполнено следующее условие: у любого индуцированного подграфа H графа G , имеющего k вершин, число ребер строго больше k . Тогда для любого l > k выполнено то же самое, т.е. у любого индуцированного подграфа H графа G , имеющего l вершин, число ребер строго больше l .

Доказательство леммы 1. Достаточно доказать утверждение леммы при l = к + 1. Пусть G = ({1,..., n},E). Пусть также W = {w1,..., wk+1} С V. Рассмотрим W ‘ = = {w1,...,wk}. По условию леммы |E(G|w‘)| > к. Если |E(G|w‘)| ^ к + 2 = l + 1, то тем более |E(G|w)| ^ l + 1, и нужный факт установлен. Предположим, стало быть, что |E(G|w‘)| = к + 1. Если теперь хотя бы одно ребро идет из wk+1 в W‘, то снова |E(G|w)| ^ к + 2 = l + 1, и все в порядке. Допустим, однако, что из Wk+1 ни одно ребро не идет в W‘. Поскольку |E(G|w‘)| = к + 1, в W‘ есть хотя бы одна вершина графа G|w‘ степени не меньше двух. Без ограничения общности это w1. Рассмотрим W‘‘ = {w2,..., wk+1}. С одной стороны, сделанное выше допущение означает, что |E(G|w‘‘)| С |E(G|w‘)|-2 = к — 1. С другой стороны, |W‘‘| = к, так что по условию леммы |E(G|w‘‘)| ^ к + 1. Противоречие, и лемма доказана.

Зафиксируем е > 0 (см. условие теоремы 4) и положим к = k(n) =

(2 + е ) log _i_ (np)

1- p

Прежде всего покажем, что к ^ то . В самом деле, с учетом неравенства — ln(1 — p) <

p

имеем

1— p

log i (np) = 1- p

ln( np )

— ln(1 — p )

(1 — p ) ln( np )

p

Значит, если p ^ 1, то, поскольку np ^ то , получаем к ^ то . Если же p ^ 1, то заменяем 1 — p = q на i ^ (см. условие теоремы) и получаем, в свою очередь,

(1 — p ) ln( np )     a ( n ) ln( np )

----------- = ---:----- ~ ^(n) ^ ТО p              p ln n         v 7

Далее, снова воспользуемся тем фактом, что у любого графа диаметров на плоскости, имеющего k вершин, число ребер не больше k .

Обозначим через A _k событие, состоящее в том, что у любого индуцированного подграфа H случайного графа G , имеющего k вершин, число ребер строго больше k . Положим P k = P n,p (A). Если найдется такое n g = n g ( е ), что при всех n ^ n g выполнено P k > 2 ,то с вероятностью, большей половины, в случайном графе G не найдется индуцированного подграфа H , представимого как граф диаметров и имеющего k вершин. А по лемме 1 не найдется и такого подграфа большего размера, т.е. u(n,p) < к.

В дальнейшем мы покажем, что P k ^ 1 при n ^ то , и это завершит доказательство теоремы 4.

Обозначим через X _k случайную величину, равную количеству индуцированных k -вершинных подграфов случайного графа, имеющих не более к ребер. Тогда P k = P _n,_p (X _k = 0) и с учетом неравенства Маркова

P k = P n,p (X k = 0) = 1 — P n,p (X k >  1) >  1 — MX k , так что остается доказать асимптотику MX k ^ 0. За счет линейности математического ожидания получаем

k

MX k = C k үе_с 22 p q C -.

i=g

Убедимся в том, что в этой сумме максимальным является последнее слагаемое. Для этого разделим (i + 1)-е слагаемое на i-е (0 С i С к — 1) и проверим, что отношение не меньше единицы:

i⁺¹ r>i⁺¹ a ^C 2 ^— i- ¹

C C 2 ^{p q} = C 2 ^— i • p

С^г_С 2 p'iqC k - i         i + ^{1 q}

Понятно, что функция

Ck2 - i i + 1

убывает по i. Значит,

C k ^— i • p >  C k ^— k ⁺¹ • p >  C k ^— k • p = k — 3 • p i +1 ' q ^/ k " q ^> k " q ^— 2 " q '

Мы хотим показать, что

k — 3 p -i — • q > ¹

а покажем даже, что

k — 3

· ^p → ∞ . ^q

Упростим, стало быть, запись

и рассмотрим выражение

— ln(1 — p) <  i p p , имеем

kp

.

q

Поскольку np → ∞ и

kp     2ln( np )

^q — — ln(1 — p )

1 — p > 2ln(np) ^ to.

Итак, при больших n

MX _k <  (k + 1)С П C C 2 p k q C k - k . k

Воспользуемся простыми оценками C a ^

( 3 a ) и C a <  Oy . Получаем

MX k <  (k + 1) ( 3 n ) k      p k q C k - k <  ( 3 n ) ‘ k 2k p k q^C k - - <  ( 3 n ) ‘ k i kk pp k q^c k - =

\ ГҮ / rv.                       \ rv / rv.                     \ rv /    ( k/e )

k ( k -3)                   k -3 ^k

= (3e) k n k p q ²    = (3enpq ² I .

Теперь для завершения доказательства теоремы достаточно проверить, что в ее усло- k-3

виях величина npq 2 стремится к нулю. Итак, k-3

npq ² < exp

((1 + 2)

ln( np ) ln q

In q + ln(np)^ = exp ( — | ln(np) )

^ 0.

Теорема доказана.

• 3.5.    Доказательство теоремы 5

Зафиксируем e > 0 и положим k =   2 — e + -^n-plog(np)l .

ln( np ))      1 - P     J

При доказательстве теоремы 4 мы уже, по сути, убедились в том, что k → ∞ : в самом деле из раздела 2 мы знаем, что

^ 2 — e +

4lnp                 /2

ІПЫ ) log p(np) > (3 — e) log p(np)- а неограниченный рост последней величины мы установили при доказательстве теоремы 4 даже в более слабых ограничениях на функцию p.

Нам достаточно показать, что при больших n выполнено u(n,p) >  k. Наличие целой части не играет никакой роли, т.к. k → ∞ и при необходимости мы просто можем заменить

Е на е' Е (0, е). В дальнейшем некоторые неравенства будут выполнены лишь при n ^ П о , но мы не будем каждый раз говорить об этом.

Любой цикл с нечетным числом вершин можно реализовать на плоскости как граф диаметров с хроматическим числом 3. Обозначим через Y k случайную величину, равную количеству индуцированных k-вершинных подграфов случайного графа G, являющихся циклами. Если мы докажем, что при больших n выполнено P _n,p (Y k > 0) >  2 , то при тех же n мы получим u(n,p) ^ к. Как всегда, мы докажем еще больше: P _n,_p (Y k > 0) ^ 1.

В силу неравенства Чебышева (ср. § 3.3) имеем

P n,p (Y k > 0) = P „,p (Y k >  1) >  1 - ——2.

Как и в параграфе 3.3, остается установить две асимптотики: MY _k ^ то и M f Y _k ~ (MY _k ) ² . За счет линейности математического ожидания имеем

MY k = С П (k-Д p k q C^- .

Нетрудно видеть, что к = Ө flog i (np)) < Ө f ^nn—< Ө flnn) = Ө f ^nrrn) = o № • \ 6 ~           ^-ln(1 - p) у V p /     \r(n)lnn)         7

k

Поэтому C n ~ k^ и

MY, _ n k ^{(k - 1)!} ^aCl-k ₌ nk^QCl-k > ±ті^кт)^ка²2‘² = -1- U •по²)²'^

MY k k !   2 ^pq 2 k pq >  2 k npq 2 k W ⁷ •

Поскольку к ^ то, для обоснования асимптотики MYk ^ то достаточно найти такое 5 > 0, что npqk)2 = exp fln(np) + 2 ln q) > 1 + 5.

Это равносильно существованию такого 5 > 0, что ln(np) + k ln q ^ 5. После подстановки явного выражения для k имеем ln(np) + (2 - Е' + 4ln p ^ ^n(np!

ln q =

² 2 ^£ ) ln(np) - 2 ln p = I ,- ln(np) - 2 ln p > ^2 ln(np) ^ то ,

\        ln( np ) у -2ln q

= f1 - и все доказано.

Проверим теперь асимптотику M²Y _k ~ (MY _k ) ² . Как обычно,

M ^ Y k = 52 MY C 1 ,C ₂ ,

C 1 ,C 2

где суммирование ведется по всем упорядоченным парам различных k -вершинных циклов С 1 ,С ₂ С K n , а Y c 1 ,c ₂ —индикатор одновременного попадания циклов С 1 ,С ₂ в случайный граф G в качестве индуцированных подграфов. Как и в параграфе 3.3, отдельно рассмотрим слагаемые с V(С 1 ) П V(С ₂ ) = 0 и слагаемые с V(С 1 ) П V(С ₂ ) = 0. В первом случае получаем выражение

Q k^k ( ^{( k 1)!} „k C 2 - k А      (k ( k ^{( k 1)!} „,k C2-k A      / 2,TV Y

S i = C n C n - k I —2— pq ^k ) ~ \^C n —2— pq ^k ) = ^{( MY} k ) •

Предпоследний переход сделан за счет k = o ( 4/n). Если покажем теперь, что

S 2 = Е Y^-C'- - S 1 = °((M ^yk ) ² )>

C 1 ,C 2

то завершим доказательство теоремы.

Для каждой пары циклов Ci, C2, которые различны, но пересекаются хотя бы по одной вершине (именно такие пары задают S2) можно найти число общих вершин (обозначим его через m = m(c1,c2)) и число общих ребер (обозначим его через l = l(c1,c2)). Очевидно, что m G {1,..., k — 1}, l G {0,..., m — 1}. Таким образом, k—1 m—1

S 2 < E E c n c n — m

m=1 l=0

c m f У p ^2k—l q ²(C k ^—k>^—C m +

Допустим, мы доказали, что при всех m, l

_c k_c^k—m_Cm ( (k _ 1)! V ² 2k — l 2(C 2 — k) — c m +l

C n C n — k Ck у 2 J ^p q

C n c n - k (k . . ¹ Г' P ^2k qq      ^k)

= o Ш-

Тогда

S ₂ <  k ² C n C n — k ( ' k 2 ' ^, ’ ) ² p ^2k q-        • o (i) =

= o fc n c n — k f ( k 2''' ) ² p ^2k q k )

= o((MY k ) ² ),

и теорема доказана. Итак, имеем

c^k0^k—m0^m ( (k_j V ^{2k —} l ²⁽C 2 ^—k^)— C m ⁺l

C n C n — k C k у 2 у ^p q

C k cLk ( Т ) ² p ^2k q ^{2(c 2 — k)}

k ⁽ k - 1) • . . . • ( ^{k —} m + 1)    c m _p- l _q — C' m +l _<

( n — 2 k + 1) • ... • (n — 2 k + m ) ^k

< 2k ^2m n ^—m p ^—l q ^—C m ^+l < 2k ^2m n ^—m p- m⁺¹ q- C m

Остается показать, что при всех m G { 1, ..., k - 1 } выполнено

k^k^ m n ^m p ^m+1 q C m = _ex p ^ (2m + 2) In k — m In n — (m — 1) In p — c m In q ) ^ 0.

Если рассмотреть выражение в показателе экспоненты как функцию от m, то ввиду неравенства In q <  0 это квадратичная функция с положительным коэффициентом при m ² . Значит, ее максимум по m достигается либо при m = 1, либо при m = k — 1. При m = 1 имеем (с учетом k = o (^n))

4ln k — In n = In knn^) = ln(o(1))

→ -∞ ,

и все доказано. При m = к — 1 имеем

2k ln к — (к — 1) ln n — (k — 2) In p — C 2 - 1 In q <  к ^ln(k 2 ) — k — 2 ln(np) — = к ( 2 ln( np )+ (k = к ln(np) ^ 2 2 £

< к ^ln(k 2 ) — k k 2 ln(np) — 2 ln q^ < f     , 4ln p \ ln( np )    \ (   6 + ln( np )J —2ln q lnq) = 1^ ln(np) + ln(k 2 ) + 2 lnp^ = — 1 , 2 , ln( kp ) 2 A = k    ln( np ) у =         f- ^‘ + 2 + ln( kp ) 2 A к ln( np )     2 + k + ln( np ) J •

Ясно, что 2 ^ 0. Более того, k ln(kp)2 < ln (6-in(i-p)p) < ln (36ln2(np))    ln 36 + 2 ln ln(np)

ln( np )          ln( np )              ln( np )               ln( np )

В итоге

к ln(np) —- =' + 2 + inM) < — n p ^, у 2 k ln(np) у4

и снова все в порядке.

Теорема доказана.