О решении краевых задач теории упругости методом ортогональных проекций

Метод ортогональных проекций имеет большое значение для решения различных задач математической физики, т.к. позволяет найти обобщенные решения для широкого класса областей [1]. Эффективное применение этого метода в теории упругости стало возможным после введения энергетических гильбертовых пространств тензоров напряжений [1]. В данной работе приведено систематическое изложение результатов, полученных автором в течение ряда лет по проблеме применения метода ортопроекций, основанного на теории энергетических пространств, для решения краевых задач теории упругости при заданных объемных и поверхностных силах [2-7].

Пространства L ₂, L^v ₂, L^t ₂

Пусть V – область в трехмерном евклидовом пространстве R ³ , ограниченная кусочно-гладкой поверхностью Г. Множество вещественных функций, определенных почти везде в V и квадратично суммируемых в V , есть линеал. Определим на этом линеале скалярное произведение, полагая [8]

( ф , у ) = J ф ( x ) у ( x ) dV ,

V где x – переменная точка области V . Введя скалярное произведение, этот линеал превращен в вещественное сепарабельное гильбертово пространство L2 (V) с нормой

II ф| |2 = ⁽Ф , Ф ) .

Возьмем теперь линеал векторных функций, каждая из которых имеет компоненты, принадлежащие к классу L ₂ ( V ) . На данном линеале введем скалярное произведение по формуле

( u , v ) = J u • v dV ,

V где u,v – трехмерные векторы, а точка обозначает обычное скалярное произведение векторов. Тем самым получаем гильбертово пространство Lv2(V) с нормой ||u||2 = (u,u), обладающее свойствами пространства L2 (V) .

И, наконец, рассмотрим линеал симметричных тензоров второго ранга с компонентами, принадлежащими классу L ₂ ( V ) . Превратим его в гильбертово пространство, определив на нем скалярное произведение и норму по формулам [9]

^| p,q ^] = J p q dv , Ц |2 = [ p,p ^] ,

V где двумя точками обозначено двойное скалярное произведение тензоров [10]. Данное пространство Lt2 (V ) также обладает всеми свойствами пространства L2 (V ) .

Энергетические пространства тензоров второго ранга

Возьмем симметричный положительно определенный тензор четвертого ранга S(x), x g V, в общем случае неоднородный и анизотропный. Будем рассматривать его как положительно определенный оператор, действующий в полном гильбертовом пространстве L2 (V) по правилу S --p = q, p,q g L2 (V). Построим энергетическое пространство T(V) [1], определив на элементах из Lt2 (V) скалярное произведение и норму по формулам

( q , p ) = ^[ q , S -- p ^] = J q -- S -- p dV , |p| |2 = ⁽ p , p ).                         (1)

V

Непосредственно проверяется, что данные выражения удовлетворяют всем аксиомам скалярного произведения и нормы [1]. А именно ( X 1 q 1 + X 2 q 2 , p ) = X 1 ( q 1 , p ) +X 2 ( q 2 , p ) ( X 1 , X 2 - const, p , q 1 , q 2 g T ) ; далее в силу положительной        определенности тензора          S          имеем

( p , p ) = J p -- S - - p dV - X J p - - p dV - 0 ( X >  0 ) и, если ( p , p ) = 0, то p = 0; наконец, VV

( p , q ) = J S _аву5 q _a₽ p _y5 dV = ( q , p ) (суммирование по греческим индексам а , в , у , 5 = 1,2,3). V

Пространство T (V ) из-за положительной определенности оператора S и сепарабельности исходного пространства Lt2 (V)  обладает всеми свойствами пространства Lt2(V) [1].

Выделим в пространстве T ( V ) подпространства

T = { p ' : e '= S p ' , e '= def u } , T 2 = { p" : V- p" = 0, n - p" = 0 } , замкнутые своими предельными точками. Здесь п – вектор внешней нормали к поверхности Г, и - вектор с компонентами из L ₂ (V ), V - дифференциальный набла-оператор ( V - p" = div p '' ) [10], def- оператор деформации, преобразующий вектора из

L^v ₂ ( V ) в симметричные тензоры второго ранга, компоненты которого определяются по правилу e ' j = ( def u ) ,,■ = 0-5 ( « , . jj + U ji ) , где u i - координаты вектора, запятой обозначается производная по соответствующей координате x_i точки области V ( i , j = 1,2,3 ) .

Элементы подпространства T ₁ можно трактовать как тензоры напряжений, являющиеся решениями краевой задачи теории упругости

• V- p ' = f , e ' def u , p '= C -- e ' , n - p ' = t (2) при всевозможных объемных и поверхностных силах. Здесь f ( x )( x g V ) - вектор объемных сил, t ( x )( x gF ) - вектор поверхностных сил, C = S ^{- 1} - тензор модулей упругости, S - тензор модулей податливости, p ' - тензор напряжений, e ' - тензор

деформаций, V- p '= f - уравнения равновесия, n - p '= t - граничные условия в напряжениях. Элементы подпространства Т ₂ можно трактовать как решения краевой задачи

• V- p '' = 0, e ' = def u , p '' = C -- (e '- e * ) , n • p ''= 0 (3) для всевозможных симметричных тензоров второго ранга е * . Тензоры p '' представляют собой тензоры собственных самоуравновешенных в области V напряжений, возникающих в теле при создании в нем поля первоначальных (собственных) деформаций, заданного тензором е * . При данной трактовке норма (1) задает выражение для потенциальной энергии упругих деформаций.

Пространство Т является ортогональной суммой подпространства Т ₁ и T ₂ , то есть Т = Т 1 ® Т 2 . Действительно, если p 'е T 1 , а p ''е T ₂, то, используя формулу Остроградского – Гаусса, находим

( p" , p ) = J p ''-- S -- p ' dV = J p ''-- e ' dV = J p ''-- def u dV = - J v - p ''• u dV + J n - p ''• u d r = 0. V V V V г

Отсюда подпространства Т 1 и T ₂ ортогональны. Далее любой тензор p е T всегда можно единственным образом представить в виде p = p ' + p '' ( p ' е T 1 , p '' е T ₂ ) . Предположим, что составляющие тензора р непрерывны и непрерывно дифференцируемы в ( V + г ) . Найдем V- p = f ' , n - p = t ' и из решения задачи (2) с данными значениями объемных и поверхностных сил определим p ' е T 1 . Теперь достаточно положить p ''= p - p ' . Пусть р - произвольный тензор. В силу сепарабельности пространства Т в нем существует счетное всюду плотное множество. Известно [1], что для пространства L ₂( V ) таковым является в частности множество N непрерывных и непрерывно дифференцируемых в ( V + Г ) функций. Следовательно, множество М – тензоров с компонентами из N счетно и всюду плотно в T . Отсюда тензор р можно приблизить элементами из М , т.е. ( p _X , 4 ) ^ ( p , 4 ) ( p _X е M , 4 - любой тензор из T ). Ясно, что p _X = p X + p X , p ^ е T 1 , p X . е T ₂. Пусть ^ е T 1 . Тогда ( p _X , 4 ) = ⁽ p X + p X , ^= ⁽ p X , ^{4 )}^ ( p ' , 4 ) , т.е. последовательность p X сходится по метрике пространства T к элементу p ' е T 1 , так как подпространства Т 1 и T ₂ содержат все свои предельные точки. Отсюда ( p , 4 ) = ( p ' , 4 ) и ( p , 4 ) - ( p ' , 4 ) = 0. Следовательно, ( p - p ' , 4 ) = 0, т.е. p - p ' е T 2 .

Аналогично изложенному выше введем на элементах L^t ₂ ( V ) энергетическое пространство H(V ) положительно определенного оператора C ( C = S ^{- 1}), определив скалярное произведение и норму по формулам

( e , 9 ) _н = [ C -- e , 9 ] = J 9 -- C -- e dV , |e| H = ( e , e ) _H , e , 9 е L 2 (V ).

V

Гильбертовы пространства T и Н линейно изометричны в силу их сепарабельности и бесконечномерности [8]. Оператором линейной изометрии, отображающим Н на T , является тензор C . Действительно, пусть e е H , p = C -- e е T . Тогда отображение Н в T осуществляется с сохранением нормы

( p , p ) = ( C - - e , C -- e ) = [ S -- C - - e , C -- e ] = [ e , C -- e ] = ( e , e ) _H .

Очевидно, что оператором линейной изометрии, отображающим Т на Н , является тензор S . Применяя теперь оператор S к элементам подпространств Т ₁ и T ₂ , находим, что эти подпространства линейно изометричны подпространствам

H 1 = { e ' ; e ' = def u } , H 2 = { e" : e ''= S -- p" , p" e T₂ } и Н = Н 1 Ф Н 2 . Заметим, что элементами подпространства Н ₁ являются тензоры деформаций, удовлетворяющие условиям совместности (Jnk e ' = Jnk def u = 0 [10], Jnk- оператор несовместности). Элементами подпространства Н ₂ являются тензоры собственной несовместной деформации, которые вызывают появление полей самоуравновешенных напряжений и связаны с этими напряжениями непосредственно законом Гука. Из данных рассуждений следует, что закон Гука в линейной теории упругости ( p = C -- e, e = S -- p ) осуществляет линейную изометрию между пространствами тензоров деформаций и тензоров напряжений и наоборот.

Ортонормированные базисы

Так как подпространства полного сепарабельного гильбертова пространства сами являются полными сепарабельными гильбертовыми пространствами, то в них существуют ортонормированные базисы [8]. Построим такой базис в подпространстве Н 1 . Рассмотрим сначала пространство L 2 ( V ) и представим его суммой подпространств

L 2' = { u" : u ''= A + Л г } ,

L 2 =) u '

: J u ' dV = 0, V

J r x u ' dV = 0 > v

, где A – произвольный

постоянный вектор, г(x1, x2, x3) - радиус-вектор переменной точки области V , косой крестик означает векторное произведение векторов, Л - кососимметричная матрица с постоянными компонентами Л11 = Л 22 = Л33 = 0, Л12 = -Л 21 = у , Л31 = -Л13 = в ,

Л ₂₃ =-Л ₃₂ = а . Подпространства L 2 , L 2 замкнуты своими предельными точками.

Элементами подпространства L2 являются все нетривиальные решения уравнения def u =0, т.е. векторы жесткого смещения тела V. Элементами подпространства L2

являются векторы перемещений точек тела V , главный вектор и главный момент которых равны нулю (исключается жесткое смещение тела) и которые связаны с деформацией объема V по правилу ε = def u (производные здесь понимаются в обобщенном смысле). Таким образом, оператор def отображает элементы из L 2 в подпространство Н ₁ .

Подпространства L" и L 2 ортогональны. Действительно

( u",u ' ) = J ( A + Л г ) - u ' dV = A - J u ' dV + у J ( u ' x ₂ - u 2 x 1 ) dV +

VVV

+ p J ( u ' x 1 - u ' x ₃ ) dV + a J ( u 2 x ₃ - u ' x ₂ ) dV = 0

VV

(в силу равенства нулю главного вектора и главного момента вектора u ' ). Кроме того, каждый элемент из L 2 единственным образом представим суммой u = u ' + u '' .

Достаточно за u '' взять вектор A + Л г , где A и Л - решения уравнений

A J dV = J u dV , J г x Л г dV = J

г x u dV . После этого u ' = u

- ( A + Л г ) . Итак L 2

= L 2 Ф L 2' .

VV VV

Возьмем теперь в Lv2 (V ) некоторую последовательность линейно-независимых векторов uk (k = 1,2,...). Каждый вектор единственным образом представим суммой uk = u k + uk, uk e L2', uk g L2 . Действуя на элементы исходной системы оператором def, получаем def u k = def u k + def u k = ek = def u k, где в силу линейности оператора def последовательность е’к является системой линейно-независимых элементов подпространства Н1 . Применим к ней процесс ортогонализации Шмидта [8]. Полагаем       ю1 = е‘, к1 = ю1/||ю1|\ , к-1

^ю к = e k ^- Z ( e k , ^к n ) H ^к n , ^к к = ^ю к /I^ю А_н , ^к >  ¹¹ Полученную ортонормированию n = 1

систему е к всегда можно достроить до ортонормального базиса подпространства Н 1

• [8] . Действуя затем на каждый элемент этого базиса оператором изометрии С , находим ортонормальный базис q k = C • - к к подпространства Т 1 .

Ортонормированные базисы в цилиндрических областях

Возьмем область V_r в виде длинного полого кругового цилиндра с внутренним радиусом а и внешним b . В частном случае а = 0. Пусть в V r задан линеал квадратично суммируемых функций, зависящих лишь от расстояния r от оси цилиндра ( а <  r <  b ). Тогда пространство L v (V r ) = L 2 ( а , b ) и скалярное произведение в нем равно b

(ф, ф) = 2л|ф(r)ф(r)rdr . Полагаем далее, что пространство L2 Vr) состоит из векторов, а направленных по радиусам цилиндра, причем их длина зависит только от r , то есть эти вектора имеют только одну радиальную компоненту из класса L2 (а,b) (остальные две компоненты равны нулю). Теперь пространство Н(Vr) состоит из диагональных тензоров с компонентами из L2(а,b), а именно:  e11 = e r(r), e22 = e 0(r), e33 = e z = 0 .

Это обусловлено тем, что оператор def отображает элементы из L v ( V. ) в подпространство Н 1 ( V_r ) . Действуя же на векторы из L v ( V r ) оператором def, записанным в цилиндрической системе координат, получаем e r = du/dr , e 0 = ur , e^>z = 0. Здесь и далее индексом r обозначаем радиальные напряжения и деформации, индексом 0 - тангенциальные, индексом z компоненты, направленные вдоль оси цилиндра, производная функции u ( r ) е L ₂ ( a , b ) в общем случае понимается в обобщенном смысле, т.е. функция v является производной функции u , если для произвольной бесконечно дифференцируемой в замкнутой области и равной нулю в окрестности ее границы функции ф ( r ) выполняется равенство ( u , ф Г ) = - ( v , ф ) , полученное интегрированием по частям выражения, стоящего слева.

Полагая, что тензоры C и S в объеме Vr однородны и изотропны, т.е. их компоненты с =М96 „ +ц(5„, Sj, + S„ S, ) Si„„ =-42ц(3^ + 2ц)]-1 SjS „ +(4ц)-1 (S, S,, +S, S,), где X = v E[(1 + v)(1 - 2v)]-1, p = E[2(1 + v)]-1 - коэффициенты Ляме, E, v - модуль Юнга и коэффициент Пуассона, Sj - символ Кронекера, определяющий единичный изотропный тензор второго ранга, i, j, m, n =1,2,3, получаем скалярное произведение и норму пространства Н(Vr) в виде

b

( е , е ) н ( v_r ) = 2 л [ { г r [ ( Х + 2 p ) e r +Х e 0 ] + ^ 0 [ Х e r + ( Х + 2 p ) e 0 ] } rdr ,

a

||е| |2 н ( v_r ) = 2 n J [ ( X + 2ц ) ( с 2

+ e_q ) + 2Xe _r e_q ] rdr .

a

Отметим, что компоненты тензоров, принадлежащих подпространству Н 1 (Vr), -суть деформации, имеют место при осесимметричном плоском деформированном состоянии цилиндрической области Vr . Квадрат нормы в выражении (4) определяет удвоенную потенциальную энергию цилиндрического тела единичной высоты.

Перейдем теперь к построению базисов в подпространстве Н 1 (Vr), используя схему, изложенную выше. Подпространство Lv2 (Vr) состоит из векторов с одной радиальной компонентой ur(r). Известно [8], что одной из линейно независимых систем функций одной переменной r , заданных в неодносвязной области Vr , является система

- 1   2    - 2

u_r : r , r , r , r ,...

Применяя оператор def и ортонормируя полученную линейно-независимую систему тензоров по методу Шмидта с использованием выражений (4), находим ортонормированную систему в Н 1 (Vr):к’,к2,... . Затем получаем ортонормированную систему в H 1(Vr): qk = C --кк. Выпишем компоненты нескольких элементов найденной системы

q ‘ r = q ‘ Q = c W ^{2n c (} b 2 ^-

0 2)) — 1 , c = E [ ( 1 + v )( 1 - 2 v ) ] ^{- 1};

qZ r =^- q 2 q =

- c ( 1 - 2 v ) ba ( r ² -^ 2п c ( 1 - 2 v ) ( b ² - а ² ) ) ;...

Третий компонент диагонального тензора определяем всегда q z =^v( q r + q Q ) .

по

(6) формуле

Дополним систему (5)   непрерывными,   кусочно-дифференцируемыми функциями специального вида, не изменяющими ее линейной независимости. Имеем ur : r,1,2 fzX(z)dz,r2,^-,Д- fz2X(z)dz,... r r                r2 r2

аа где функция X(r) принимает значения ноль или единица в заданных отрезках. Ортонормированная система в подпространстве Т1 (Vr ) имеет вид (компоненты соответствующих тензоров)

- a

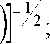
q ‘ r = q i q = ^c [ ^{2 n c ( b} 2

q 2 _r =- q 2 _q =- c ( 1 - 2 v ) bar ² [ 2 л c ( 1 - 2 v ) ( b ² - a ² ) ] ^/2;

^q 3 r = A 1

-

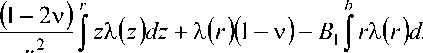
r +

a

a

+

2 B 2 ( 1 - 2 v ) b 1

2    J ~ r2      a r3

f z X ( z ) dz dr - ^2^, ^^v) f — x ( r ) dr

J                        r 2 Jr

V a          /                    a

^q 3 Q = A 1

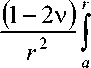
z X ( z ) dz + X ( r ) v

b

- B1 J rX(r)dr - a

-

2 B ₂ ( 1 - 2 v ) ^b b 1

r

B 2 ( 1 - 2 v ) ^b b 1

r ²

Л 2    2 V1

где B 1 = ( b - a )

a V a          J

Г b

r ²

J - ^{x (} r ) dr ,... ' r

a            _

( b A

B ₂ = a ² b ² B 1 , A 1 = 2 c 8 n c ( 1 - v ) j r X ( r ) dr 1 - 2 B 1 j r X ( r ) dr _             a V a /

.

Пусть a = 0 (область Vr - сплошной цилиндр). Тогда ортонормированный базис строим на основе последовательности ur :r,r2,r3,...                                            (7)

Производя необходимые действия, получаем компоненты тензоров базиса в T ₁ ( V_r ) :

q ³ r = q i e = ^{c ( b} V2k c ) 1 ;

q 2 r = M 1 ^{[( 2 -v) r - b} ] , q 2 e = ^M 1 ^{[( 1 + v) r - b ]} ,

M 1 = c ( b ² д/2 n c ( 1 - v ) / 2 ) ;

q ³ r

= M ₂

( 3 - 2 v ) r ² - 5 b ( 2 -v ) r + 5 b ²

^q 3 0 = M 2

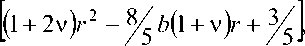
M 2 = c ( b 3V 2 n c ( 1 -v ) 275 ) ;

Дополним систему (9) непрерывными, кусочно-дифференцируемыми функциями специального вида. Имеем

2r3 r ur : r,— [zX(z)dz,r2,—- [z2X(z)dz,...

r ₀ r ₀

После выполнения необходимых действий находим ортонормированную систему тензоров в T1 (Vr) , компоненты которых q3 r = q ‘o =c

(b V 2n c) ;

q 2 r = A 2

- ——^—- j z X ( z ) dz + X ( r )( 1 - v) —у j z X ( z ) dz ] , r 2     ₀ b 2 ₀

q 2 0 = A 2

1 - 2 v r _r ^{2 j} r ₀

v

-

1 ^b

— j z ^X( z ) dz ^] , b ₀

b

/

b

b                b D

A ₂ = 2 c 8 n c ( 1 - v ) j r X ( r ) dr 1-- ^ j r X ( r ) dr

; ...

V

J

И, наконец, возьмем линейно-независимую систему

u_r : r , { a 1 r ,0 <  r <  a 1 ; a 1 ³ r

1 , a 1 <  r <  b }, { a 1 r , 0 <  r <  a 1 ; r ², a 1 <  r <  b } ...

Ей соответствует ортонормированная система тензоров из T ₁ ( V_r ) с компонентами q ³ r = q ‘ 0 = ^{c ( b} V2k c ) 1 ;

q2r = q2o = A3, 0

A4 = bc[2nc(b²- a²)+ 2a 14 (1 - v)] ^/2, A₃= A4a 1 (b² - a2 )/b² ;

q3r = q3o= 0 0 < r < ai, q‘r = A5 [(2 - v)r - b - b2a 12 (1 - 2v)(b + a1) 1 r2 - a 12 (b + a 1) 1 ]

qso = A5 [(1 + v)r - b + b²a2 (1 - 2v)(b + a 1) ¹r²- a1 (b + a 1) ¹] a1< r< b,

A5 = c {nc (1 -v)[0,25(b⁴- a⁴)-2 b²a1²(b - a 1)/(b + a 1)]} ^Z ;...     (10)

Метод ортогональных проекций

Рассмотрим сначала систему уравнений линейной теории упругости (2). Очевидно, что ее решением является некоторый тензор напряжений p'е T1, удовлетворяющий условиям V- p'= f, n • p'= t (f, t - заданные системы векторов, главные вектора и главные моменты которых равны нулю). Найдем коэффициенты разложения этого тензора в ряд Фурье по ортонормальному базису qk подпространства T₁ . Применяя формулу интегрирования по частям Остроградского-Гаусса, находим

⁽p'^,qk)=J p'S • -qkdV =J p'^-edV = J p' • •def ^ukdV =

V

V

V

= ^-J^V-p'^-u k

V

dV + Jn • p' • ukdr = -Jf • u_kdV +Jt • ukdr,

г

V           г

где uk - непрерывные и непрерывно-дифференцируемые функции из L2(V). Если f е L2 (V), а заданный на поверхности Г вектор t суммируем с квадратом по Г, то интегралы в правой части данного равенства существуют. Тогда обобщенное решение системы (2) представляется в виде ортогонального (в энергетическом пространстве) ряда с вычисленными коэффициентами Фурье

ГО

го

/

p^E^qk)qk = Е ^-J^f•^u*^{dV +}Jt•^uk^ qk•

k=1

^k=1 V V            г у

Этот ряд в силу полноты пространства T сходится как в энергетической метрике, так и в метрике исходного пространства L^t₂ (V ) [1].

Полученное решение является единственным. Действительно, пусть тензоры o1, ст'₂е T1 - два решения системы (2). Тогда о = o' - о2 е T1 также является решением. Однако V•o = 0, n ^о = 0 и, следовательно, ое T₂, т.е. ое T1 n T₂. Но T1 nT₂= 0. Отсюда о = 0 и о₁= о ₂ .

Далее пусть p* - любой тензор, удовлетворяющий уравнениям равновесия и граничным условиям задачи (2). Тогда p *- p' = q''е T2 и (p *, q k )=(q " +p', qk) = (p', q k). Отсюда тензор p', решающий задачу (2), есть проекция тензора p* в подпространство T1. В этом заключается смысл формулы (15). Так как p *- p' е T2, то (p', p *- p' )= 0 и |p *|| = |p' ||2 +1p* - p'|| > ||p' ||2. Данное неравенство выражает принцип Кастильяно: из всех тензоров, удовлетворяющих уравнениям равновесия и краевым условиям, заданным в напряжениях, наименьшую потенциальную энергию деформации сообщает телу тензор упругих напряжений [1]. Из приведенных рассуждений следует, что формула (11) фактически решает задачу о минимуме функционала p∗ - σ′ при заданном тензоре p ∗ , т.е. из всех значений σ′ ∈ T1 минимум этому функционалу доставляет тензор p ′ – решение задачи (2).

Отметим, что формула (11) позволяет находить, по крайней мере приближенно, так называемые слабые решения в тех случаях, когда непрерывных и непрерывнодифференцируемых решений не существует. При этом уравнения равновесия и условия совместности для соответствующего тензора деформаций удовлетворяются только в обобщенном смысле, а компоненты вектора перемещений могут иметь только первые обобщенные производные.

Перейдем к решению краевой задачи (3). Применяя оператор изометрии S к определяющему соотношению, получаем равенство e′′ = e′ - ε^∗, где e′′ ∈H₂ (p′′ ∈T₂), ε^∗∈H , e′ ∈H₁ – тензор совместной деформации. Найдем ортопроекции тензора ε^∗в подпространства H₁ и H₂ . Имеем e′ = Y₁ε^∗∈H₁, e′′ = Y₂ε^∗∈H₂ , где Y₁ , Y₂ – соответствующие операторы ортогонального проектирования (ортопроекторы). Тогда ε′ + ε′′ = Y₁ε^∗ + Y₂ε^∗ = (Y₁+ Y₂)ε^∗ = ε^∗(Y₁+ Y₂= J, J – единичный оператор). Отсюда e′′ = e′ - ε′ - ε′′ . Очевидно, что данное равенство может быть выполнено, если e′ = ε′ . Следовательно, e′′ = -ε′′ .

Применим теперь оператор изометрии C к разложению тензора ε ^∗. Получаем C ⋅⋅ε^∗ = C ⋅⋅ε′ + C ⋅⋅ε′′ или σ^∗ = σ′ + σ′′ , где σ^∗∈T, σ′ ∈T₁, σ′′ ∈T₂ . Очевидно, что

σ′ = P₁σ^∗– ортопроекция тензора σ^∗в подпространство T₁ , σ′′ = P₂σ^∗– ортопроекция в подпространство T₂ (P₁ , P₂ – соответствующие ортопроекторы). Отсюда p ′′ = C ⋅⋅e′′ = -C ⋅⋅ε ′′ = -P₂σ′′ . Таким образом, решением задачи (3) является взятая со знаком минус проекция элемента σ^∗∈T (σ^∗ = C ⋅⋅ε^∗) в подпространство T₂ . При этом совместные деформации, возникающие в теле, определяются тензором e′ = S ⋅⋅P₁σ^∗. Отметим, что и в данном случае возможно нахождение слабых решений, т.к. никаких ограничений, кроме принадлежности пространству T , на тензор σ^∗не накладывается.

Приведем некоторые следствия, вытекающие из полученного результата. Во-первых, зачастую удобнее находить решение задачи (3) в следующем виде:

p′′ = -P₂σ^∗ =-(J-P₁)σ^∗ = P₁σ^∗ -σ^∗ =∑(σ^∗,q′_k)q′_k -σ^∗,        (12)

n=1

т.е. сначала осуществить проекцию тензора σ^∗в подпространство T₁ .

Во-вторых, если ε ^∗∈H₁ , то в теле возникают деформации ε′ = ε^∗без образования напряжений. Если ε^∗∈H₂ , то в теле возникает самоуравновешенное поле напряжений без образования совместных деформаций, т.е. без изменения геометрии тела.

Напряжения в цилиндрических телах при плоской деформации

Рассмотрим несколько примеров применения изложенного метода ортогональных проекций.

Задача Ляме. Решим задачу об определении напряжений в толстостенной трубе. На внешней границе с радиусом b заданы одинаковые векторы внешних сил, имеющие одну направленную к центру трубы радиальную компоненту (- t ) (равномерное внешнее давление). Внутренняя граница с радиусом a свободна от нагрузки. Объемные силы отсутствуют.

Для более эффективного применения методики желательно на начальной стадии, используя внешние признаки задачи, сделать некоторые правдоподобные допущения относительно перемещений. Это позволит построить в подпространстве T₁ такой базис, при котором ряд Фурье, получающийся в результате операции проектирования, сходился бы достаточно быстро. В данном случае вектор перемещений имеет одну радиальную компоненту, зависящую только от расстояния от оси трубы. Эта компонента может быть представлена непрерывными и непрерывнодифференцируемыми необходимое число раз функциями от r , в том числе и обладающими сингулярностями при r = 0 .

Следовательно, можно воспользоваться последовательностью (5), элементы которой обладают указанным свойством. Базис в подпространстве T1(Vk), соответствующий последовательности перемещений (5), задан выражениями (6).

Для применения формулы (11) необходимо перейти от базисных напряжений к перемещениям, определяя из закона Гука деформацию eQ = E-1 [qQ(1 - v2)-qrv(1 + v)] и затем перемещение и = eQr из одного из соотношений Коши. В результате получаем и 1 = rk 1, и 2 = r 1 к 2

,...,

где к 1 = [2п c (b²

2 a

к₂= ba [2nc (1 - 2v)(b²

2 a

Теперь по формуле напряжения

(15) с использованием выражений (6) определяем

искомые

or = m1 q‘_r + m₂q2_r = -tb²(b²

^oQ = m q‘_e + m 2 q 2q = ^{- tb 2 (b 2}

a²)^-1(1 - a²r"2

-

a²) 1 (1 + a²r

-2

), ),

2n где m1 = -Jtbk 1 bdф,

Отметим, что

Oz = v(o'_r + oQ) = -2v tb²(b²

2n

-

a 2 Г

m₂= - Jtb^-1к₂bdф, - коэффициенты Фурье.

коэффициенты m3 = 0 и данное решение являются

точными,

совпадающими с хорошо известными в литературе [11].

Закалочные напряжения. Рассмотрим длинный сплошной цилиндр с радиусом основания b . Пусть в результате закалки в нем реализовано поле первоначальных

(собственных) деформаций, определяемых тензором е* с компонентами вГ = eQ = eZ ={ур(b - a 1 )1 (r - a1), a1 < r < b, 0, 0 < r < a1} (закалка по линейному закону до радиуса a1). Здесь р - объемное содержание новой фазы материала, возникшей в результате закалки, в поверхностном слое, у - параметр свободной структурной деформации новой фазы. Подставляя тензор е* в физические соотношения закона Гука, находим тензор о* с компонентами о* oQ о* ={ур E (1 - 2v)-1 (b - a 1 )-1 (r - a1), a1 < r < b, 0, 0 < r < a1}.

Можно предположить, что в этом случае радиальные перемещения непрерывны, но их производная терпит разрыв при r = a1. Отсюда целесообразно использовать последовательность (9) и базис (10). Производя необходимые действия по формуле (12) с учетом выражения (4), находим o'r = oQ = E'b>33 - a1/3 + a13 /бb2), 0 < r < a1;

о'r = E'[(b - r)/3 + a 13 (b-2 - r)/6], oQ = E'[(b - 2r)/3 + a13 (b+ r ^2)/б], a1 < r < b .

Если торцевые концы цилиндра свободны от нагрузки, то возникают еще напряжения gZ =o" +Oq = {2E'b3 -aJ3 + a13/6b2) 0 < r < a 1;

E.Г(2b - ³r)/ + ay 1 a 1 < r < b }.

3 b

Здесь E' = урE[(1 - v)(b - a 1 )]^-1.

Отметим, что остальные члены ряда в формуле (12) равны нулю и данное решение является точным.

Полагая a1 = 0 (закалка на всю глубину), находим следующие выражения для напряжений:

cr = Еур[3b(1 - v)]-1 (b - r),    cQ = EYp[3b(1 - v)-1 Jb - 2r), g'Z = Eyp[3b(1 - v)]-1 (2b - 3r)

Заметим, что тот же результат получается, если спроектировать тензор ст* при а1 = 0 в подпространство T1 (V_r), используя базис (8).

Последовательность перемещений (7) и базис (8) также можно применить для решения задачи с первоначальными деформациями еГ = ar, sQ = вr, sZ = vr (0 < r < b, а, в, v - const). Производя необходимые действия, получаем с r = n (R - r), oQ = n (R - 2r), где n = -E [3(1 - v2 )]-1(a- Зв-yv).

Пусть теперь закалке подвергается труба с внутренним радиусом a , причем закалка осуществляется изнутри на всю толщину. Имеем sr =sQ =sZ =yp(b - r )(b - a)-1,

^G*r =^CQ =^GZ =YP^{(b - r)(b -}a^)-1(1^{- 2v)-1}.

В этом случае целесообразно использовать последовательность перемещений (5) и базис (6). Используя формулу (12), находим стr = 11 r +12r -13, ctQ = 211 r -12r -13, где 11 = ур El 4, 12 = ур Eb 2 a 214, 13 = YPE (b 2 + ba + a 2 ), 14 =[3(1 -v)(b - a )]-1.

Заметим, что приведенные решения совпадают с решениями данных задач, полученных традиционными методами.

Приведены основные положения метода ортогональных проекций решения краевых задач линейной теории упругости при заданных поверхностных и объемных силах. Отмечена возможность получения слабых решений.

Работа выполнена в соответствии с программой интеграционного проекта с СО РАН.