О решении линеаризованной задачи движения вязкой теплопроводной жидкости в термоупругой трубке с помощью несвязанных уравнений Кирхгофа

В работе [1] описана математическая модель, позволяющая рассчитывать стационарные температурные поля и поля упругих колебаний в термоупругой трубке и вязкой теплопроводящей сжимаемой жидкости при условии связанности упругих и тепловых процессов. При решении задачи о движении жидкости в трубке использовалась система связанных уравнений Навье—Стокса и теплопереноса. И если в случае, когда жидкость занимает неограниченное пространство, решение связанной системы уравнений получается достаточно просто [2, 3], то в случае, описанном, например, в [1], аналитическое решение такой системы становится крайне проблематичным в силу существенного различия краевых задач для упругих и температурных компонентов поля. Отметим, что в [2, 3] упругие и температурные компоненты поля описывались через единые собственные функции оператора Лапласа. В рассматриваемой в [1] постановке задачи такой подход несправедлив в силу связанности продольных и поперечных компонент упругих полей (на границах сред происходит взаимная трансформация продольных волн в поперечные и обратно).

Существует, однако, возможность перехода от системы связанных уравнений второго порядка для потенциальных составляющих поля и температуры в упругой трубке и в жидкости к одному уравнению — т. н. уравнению Кирхгофа [2]. Это уравнение относительно либо температуры, либо скалярного потенциала скорости жидкости (деформации упругого твердого тела). Уравнение

Кирхгофа уже является уравнением четвертого порядка (в полном согласии с принципом сохранения трудностей).

Представляет интерес получение системы несвязанных уравнений типа Кирхгофа в такой мультифизичной задаче, каковой является движение вязкой теплопроводной жидкости в термоупругой трубке.

ПОСТАНОВКА КРАЕВОЙ ЗАДАЧИ

Таким образом, необходимо получить уравнение Кирхгофа линеаризованной задачи для случая вязкой теплопроводной жидкости, находящейся в термоупругой трубке.

Напомним постановку краевой задачи о течении вязкой теплопроводной жидкости в термоупругой трубке [1].

Пусть в состоянии равновесия (покоя) жидкость характеризуется параметрами (используем индекс 0): v ₀ , p ₀ , ρ ₀ , T ₀ (соответственно скорость, давление, плотность, абсолютная температура). Возмущенное состояние будем характеризовать штрихованными добавками с порядком приближения, равным количеству штрихов, а именно: V = v 0 + v ' + v "+ ... , p = p 0 + p ' + p "+ ... , p = p 0 + + p '+ p "+ ..., T = T 0 + T ' + ... . Аналогично и для вводимых ниже параметров у = Y 0 + Y ' + — , а = = а 0 + а ' + ... , п = П 0 + П ' + ... , £ = £ 0 + £ ' + ... и ^т . Д.

В работе [3] приведена стандартная линеаризованная система уравнений Навье—Стокса д-р = CO2P0 ( a 0    -V-v'),(1)

дt     у о V    дt po    = -Vp'+ По Av'+1 ^о + П0- ) W - v',(2)

дtV p + poV-v' = 0.(3)

д t

В [1] приведено также линеаризованное уравнение теплопереноса, полученное изначально в [3],

_{A T} •- ± ^{9 T}' = - ^a o ^T o ⁹P' ,

Xо дt       Ko дt ’ однако здесь представим его несколько в другом виде, следуя методике преобразования общего уравнения теплопереноса, приведенной в работе [2]. Линейная часть общего уравнения теплопере-носа [4, с. 272]

— + v -V s 1 = 7' dv- + V-(KV T) дt         ) дxk v ’ в сжимаемой жидкости имеет вид

_Q _     1 (д V 0     _                  ,

Здесь a =—^p) — термодинамический коэф-

Ж „             _{o         R} 1 (д V 0

фициент расширяемости; в =--—   — тер- v Vsp) T модинамический коэффициент сжимаемости; cp , cV — удельные теплоемкости при постоянном давлении и объеме соответственно.

Из линеаризованного уравнения неразрывности

Pp'

(3) имеем =—-p- p V - v'. С учетом этого послед-д t нее выражение в линеаризованном виде запишется

T ds       d T' Txv , pT — = p cv„---+ -0—0 V- v'.

P 0 0 d t     0 V 0 d tp

В итоге уравнение теплопереноса в линейном приближении примет вид p0cV0 ST    1 Toao r-7

A T---=V -

^K o 61   ^K o P o

Это выражение совпадает с уравнением (2.148) работы [2]. Положив c_V = c_p I у , а кроме того, исполь-

„ ds

P o T o - = K o A T ', д t

зуя выражение [2, с 87]

Tα cp - cV = cV ( у -1) = — т. к. все отброшенные члены носят порядок выше первого. Здесь s — энтропия единицы массы жидкости; κ — коэффициент теплопроводности

,    ( Pvi д vk 2    д vz 0    s д vz жидкости; 7= n    + -rk-^5lk-) 1 + ^5lk-P —

Vdxk дxi 3   дxl)      дxl вязкий тензор напряжений; η , ς — соответственно коэффициенты сдвиговой и объемной вязкости; c0 — равновесная скорость звука в жидкости.

Представим энтропию s в переменных T , V

(здесь V — удельный объем, или объем единицы

1 , .    ( дs 0       ( дs 0       _ массы V = —): ds = — dT + — dV . Тогда p VpT ) V     Vp V ) T

Ta     c_v ( у ^- 1 )

и следующее из него равенство -- = p —-----

βα

перепишем последнее уравнение теплопереноса в виде

A T' — ^{P T}- = ^{( Y 0} 1 ) V- v '.

X 0 у 0 St ^a o у o X o

дs     ((Ps 0 dT (ds 0 dV° pT— = pT — —+— - .

dt _vvst )„ dt vsv)_T dt)

Это выражение уже совпадает с полученным иначе выражением (12) работы [3] с точностью до гармоничности процесса в указанной работе.

Для сокращения выкладок необходимо представить вектор колебательной скорости v' в виде суммы потенциалов v' = v' l + v' t = gradФ + rotT. (5)

Учитывая соотношения [5, с. 185–187]

T ( д s 0          ( д s 0    ( д p 0

T — = c„ ,  — = —— = a I в , запишем

U T ) V   V (д V ) T Vd T ) V предыдущее выражение в виде

Здесь v ' _l , v ' t — продольная и поперечная составляющие колебательной скорости соответственно; Ф , T — ее скалярный и векторный потенциалы. Подставляя (5) в (1), (2), получаем:

sp _ c o p o L, ^a n st     у o V

д T '

д t

-

АФ

д s     д T   ax д V     д T pT— = pcv — + pT--= pcv — д t     V д t       в д t      V dt

—

t— a д р рв д t

.

и

dVO „    „ f 77nK po "^- = -Vp'+ Пo VAФ + ko + 40 IVAФ ,

P t                         V 3 )

или дФ   Л   4п

Р о — = ^—Р ' + 1 ^? о + Л 1 ^АФ . д t I        3 )

Из выражения (7) следует полезное выражение для p '

Уравнение (10) в гармоническом случае преобразуется к виду

А T '+ i®-¹- T' = ^{( Y о} - 1 ) АФ .

χ ₀ γ ₀      α ₀ γ ₀ χ ₀

Из (12) находим f ,4% I дФ р' =к о +    |АФ —Ро —.

V 3 )          д t

Дифференцируя (7) по t и подставляя в него зна- дР'

чение из (6), получаем д t

— АФ + γ ₀

_{ς 0 +} 4 η ₃0

ρ ₀

—АФ д t

—

д ² Ф "a t ²"

c ²

=-- а о

γ ₀

д T' д t

Вводя обозначение

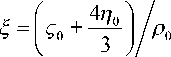
где ξ —

АФ = — в Ф — i ^^a^ T '.

1       _{β 3}

После подстановки этого выражения в предыдущее получаем

А T ' + в ₂ T ' = ⁽ 1 - ^{Y о} ) ^{в 1} Ф .          (13)

α ₀ χ ₀ γ ₀

Здесь приняты обозначения:

P i = Y о ® 2 / ( c о² Р з ) ,

совокупный коэффициент вязкости, перепишем последнее уравнение в виде

в 2 = i ®

Р з + Y — 1 χ ₀ γ ₀ β ₃

f1+Aа-Ф = „одП.

_V    c о д t J      c о д Р      д t

^р з = ^{1 —} i ту о

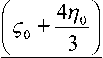
ρ 0 c 0 ²

Наконец, подставляя в (4) выражение (5), получаем

А T'— — = ^{( Y о} 1 ) АФ . Х о Y о ^д t ^а о Y о Х о

После применения операции rot к обеим частям (2) получаем стандартное уравнение для векторного потенциала в вязкой жидкости

Выражения (12), (13) представляют собой связанную систему уравнений относительно температуры T ' и скалярного потенциала Ф в гармоническом случае и совпадают с выражениями [3, (14, 15)]. Получим из них уравнения Кирхгофа для обеих переменных. Для скалярного потенциала Ф

(А + Р2 )(А + Р1 ) +

ат

Р о — = П о А - . д t

i та о ( 1 ^— Y о ) ^р 1 β ₃    α ₀ χ ₀ γ ₀

Ф = о

и для температуры

Выражения (9)–(11) полностью описывают в линейном приближении поведение вязкой теплопроводной жидкости. Причем связанными остаются выражения (9) и (10) для скалярного потенциала Ф и температуры T '. Векторный потенциал Ψ подчиняется автономному параболическому уравнению (11).

Далее получим уравнения Кирхгофа. Вначале рассмотрим более простой гармонический случай. Пусть имеет место гармонический процесс с фактором e ^{— i m t} (далее фактор e ^{— i m t} опущен и выписаны выражения для амплитуд соответствующих величин при сохранении обозначений). Выражения (9)–(11) преобразуются к виду

АФ + в Ф = — i^ T '.

1         _{β 3}

(А + Р1 )(А + Р2 ) +

iтао (1—/о1в11T' = о

β ₃    α ₀ χ ₀ γ ₀

получаем в силу коммутации операторов ( А + Р 1 ) и ( А + Р ₂ ) совершенно идентичные уравнения Кирхгофа для гармонического случая.

Для (11) в гармоническом случае получаем уравнение [1, 2]

( А + к з² ) - = о ,      к з = 1 +^ .          (16)

v

Здесь 5v = ^2 v _о / т — глубина проникновения вязкой волны.

Для связанных уравнений термоупругости в упругой теплопроводящей трубке имеем [1, 6]

A T + i to I— + 0l T ' = i w 0 ( k '1) ф ,   (17)

Аф + ( k 'i ) ф = —— T '.         (18)

A + 2 Ц 1

Здесь введены обозначения: ϕ , ψ — скалярный и векторный потенциалы смещения в трубке; λ1 , µ1 — упругие модули Ламе для трубки; ρ1 — ее плотность; Г = (зА + 2pi )at — термомеханическая постоянная; αt — коэффициент линейного терми- ческого расширения; Л = К1 — коэффициент тем-cε пературопроводности; κ1 — коэффициент теплопроводности трубки; cε — удельная теплоемкость при постоянной деформации; 0 = —0 ; Т0 — рав-κ1

2 2ω новесная температура тела; (ki) = --------------.

( A + 2 M i ) / P i

Вводя обозначение в4 = i to

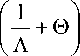
перепишем (17) в виде определяют оба потенциала колебательной скорости и температуру в жидкости, а (19)–(21) определяют оба потенциала смещения и температуру в твердом теле. К уравнениям (14)–(16), характеризующим поля в жидкости, необходимо добавить выражение, определяющее давление. Для этого преобразуем уравнение (8) применительно к гармоническому случаю:

P ' =

4 n I .

? о + — |AФ + i toP o Ф .

При решении несвязанных уравнений (14)–(16), (22), а также (19)–(21) необходимо учитывать механические и тепловые краевые условия задачи, подробно описанные в [1].

ОБЩИЙ СЛУЧАЙ ВРЕМЕННÓЙ ЗАВИСИМОСТИ ПРОЦЕССА

Исходными для дальнейших преобразований примем уравнения (9) и (10).

Введем следующие дифференциальные операторы:

Д( « Х , d t ) =

fi+ ^Y4 1V ' '" _v c ₀² d t J c ₀² d t²

L 2 ( d x , d t ) = A-

i d

X 0 Y 0 ^d i t

A T ' + в ₄ T ' = i to 0 ( k ' 1 ) ² ф .           (17а)

На основании выражений (17а) и (18) получаем для упругой трубки уравнения типа Кирхгофа:

( ^{A +} ( ^k ' 1 ) ) (^{A + в} 4 ) -

- i to 0 ( k '₁ ) 2

Γ

A i + 2 ^ i

T ' = 0,

L3(dt) a0    , dt

L 4 ( d x ) = ^ ^) A . α ₀ γ ₀ χ ₀

Тогда уравнения (9) и (10) перепишутся в операторном виде так:

L i ( d x , a _t ) Ф= L з ( д _t ) T ' ,                  (23)

(^{A+ в} 4 ) ( ^{A +} ( ^k ' i ) ) -

-

Γ

A + 2 M _i

i to 0 ( k '_i ) 2 ф = 0.

Для векторного потенциала ψ легко получить [1]

( A + k '_з ² ) v = 0 ,

k '₃²

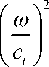
Здесь c = — — скорость поперечных колебаний ρ 1

в упругом теле.

Таким образом, несвязанные уравнения (14)–(16)

L 2 ( d x , d _t)T ' = L 4 ( d x ) Ф .                  (24)

После умножения уравнения (23) на оператор L ₂ ( d _x , d _t ) слева получаем (очевидно, что операторы коммутируют вследствие постоянства коэффициентов)

L 2 ( d x , a t ) L i ( d x , a t ) Ф = L 2 ( d x , a t ) l з ( а t ) t ‘ =

= l з ( а t ) l 2 ( a x , a t ) t ‘ = l з ( а t ) l 4 ( d x ) Ф .

Тогда окончательное уравнение типа Кирхгофа для скалярного потенциала имеет вид

[ L 2 ( d x , a _t ) L i ( d x , a _t ) - L з ( д _t ) L 4 ( d x ) ] Ф = 0.      (25)

Аналогичным путем получаем уравнение типа Кирхгофа для температуры T ' :

L1(∂x,∂t)L2(∂x,∂t)T'=L1(∂x,∂t)L4(∂x)Φ= =L4(∂x)L1(∂x,∂t)Φ=L4(∂x)L3(∂t)T', или в компактном виде

[ L 1 ( ∂ x , ∂ t ) L 2 ( ∂ x , ∂ t ) - L 4 ( ∂ x ) L 3 ( ∂ t ) ] T ' = 0 .      (26)

Дифференциальные операторы в (25) и (26) полностью совпадают, вследствие того что составляющие их операторы являются коммутирующими. Отметим, что уравнения (25), (26) так же, как и в стационарном случае, имеют четвертый порядок по пространственной координате.

Таким образом, поле в жидкости полностью задается скалярным потенциалом, определяемым из (25), векторным потенциалом, определяемым уравнением (11), температурным полем, определяемым уравнением (26), и полем давления (8).

Рассмотрим уравнения типа Кирхгофа в нестационарном случае для упругого твердого тела. Общие уравнения термоупругости для твердого тела при отсутствии источников записываются так [6, с. 1, 24]:

∂ ² u

ρ _{1 2} = µ ₁ Δ u + ( λ ₁ + µ ₁) ∇∇⋅ u - Γ ∇ T ',

Δ T ' - ^{1 ∂ T '} =Θ∇⋅^{∂ u} . Λ ∂ t        ∂ t

Последние уравнения запишем через потенциалы ϕ и ψ (см. [1]):

1 ∂2ϕ Δϕ- cl2 ∂t2

cl ²

λ ₁ + 2 µ ₁ = , ρ ₁

Δ ψ - _c ¹ _t 2 ^∂ _∂ ² _t ^ψ 2 = 0 ,

ct ²

µ ₁ = ,

ρ ₁

ΔT'-1∂T'=ΘΔ∂ϕ. Λ ∂t∂

Поступая так же, как для

случая нестационар-

ного процесса в жидкости, имеем

[L6(∂x,∂t)L5(∂x,∂t)-L7L8(∂x,∂t)]ϕ=0,(27)

[L5(∂x,∂t)L6(∂x,∂t)-L8(∂x,∂t)L7]T'=0.(28)

Здесь операторы имеют следующий вид:

1 ∂ ²

L5(∂x,∂t) = Δ- 22

c ₁ ∂ t

L 6 ( ∂ x , ∂ t ) =Δ- ^{1 ∂} , 6 x t         Λ ∂ t

L 7 = Γ ,         L 8 ( ∂ x , ∂ t ) =ΘΔ^∂ .

∂ t

Таким образом, взамен связанных уравнений термоупругости выписаны несвязанные уравнения типа уравнения Кирхгофа для твердого термоупругого тела, позволяющие получить в нем все характеристики полей.

ВЫВОДЫ

Таким образом, получены несвязанные уравнения типа Кирхгофа, позволяющие решать связанные линеаризованные уравнения термоупругости для твердых тел и связанные уравнения системы Навье—Стокса для вязкой теплопроводящей сжимаемой жидкости как в стационарном, так и в нестационарном случаях. Уравнения записаны для скалярных потенциалов смещения твердого тела и скорости в жидкости, а также для полей температуры в твердом теле и жидкости. Полученные уравнения позволяют рассчитывать все нужные компоненты волновых полей в термоупругой твердой среде и в вязкой сжимаемой теплопроводной жидкости. Это предоставляет дополнительные возможности для расчетов указанных полей в упругих областях, контактирующих с жидкостью.