О решении одной сингулярно возмущенной начально-краевой задачи для линейного параболического уравнения

В работах [1,2] были изучены математические модели заполнения тонкостенных оболочек газом. Такие задачи возникают при исследовании технологических процессов производства, лазерных мишеней для инерциального термоядерного синтеза. [3-5]. В статье [1] поставленная задача, в безразмерных переменных сводилась к решению сингулярно возмущенного параболического уравнения для задачи Коши со специальными краевыми условиями. Решение строилось в виде асимптотического ряда. При этом автор ограничивался лишь первым членом ряда, для регулярной составляющей решения, пренебрегая пограпслойпой частью, учитывающей начальные условия. Оправданием применимости такого метода, являлся тот факт, что пограпслойпая составляющая быстро затухает и решение «забывает» начальные условия. В настоящей работе доказана, теорема, о существовании и единственности решения более общей задачи, чем та, что исследовалась в [1,2]. Построено решение ее нулевого приближения в виде суммы регулярной и погранслойной составляющей и дана, равномерная оценка, остаточных членов асимптотического ряда.

• I.    Постановка задачи

Рассмотрим центрально-симметричное параболическое уравнение с малым параметром е >  0:

ди 1 д / 2 ди \ е dt    r2 dr r dr ’           (1.1)

е >  0 , t >  0 , 0 < r 1 6 r 6 r 0 .

Граничные условия неоднородные:

и ( r о ,t ) = f ( t ) + p ( t ) , и ( r 1 ,t ) = p ( t ) .      (1-2)

Функция f ( t ) считается известной, а функцию p ( t ) следует определить. Уравнения для определения функции p ( t ) имеют следующий вид:

dp ⁽ t )       ^du ⁽ r i ,t )

= " ^щ - ^{p (0)} = b. ^,1-'*

Начальное условие

и ( r, 0) = U ( r ) .                 (1.4)

Будем предполагать выполненными условия согласования

U ( r i) = b, U ( r о) = b + f (0) .       (1.5)

В настоящей работе доказывается следующая теорема.

Теорема. Если функции f 0 ( t ) и U⁰⁰ ( r ) непрерывны и выполнены условия согласования (1.5), то найдется такое число е 0 >  0, что при 0 < е < е 0 решение задачи (1.1) - (1.4) существует, единственно и может быть представлено в следующем виде:

и ( r, t, е ) = и о( r, t ) + и 1( r, t, е ) + еи 2( r, t, е ) , P ( t ) = p о( t ) + ер i( t,е ) .

(1.6)

Функции р о( t ), и о( r,t ) являются решениями вырожденной задачи:

t

Pо(t) = b + “rо [ f (s) ds, (1.7) r о - r i и о (r, t )= p о (t) + rr ^ -rr11 f (t) .       (1.8)

Погранслойная функция и 1( r,t,е ) компенсирует невязку в начальных условиях:

, ,          2

^{и 1( r}'^{T ) =} ЩТ - 5) ^х

*Работа выполнена при финансовой поддержке АВЦП «Развитие научного потенциала высшей школы», проект 2.1.1/12136.

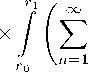
e

λ

2 n

λ ² n

τ

sin X n ( r i

— s ) sin X n ( r 1 — r )

x

x ( sU⁰⁰ ( s ) + 2 U⁰ ( s )) ds. (1 . 9)

Функции u ₂( r, t,e ), ц 1( t,e ) равномерно ограни

чены.                                     □

= —rU ( r ) + гц (0) + r 0 ——- f (0) = ф ( r ) . (2 . 6) r 1 — r 0

Вследствие условий согласования (1.5)

^{ф ( r} 0 ) = ^—r 0 ⁽ U ^{( r} 0 ) ^{— b — f (0))} = ⁰ ,       .   .

ф ( r 1 ) = r 1 ( U ( r 1 ) — b ) = 0 .

Упростим постановку задачи при помощи замены зависимых переменных:

v ( r, t ) = гц ( t ) + r 0 —--- - f ( t ) — ru ( r, t ) . (1.10)

r 1 — r 0

Уравнения (1.1) - (1-5) принимают следующий вид:

е § = drv + ^ t )+ er 0 y—; f' ( t ) ■  (I⁷')

v ( r 0 ,t )=0 , v ( r 1 , t ) = 0 ,             (1 . 8⁰)

dц ( t )

dt

= _ a dv ( r 1 ,t ) _     ar 0     f ( t )

r 1     dr       r 1 ( r 1 — r ; ) '

ц (0) = b, (1 . 9⁰)

v ( r, 0) = —rU ( r ) + rb + ——- f (0) .    (1 . 10⁰)

r 1 — r 0

• II.    Решение вырожденной задачи и уравнений погранслоя

При е = 0 мы получаем вырожденную задачу

Й =0 , v о ( r 0 ,t ) = 0 , v о ( r 1 ,t ) = 0 ,

∂r ²

^d-Y = — r H ra— - д f ( t ) • ц^ b

Начальное условие (1.10) в общем случае не может быть удовлетворено. Решение вырожденной задачи имеет следующий вид:

v 0 ( r, t ) = 0 ,

Положим в

t ц0(t) = b--^r0—- [ f (s)ds.

r 1 ( r 1 — r 0 )

(2.1)

уравнениях (1.7’) - (1.10)

Полагая в системе (2.3) - (2.6) параметр е = = 0, получаем систему для определения погранс-лойных функций:

dv    д2v, дт = dr2 ’ v(0’t)=0’(2.8)

v(r 1, t) = 0, v(r, 0) = ф(r), dz0^ = 0, z 0(0) = 0.(2.9)

dτ

Из уравнений (2.9) следует, что z ₀( т ) = 0.

Рассмотрим ортогональную на отрезке [ r ₀ , r 1] систему функций

^ n ( r )=sin X n ( r 1 — r ) , X n = nⁿ .    (2.10)

r 1 — r 0

Лемма 2.1. Если функция U ( r ) имеет непрерывную производную второго порядка, то решение смешанной задачи (2.8) имеет следующий вид:

v(r’T) = X ф e-nT sin Xn(r, — r), r 1 n                                  (2.11)

Y n =------- [( sU⁰⁰ ( s ) +2 U⁰ ( s ))sin X n ( r 1 — s ) ds.

r 1 — r 0

r 0

Функция v ( r, т ) имеет непрерывную производ-

„ Эй нуто dvr. причем

∞ dv = — X Yn e-X>.   □ (2.12)

∂r           λn n=1

Доказательство. Разложим функцию ф(r) по ортогональной системе (2.10). Так как ф(r0) = = ф(r 1) = 0 в силу (2.7), а в силу равенства (2.6) ф00(r) = —rU00(r) — 2U0(r). то т = t/e, ц (t,e )= ц 0( t) + z (t,e).       (2.2)

Тогда, система, уравнений (1.7’) - (1.10’) принимает следующий вид:

дТ = ^d_rvv ^{+ erz} 0 ^{( ет} ) ^{+ er} 0 r—rT ^f 0 ^{( ет} ) ,   (2.3)

v ( r 0 ,т )=0 , v ( r 1 ,т ) = 0 ,         (2.4)

df) = ear, z «»=0

∞ ф (r) = ^bk Vk(r) ’ k=1

v ( r, 0) =

b k =

r 1 — r 0

r 1

I ф ( s )sin X k ( r 1

r 0

— s ) ds =

r 1

-------—   ^{ф0 (} s ^{)cos X}k ⁽ r 1

(r1 — r0)Xk r0

— s ) ds =

r 1

₇-------—^   ф ( s )sin Xk ( r 1 — s ) ds = -^Yk,

(r1 — r0)X2k                                  X2k r0

Y n =

—2— / (sU00 (s) r 1 - Г о J r0

+ 2 U⁰ ( s )) sin X n ( r 1

— s ) ds.

Решение смешанной задачи (2.8) имеет вид ∞

v ( r, т ) = X Д e - ^x n ^T sin X n ( r 1 — r ) .     (2.13)

^~^ A ² n =1 ⁿ

∞

В силу неравенства. Бесселя ^2 y S <  ⁺ ^- а в n =1

∞ силу неравенства Коши V Yn < +ю- Следова-λn n=1 n тельпо, ряды (2.13) и (2.12) сходятся равномерно и справедлива, формула. (2.12). Теорема, доказана.

III. Доказательство теоремы существования и единственности решения интегрального уравнения для функции z ( т, е )

Положим

v ( r, т )= v ( r, т )+ w ( r, т ) ,   w ( r, 0) = 0 ,

w ( r о ,т ) = 0 , w 1( г,т )=0 .

(3.1)

Подставляя эти выражения в уравнения (2.3) -(2.6), получаем уравнения для функций w и z:

dw  d 2 w w = д7 — dr2 =

= — erz' (т) — er о r1—- f0 (eт), (3.2) r 1 — r о w (r о ,т ) = 0, w (r 1 ,т )=0, w (r, 0)=0, (3.3)

dz ( т ) = ea dw ( r 1 ,т ) _— ea dv о( r 1 ,т )

dт r 1 dr r 1 dr

Сведем задачу определения функции z ( т ) к решению интегрального уравнения. Для этого воспользуемся разложениями

r = ( r 1

∞

— r о) X T n sin X n ( r — r 1) , λ n

a n = ^{2(( —} 1) n ^r о ^{— r} 1) ,

(3.5)

Следовательно,

∞ w = —e(r 1 — rо) n sin Xn (r — r 1) x λn n=1 n

x

τ

I e^- n ^{( T}- ) z⁰ ( e ) de о

er о r 1 — r о

∞

X n=1

sin X n ( r — r 1) λ n

x

r — r ₁

∞

=X n=1

sin X n ( r — r 1) λ n

Запишем уравнение (3.2) в следующем виде:

dw  d2w дт dr2

∞

= —e ( r 1 — r о) z⁰ ( т ) X n s sin X n ( r — r 1) — n =1 ^Xn

er о r 1 — r о

∞ f0(eт) X n=1

sin X n ( r — r 1) λ n

τ

x

e ^x n ^{( T 5} ) f⁰ ( e^ ) de,

(3 . 6)

^{dw (} d’r’^T ) = —e ( r 1 — r о) X a n / e ^X n ^{( T 5} ) z ( e ) de— n =1 _о

er о r 1 — r о

∞ ^τ

^X n =1 _о

e -x n ^{( т} s ) f 0 ( e^ ) d^.

(3 . 7)

Так как

τ j e-xn(T-5)z0(^) d^ о

τ j e-xn(T-5) f0(e^) d^ о

⁶ X n "z - "'

⁶ X n "f",

(3.8)

то ряды в формулах (3.6) и (3.7) равномерно сходящиеся.

Подставляя (3.7) и (2.12) в формулу (3.4), получаем интегральное уравнение для определения (функции z ( т ):

^z 0 ^{( т} ) =

e ² a ( r 1 — r _о) r 1

∞τ an n=1   о

e^-x n ^{( т} - ⁵ ) z⁰ ( ^ ) d^—

e 2 r о a о r 1 — r о

∞ ^τ

^X n =1 _о

e ^x n ^{( T 5} ) f⁰ ( ee ) de—

^ea X Y n.' п т ^r 1 n =1 ^X n

(3 . 9)

Найдем уравнение для z ( т ). Так как z (0) = 0, то

τs

/ ds /

e^-x n ^{( s-5} ) z⁰ ( e ) de =

ττ

I z⁰ ( e ) j e^-x n ⁽ s ^-5 ) ds =

τ

= Xn / z ^{( e} ) о

1 —

e ^x n ^{( T 5} Г) de =

z ( e ) ( 1 — e^-x n ^{( т-5} ) )) + \                 / / о

+у z ( e ) e^-x n ^{( т-5} ) de = у оо

z ( e ) e^x n ^{( т 5} ) de,

ττ

/ ds!

e ^X n ^{( s 5} ) f 0 ( e^ ) d^ =

= А f ⁽⁰⁾

(¹ -

e

_λ 2 _{n τ}

τ

+ e j f ( e^ ) e^-X n ^{( T} — ⁵ ) d^.

Используя эти равенства, получаем выражение для z ( т ):

z ^{( т} ) =

e ² а ( r 1 — r ₀) r 1

∞ ^τ

αn n =1 0

z ( £ ) e ^X n ^{( T 5} ) d^—

ear0 f (0) X^ 1 — e XnT r 1(r 1 — r0) n=    АП

τ

O^ ff ( e£ ) e^-Xn ^{( T-5} ) d£—

( r 1 - r 0 )

∞ ra X An (i n=1 n

e^-X П ^т ) .

(3 . 10)

Так как в силу (3.5) |an| 6 2( т ₀ + т 1), то

^{e 2 а (} т 1 ^— т о ) X    Z

----r-----2n^an I ^{z ( £} ) ^e n =1     ₀

^X П ^{( т-5} ) d£ 6

6 e ² а ( r 1 — r о )( r о + r 1 )

r 1

∞τ kzk         e n=10

^X n ^{( т-5} ) d£ 6

6 e ² C^z^,

Отсюда, следует, что интегральное уравнение (3.10) при 0 < e 6 e ₀ имеет единственное решение z ( т,e ). npi 1чем || z^ < C 1 e. Аналогичное утверждение верно и для уравнения (3.9). Следовательно ||z ° | 6 C ₂ e ².

Из формул (1.10), (2.11), (3.1) и результата, и. 3 следует утверждение основной теоремы и. 1.