О решении плоской задачи теории упругости в декартовых координатах при заданных перемещениях

Заданы как непрерывные функции координат хну перемещения и = и(х, у), и = о(а, у). Тем самым определены деформации

Модуль упругости Е = Е(х,у^ рассматривается как функция координат. Коэффициент Пуассона принят одинаковым во всех точках.

Напряжения выражаются формулами

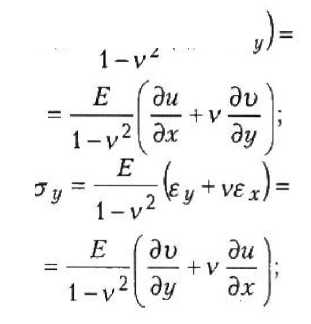
ди ди ди ди

_fl-v^ E тХУ 2    1    2 ^ xy "

E - v Ydu Эм '

-------- —_ -f--, i-v2l 2 i эх d^J

a)

Должны удовлетворяться дифференциальные уравнения равновесия

Э<Тг ₊ ^1^. = О' A^CL + '—L = о Эх Зу ’ Эх Зу

Подстановка в них выражений (1) после некоторых преобразований приводит к следующей системе дифференциальных уравнений с частными производными:

ЗЕ ЗЕ

Эх+/22Э1Г'23

Здесь использованы обозначения

Зи Эи

— +v —;

Эх Зу

V Эи Зи Дох Зу J

Зи

=  +V -—

22 Эх Зу z 1 - v Y Э2м k 2 I Зхду

( дУ

Эх2 >

Решение системы уравнений (2) относительно частных производных выражается формулами

™ = £Fi(x,y);        (4)

Эх

^ = ЕЕ₂^,у\       (5)

Зу

Здесь приняты обозначения е,ы=^УД «>

/ Ц/22 М2/21

F^-^,"^^' <7>

/ и/ 22 ~/ 12/21

Согласно равенству (4)

dl- = Ех(х,у') d^-

Интегрируя, находим:

ln£(x,y) = Ф^х.у^+Ф^    <⁸>

В соответствии с уравнением (5)

^- = F2W)dy.

Е

Интегрирование дает

1н£(х,#)= ф(х,у)+^(х).    (9)

В формулах (8) и (9)

ф(^, у) = J Fi fc У) dx = JF₂ (^, у) dy. (10) Сопоставление равенств (8) и (9) показывает, что <р(у) = у(х) = С. Следовательно In Е(х, у) = Ф(х, г/) + С. Отсюда

Е^Д=С1еФ(1'4    <10

где С_х=е^с.

В качестве С) можно принять модуль упругости £0, относящийся к какой-либо точке тела, например к началу координат. Тогда из уравнения (И) получаем:

EW) ₌ ^_X1y\     (12)

Ео или

^^^ = ехрф(х,у) (13) Ео

Формулы (12) и (13) определяют характер зависимости модуля упругости от координат, при котором обеспечивается удовлетворение дифференциальных уравнений равновесия.

Поскольку согласно соотношению (13) Е = Е^х, у} = Eq exp ф(х, у), формулы напряжений (1) принимают вид сгх _ ехрф(х,у)' Эи    ди'

Eq 1-v² [^{Эх   ду} >

Оу _ ехрф(х, у) ди ₊ Эц £о 1-v² (ду дх _;

т_Ху ехрф(х,у)^1-v ’ ди ди ' Eq 1-v² <2 /Л ду ₍

Соответственно этому выявляются статические условия на поверхности.

Поступила 30.09.04.

ВЛИЯНИЕ РЕГИОНАЛЬНЫХ УСЛОВИЙ ЭКСПЛУАТАЦИИ НА ФОРМИРОВАНИЕ СТРУКТУРЫ И СОДЕРЖАНИЕ СИСТЕМЫ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ И РЕМОНТА МАШИН

Интенсивность изменения параметров технического состояния автомобилей во многом определяется внешними условиями их работы, которые отражаются на надежности транспортных средств, а следовательно, и на эффективности их технической эксплуатации. Они оказывают влияние на режим работы агрегатов, узлов, деталей, ускоряя или замедляя изменение названных показателей [2]. Поэтому учет указанного фактора обязателен в следующих случаях: при расчете требуемых ресурсов (численность персонала, производственная база, запасные части) для обеспечения заданного объема перевозок, что достигается корректированием нормативов; при проектировании автомобилей; при объективном сравнении деятельности автотранспортных предприятий (АТП). От условий эксплуатации зависят не только непосредственные затраты, связанные с техническим обслуживанием (ТО), ремонтом (ТР) или перевозочным процессом в целом, по и сопутствующие.

Обычно различают условия дорожные, движения, транспортные (перевозок), природно-климатические и сезонные, коррозионную агрессивность окружающей среды.

Дорожные условия характеризуются технической категорией дороги (их пять), которые различаются: шириной проезжей части, типом покрытия (П), подъемами и спусками (г), радиусами закругления. Как следует из табл. 1, тип покрытия дороги заметно воздействует на режимы работы автомобиля и его элементов. В свою очередь и последние влияют на них, причем наблюдается определенная связь между режимами работы агрегатов и наработкой па отказ и неисправность (х). Износ и разрушение дорожного покрытия, по данным ИКТП, сокращают надежность автомобиля на 14 — 33 %.

Условия движения отражают воздействие внешних факторов па режимы движения, а потому и на режимы работы, надежность автомобиля и его элементов, себестоимость перевозок. Например, при