О решении проблемы адекватности моделирования в нечеткой логике

Одним из ограничений практического применения нечеткой логики при решении слабоструктурированных задач является проблема точности получаемого решения. При использовании нечеткой логики эксперт предметной области, создавая модель слабоструктурированной задачи, неизбежно искажает существующие зависимости между параметрами задачи, когда указывает продукционные правила и определяет лингвистические переменные и их термы. Созданная таким образом модель может приводить к практически неприемлемым результатам в некоторых областях пространства входных переменных (критических областях).

В связи с этим возникает необходимость коррекции построенной модели. Для эксперта задача модификации созданной им модели, требующая изменения решения в найденных критических областях, является нетривиальной задачей. Использование существующих алгоритмов модификации нечеткой модели [2,3], применение гибридного подхода с использованием нейронных сетей при модификации характеристических функций термов [4] приводят к потере семантики термов и переменных, вводимых экспертом. Также осуществляющиеся изменения носят глобальный характер, что обусловливает появление новых критических областей.

Рассмотрим модификацию алгоритма нечеткого вывода решения Суджено [4], позволяющую осуществлять локальную коррекцию решения в заданном наборе контрольных точек пространства входных данных на примере задачи автоматического управления скоростным колесным роботом.

Задача управления заключается в выборе максимальной скорости прохождения поворота траектории движения, не приводящей к заносу. Упрощая физические условия прохождения виража роботом, будем рассматривать корпус робота как материальную точку и пола- гать, что при прохождении поворота радиусом R в горизонтальной плоскости на него действуют сила тяги двигателя Fдвиж , обеспечивающая линейную скорость движения V , центробежная сила Fц.б. и сила трения Fтр , удерживающая робота от заноса. Тогда для безопасного прохождения виража скорость движения должна удовлетворять соотношению V ≤ kRg (см. Рис.1). Это соотношение будем использовать для оценки адекватности моделирования задачи с использованием нечеткой логики.

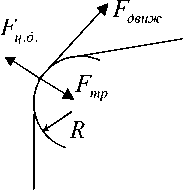
Безопасное прохождение поворота

F _йц.б.        тр.

mV ²

F _{ц . б .} =           F _{тр .} = kmg

R

V ≤ kRg

Рис. 1. Условие безопасного прохождения поворота

Рассмотрим основное содержание модифицированного алгоритма нечеткого вывода. Основная задача модификации – добиться линейной аппроксимации искомой закономерности между входными параметрами задачи в окрестностях контрольных точек, где значение выходного параметра задано. На Рис. 2 изображена плоскость AMN , построенная по контрольным точкам A , B , C и являющаяся линейной аппроксимацией поверхности отклика для выводимой переменной Z , зависящей от переменных X и Y . Множество решений x ^r , определяемых в окрестности точек A , B , C, таких, что x ^r = α ⋅ a ^r + β ⋅ b , α , β ∈ R , задает Зону решений Ψ .

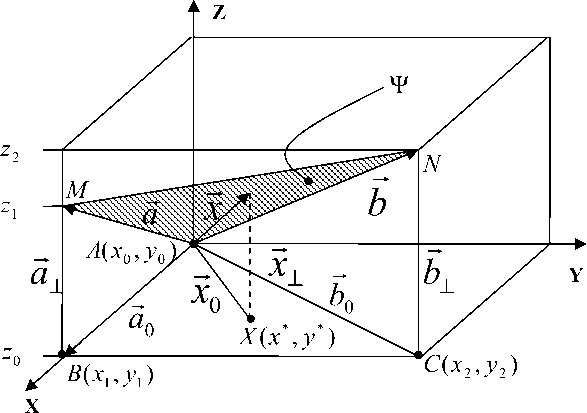
Рис. 2. Линейная оболочка корректирующих данных для точек A, B, C

Можно заметить, что значение zвых выводимой переменной Z, принадлежащее Ψ , при попадании входных данных X(x*, y*) в область определения Зоны Ψ может быть получено из выражения zвых =z0+(g11a⊥+g21b⊥)x*+(g12a⊥+g22b⊥)y*,                       (1)

- 1

где g_ij – коэффициенты матрицы G =

a 0 x b 0 x

V a 0 y b 0 У >  .

Критерий попадания точки X ( x ^*, y ^*) в область определения Зоны Ψ задается соотношением ( α + β ) ∈ [0, 1] и α , β ≥ 0 , а коэффициенты α , β удовлетворяют соотношению α ⋅ a ^r + β ⋅ b = x ^r .

Значение суммы коэффициентов разложения α и β определяется из выражения α + β = ( g ₁₁ + g ₂₁) x ^* + ( g ₁₂ + g ₂₂) y ^* .                            (2)

Модифицируем этап логического вывода Суджено [4] при поиске решения соответствующего продукционному правилу, которое затем будет участвовать на этапе композиции. Для получения результата этапа логического вывода, применяемого к каждому продукционному правилу, в консеквенте которого указана переменная Z, установим соотношение z = z0+αxυx→z +αyυy→z,                         (3)

где α _x = X ₁( x ^*) , α _y = Y ₁( y ^*) – значения степеней истинности для каждого терма левой части правила при некоторых входных данных ( x ^*, y ^*) , υ _{x → z} , υ _{y → z} - коэффициенты влияния переменных X и Y на переменную Z соответственно.

При составлении нечеткой модели эксперт принимает устанавливает переменные υ _x , υ _y равными 0. Таким образом, нечеткий вывод решения осуществляется по упрощенной схеме [4]. Для обеспечения коррекции решения при появлении контрольных точек формируются Зоны решения, построенные на n -симплексах пространства входных данных.

При формировании новой Зоны решения необходимо дополнить набор продукционных правил следующими двумя правилами вида

ЕСЛИ(ОбластьХ = ОбластьХ _ Ψ ) И (Область Y = Область Y _ Ψ )

ТО (Зона = Зона _ Ψ );

ЕСЛИ(Зона = Ψ ) И (ПоправкаХ = Поправка X _ Ψ ) И

(Поправка Y = Поправка Y _ Ψ ) ТО ( Z = Корректировка Z _ Ψ ).

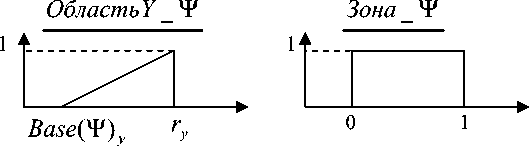
Правило (4) предназначено для определения факта попадания точки с исходными данными X ( x ^*, y ^*) в область определения зоны Ψ . Характеристические функции для термов ОбластьХ _ Ψ , Область Y _ Ψ , Зона_ Ψ определяются как показано на рис. 3.

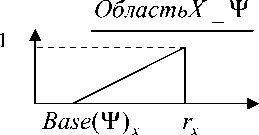
ν x → Зона Ψ = ( g 11 + g 21 )( r x - Base ( Ψ ) x ) ν y → Зона Ψ = ( g 12 + g 22 )( r y - Base ( Ψ ) y )

Зона _ Ψ

14 ___________

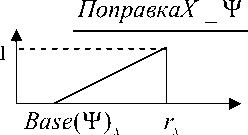
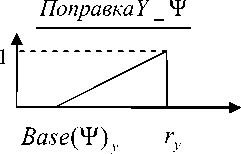
ν _{Зона → Z} = Base ( Ψ ) _z

ν _{x → z} = ( g ₁₁ a _⊥ + g ₂₁ b _⊥ )( r_x - Base ( Ψ ) _x ) ν _{y → z} = ( g ₁₂ a _⊥+ g ₂₂ b _⊥ )( r_y - Base ( Ψ ) _y )

Рис. 3. Определение дополнительных термов поправки выводимой переменной и их коэффициентов влияния

Base ( Ψ ) _x и Base ( Ψ ) _y – координаты x и y основания зоны. r_x и r_y определяют максимальную x и y координату точки корректировочных данных, с помощью которых построена Зона Ψ , при условии, что она не совпадает с координатой основания зоны. Согласно (2) при указанном определении коэффициентов влияния ν _{x → Зона Ψ} и ν _{y → Зона Ψ} каждая точка входных данных X ( x ^*, y ^*) , попадая в область определения Зоны ψ , устанавливает переменную «Зона» в значение «Зона_ ψ », обеспечивая участие правила вида (5) при вычислении поправки выводимой переменной Z .

Правило вида (5) используется непосредственно для вычисления значения выводимой переменной. Вычисление величины поправки по формуле (3) обеспечивает получение решения, принадлежащего Зоне Ψ , при определении коэффициентов влияния ν _{Зона → Z} , ν _{X → Z} , ν _{Y → Z} , указанном на рис. 3.

Рассмотрим решение поставленной задачи автоматического управления скоростью робота при прохождении виража траектории движения. Сформируем следующие правила вывода:

ЕСЛИ (ТРЕНИЕ= “Малое”) И (ПОВОРОТ= “Крутой”), ТО (СКОРОСТЬ = 7)

ЕСЛИ (ТРЕНИЕ= “Высокое ”) И (ПОВОРОТ= “Плавный”), ТО (СКОРОСТЬ = 20).

Определение термов введенных переменных показано на Рис.4.

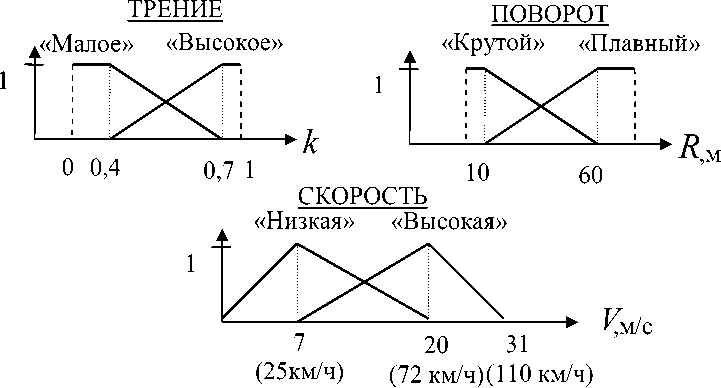
Рис. 4. Термы лингвистических переменных задачи

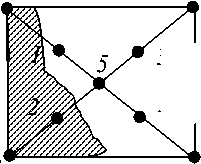
Для проверки адекватности составленной модели рассмотрим область пространства входных данных Ω = k × R = [0.4; 0.7] × [10; 60] , изображенную в виде прямоугольной области на рис. 5.

Применение упрощенного подхода при нечетком выводе показывает, что в точках A , C и 2 решение превосходит максимально допустимое значение скорости, рассчитанное по аналитической формуле. Это означает, что в окрестностях этих точек составленная модель не адекватна и получаемые решения практически не приемлемы, так как приводят к заносу робота.

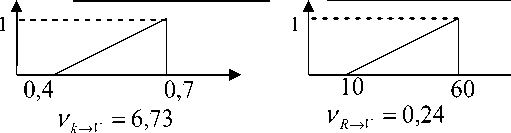
Для коррекции решения в окрестностях точек A , C и 2 построим Зону решений на основе контрольных точек A , B и С. Определения поправочных термов и значения коэффициентов влияния ν _{Зона → V} , ν _{k → V} , ν _{R → V} входных переменных на выводимую переменную «Скорость» даны на рис. 5.

Можно заметить, что решение в окрестностях проблемных точек стало практически приемлемым, поскольку скорость не превышает максимально допустимых значений, приводящих к заносу.

Зона _ ABC

V Зона^У   1 1

Поправкаk _ ABC

ПоправкаR _ ABC

Точка	k	R	V max = gkRR	Упрощенный нечеткий вывод	Модификация нечеткого вывода
A	0,41	11,0	6,65	7,26	6,57
B	0,69	59,0	19,97	19,74	19,97
C	0,69	11,0	8,62	11,88	8,45
1	0,5	25,0	11,07	11,03	10,54
2	0,6	25,0	12,12	13,16	11,21
4	0,6	45,0	16,27	15,98	16,0
5	0,55	35,0	13,73	13,50	13,27

0,4

0,7

60 R

A

D

B

k

Рис. 5. Сводная таблица результатов моделирования для зоны в окрестности ABC

Таким образом, рассмотренная модификация нечеткого вывода позволяет снизить влияние субъективного фактора, ухудшающего качество решения из-за неточностей, вносимых экспертом при описании некоторой системы. На практике в задачах управления и распознавания в областях исходных данных, где существует неполная осведомленность о закономерностях работы системы, альтернативные механизмы нечеткого вывода приводят к ошибочным решениям, превышающим заданный порог точности решения. Рассмотренный подход позволяет получить желаемое решение в требуемой области пространства исходных данных, включая те области, где знания эксперта, выраженные в нечетком описании системы, оказываются неточными или ошибочными, что достигается с помощью набора корректировочных данных, задающих требуемые значения решения. При этом корректировочные данные приводят не к модификации созданных экспертом правил или определений характеристических функций, а к дополнению существующего описания, что позволяет сохранить объяснительную возможность нечеткого вывода решения в терминах, введенных экспертом.