О решении задачи оптимального выбора параметров питания линейной индукционной машины генетическим алгоритмом с локальным поиском

Постановка задачи оптимизации структуры ЛИМ. Линейные индукционные машины (ЛИМ) с повышенным рабочим зазором широко используются в металлургии с целью повышения производительности и энергетической эффективности плавильно-литейных агрегатов. Увеличение рабочего зазора обусловлено необходимостью расположения теплоизоляции между индуктором и рабочим телом (расплавом металла). Наличие в ЛИМ значительного немагнитного зазора определяет особенности их конструкции и режимы работы. В частности, для эффективной работы ЛИМ существенными становятся продольный и поперечный краевые эффекты, которые значительно усложняют расчеты при проектировании и моделировании функционирования ЛИМ классическими методами. Следовательно, возникает необходимость в применении численного имитационного математического моделирования с использованием коммерческих пакетов, которые позволяют учитывать краевые эффекты при изучении процессов, происходящих в ЛИМ [1].

Линейные индукционные машины металлургического назначения предназначены для бесконтактного силового воздействия на расплавы металлов в печах и миксерах с целью их перемешивания, дозирования и транспортировки (рис. 1). Индуктор ЛИМ состоит из ферромагнитного сердечника, собранного из листов электротехнической стали, и многофазной обмотки, расположен- ной в пазах сердечника. Обычно применяют трехфазные обмотки, аналогичные обмоткам нормальных асинхронных машин.

Рис. 1. Общий вид плоской ЛИМ

При питании плоской ЛИМ переменным током в зазоре между сердечником и рабочим телом возникает бегущее магнитное поле, подобное вращающемуся полю асинхронной электрической машины. Это магнитное поле индуктирует в металле токи, что приводит к возникновению электромагнитных сил, под действием которых развивается усилие и металл приходит в движение [1].

К качеству работы ЛИМ предъявляются строгие требования как с точки зрения технологической и энергетической эффективности, так и с точки зрения надежности. Приоритеты и характер этих требований меняются в зависимости от способа использования машины. К примеру, ЛИМ для дозирования и транспортировки жидких металлов должны обеспечивать строгое линейное движение, так как перпендикулярное движение создает дополнительные гидравлические сопротивления, а это приводит к снижению эффективности работы ЛИМ в составе плавильно-литейного агрегата и дополнительным энергетическим затратам [1]. Совершенно иные требования предъявляются при использовании ЛИМ в качестве пе-ремешивателя металла или кристаллизатора. Главная задача при этом сводится к эффективному растворению легирующих добавок по всему объему ванны печи. В этом случае необходимо создавать движения как в вертикальной, так и в горизонтальной плоскости ванны с металлом, но при этом восходящие потоки не должны разрывать оксидную пленку на поверхности.

Итак, обобщая все требования, можно выделить критерий, который характеризует эффективную работу ЛИМ, – это усилие F (сила Лоренца), развиваемое в жидком металле. Усилие F – векторная величина, а это значит, что его можно разложить на три орта: F_x – составляющую, создающую линейное движение; F_y – составляющую, которая смещает ось движения металла (основываясь на трудах А. И. Вольдека, можно считать, что данная составляющая стремится к нулю); F_z – составляющую, создающую восходящие гидродинамические потоки металла. Таким образом, для определения остаются только два критерия. В данной статье рассматриваются вопросы максимизации составляющей F_x , так как она важна во всех случаях применения ЛИМ в металлургии.

Электромагнитное поле в расчетной области описывается системой уравнений Максвелла:

rotH=γ(E+[V×B]),(1)

rotE =-∂B ,

∂t divB =0,(3)

B=µ0µrH, где H – напряженность магнитного поля, А/м; E – напряженность электрического поля, В/м; V – скорость, м/с; t – время, с; µ0 – магнитная постоянная, Гн/м; µr – абсолютная магнитная проницаемость [2].

Решение системы уравнений электромагнитного поля осуществлялется относительно векторного магнитного потенциала:

∆ A - µ ₀ µ _r γ ^{∂ A} + µ ₀ µ _r γ [ V rot A ] = 0,          (5)

∂t где A – векторный магнитный потенциал, В ⋅ с/м; γ – удельная электрическая проводимость; V – вектор скорости движения элементарного объема жидкого металла.

В результате решения данного уравнения можно найти все характеристики электромагнитного поля, в том числе и искомую силу Лоренца:

F = ∫ N ^T ( J _t × B ) d ( vol ),               (6)

vol где N – вектор функции формы; Jt – вектор полной плотности тока; B – вектор магнитной индукции [3].

Целевую функцию задачи оптимизации обозначим W ( X ), где X = ( I ₁, I ₂, I ₃, ϕ ₁, ϕ ₁, ϕ ₃, f ). С целью классической постановки задачи оптимизации ее нужно привести к задаче минимизации целевой функции:

W ( X )= ¹ →min. (7) 1+ F x ²( Х ) X

В формуле (7) величина F_x при фиксированных параметрах ЛИМ рассчитывается с помощью модели ЛИМ, разработанной в пакете математического моделирования ANSYS.

Рассмотрим, что представляет собой вектор параметров Х . Характер поведения усилий и их значения зависят от многих факторов: токов, сдвигов фаз, частоты питающего напряжения, типа конструкции ЛИМ, ширины активной части магнитопровода и т. д. Решающими параметрами при сохранении геометрии машины являются параметры питания (токи I ₁, I ₂, I ₃, фазы токов в катушках ϕ ₁, ϕ ₂, ϕ ₃, частота питающего напряжения f ), варьирование которых вызывает различные эффекты в жидком металле (например, увеличение составляющей F_x приводит к возникновению ламинарного движения в металле вместо турбулентного, уменьшению эффекта отталкивания и т. д.). Для исследуемой модели ЛИМ следует учитывать, что все параметры вектора Х изменяются дискретно, а принятые ограничения данных параметров обусловлены как конструкцией машины, так и возможностью серийно выпускаемых источников питания [3]:

– пределы изменения токов I ₁, I ₂, I ₃ в проводниках катушек приняты от 15 до 25 с шагом дискретизации, равным 0,5, при этом проверяется гипотеза, что для достижения максимума F_x необходимо наличие асимметрии токов в катушках (верхний предел выбран исходя из максимальной термической стойкости изоляции обмоток ЛИМ);

– фазы токов рассматриваются только во второй ϕ ₂ и третьей ϕ ₃ катушках в диапазоне от 1 до 360 электрических градусов с шагом 1 градус, а фаза в первой катушке ϕ ₁ приравнивается к 0;

– частота питающего напряжения f задается в диапазоне от 1 до 60 Гц (диапазон выбран исходя из возможностей источника питания и накопленного инженерного опыта) с шагом дискретизации, равным 1.

Решение задачи оптимизации. Постановка задачи оптимизации (7) характеризуется алгоритмически (инструментально, с помощью модели) рассчитываемой целевой функцией с дискретными переменными. Подобная постановка требует соответствующего выбора алгоритма оптимизации. Стохастические оптимизационные алгоритмы давно зарекомендовали себя как эффективное и удобное средство решения практических задач оптимизации [2].

В настоящее время большую популярность благодаря простоте реализации и эффективности приобрел класс методов под общим названием «эволюционные алгоритмы» [4]. Ярким примером таких алгоритмов оптимизации является генетический алгоритм (ГА), каждое решение которого представляется в виде бинарной строки, называемой хромосомой. Множество решений ГА называют популяцией. Поисковые операторы этого алгоритма имитируют процессы селекции, скрещивания, мутации, происходящие в живой природе.

Как показывает практика применения эволюционных алгоритмов, высокая размерность задач, нелинейность и многоэкстремальность целевой функции не создают для них дополнительных трудностей.

Пошаговая структура генетического алгоритма выглядит следующим образом:

• 1)    инициализация популяции. Создается массив индивидов

Population = Initialization( X ), где Population = { x 1 , x 1 ,..., x_N } , xi e X , i = 1, N ;

• 2)    вычисление функции пригодности для индивидов. Создается массив:

Fitness = { f ( X i ),..., f ( Xn ) } , i = 1, N ;

• 3)    запоминание лучшего индивида и значения его целевой функции:

Best = arg max f ( x );

x e Population

• 4)    повтор выполнения операторов селекции, рекомбинации и мутации ( M – 1) раз и переход к шагу 1.

Размер популяции N , число поколений M и типы операторов являются параметрами (установками) генетического алгоритма, варьирование которых позволяет получить разные по эффективности реализации ГА. Существуют несколько реализаций для каждого из генетических операторов.

В бинарном ГА генотип (решение) представляет собой бинарный вектор, полученный из вещественного или целочисленного вектора фиксированной длины Length:

^X = ⁽ ^ i ,-, ^X Length ), ^X i ^{e R} или ^Z ■

Каждая координата может изменяться в некотором заданном интервале с выбранным шагом дискретизации, множество которых определяет область поиска в соответствующем пространстве поиска.

Одним из главных недостатков генетического алгоритма является сходимость к глобальному решению лишь по вероятности. Другими словами, процесс оптимизации этого алгоритма может остановиться в некоторой точке, которая не будет оптимумом. Для устранения данного недостатка используют подходящий алгоритм локального поиска для уточнения решения, найденного генетическим алгоритмом, параметры которого представлены в табл. 1.

Анализ табл. 1 показывает, что область поиска задана на дискретной решетке (гиперкубе), размерность которой равна порядка 1010 точек.

В данной работе в качестве алгоритма локального поиска использовался целочисленный алгоритм локальной оптимизации с переходом по первому улучшению.

Выбранные алгоритмы и подход к оптимизации были реализованы с использованием разработанной программной системы на языке высокого уровня C++ Builder 6.0 (окно настроек области поиска и генетического алгоритма и подключения внешней целевой функции этой системы представлено на рис. 2).

Оптимизация проводилась генетическим алгоритмом со следующими настройками: турнирная селекция (размер турнира равен 3), равномерное скрещивание, средняя мутация. Настройки генетического алгоритма выбраны как наиболее универсальные для неизвестной оптимизируемой функции. Число вычислений целевой функции в ГА равно 4 900 (70 индивидов на 70 поколений). Расчет одного значения целевой функции занимает порядка 5 мин. Таким образом, на расчет отводилось почти 17 сут непрерывной работы программы. Оптимизация была прервана на 30 поколении из-за того, что улучшения в оптимизации не наступало (стагнация). Найденное на тот момент решение было хуже уже известного решения. Полученное генетическим алгоритмом решение было уточнено локальным поиском (табл. 2). Параллельно с работой генетического алгоритма была запушена программа оптимизации локальным поиском с целью улучшения известного решения. В результате улучшенное локальным поиском решение без использования генетического алгоритма и решение с использованием ГА совпали.

Результаты оптимизации позволили сделать следующие выводы:

• –    генетический алгоритм не нашел решения лучше известного в связи с тем, что известное решение было достаточно близким к улучшенному решению, т. е. четыре из шести варьируемых параметров были определены точно лучшими и в улучшении уже не нуждались;

• –    локальный поиск, стартовавший из известного решения и решения, найденного генетическим алгоритмом, завершился в одной и той же точке области поиска, тем самым было найден локальный минимум, который, возможно, является глобальным минимумом;

• –    результат оптимизации позволил сформулировать гипотезу о том, что оптимизируемая целевая функция является монотонной и унимодальной.

С целью проверки гипотезы о наличии свойств монотонности и унимодальности целевой функции локальный поиск был осуществлен из нескольких крайних (гранич-

Таблица 1

Параметры структуры области поиска

Наименование параметра (независимой переменной) оптимизации Обозначение в программной системе Диапазон (левая граница) Диапазон (правая граница) Дискретизация (шаг сетки) Сила тока в первой катушке, А I1 15 25 0,5 Сила тока во второй катушке, А I2 15 25 0,5 Сила тока в третьей катушке, А I3 15 25 0,5 Фаза во второй катушке, град fi2 1 180 1 Фаза в третьей катушке, град fi3 1 180 1 Частота питающего напряжения, Гц f 20 80 1 ных) точек пространства поиска (рис. 3). Гипотеза под- совпали с решением, найденным ранее и отображенным твердилась: найденные решения были одинаковыми и в табл. 2.

Рис. 2. Основные рабочие окна программной системы

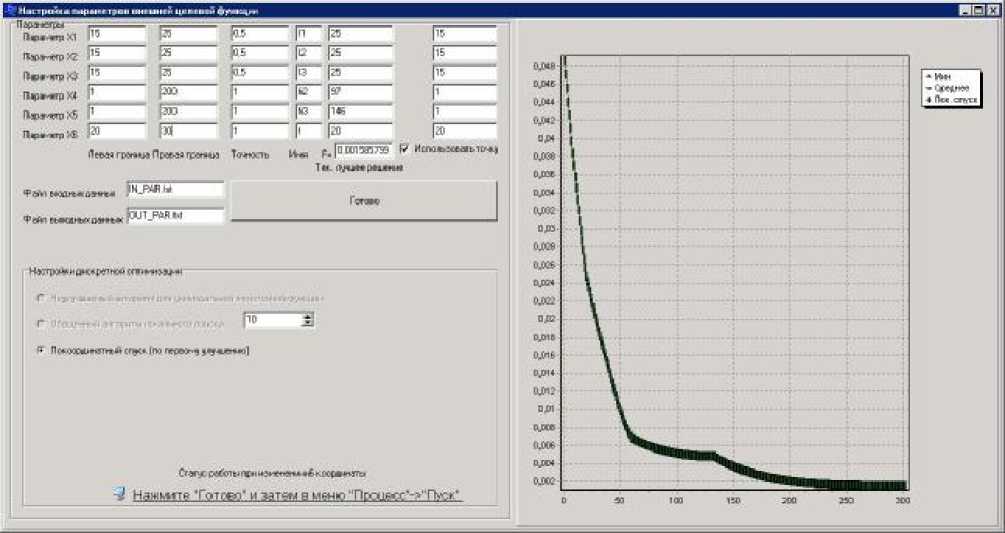
Рис. 3. График сходимости локального поиска из крайней точки в точку локального (глобального) минимума