О решении задачи равновесия мягкой сетчатой оболочки при наличии нагрузки, сосредоточенной в точке

В работе рассматривается пространственная задача о равновесном состоянии мягкой сетчатой оболочки при наличии внешней точечной нагрузки, сосредоточенной в некоторой точке. Под сетчатой понимается оболочка, силовой основой которой является сетка, образованная двумя семействами взаимно перекрещивающихся, абсолютно гибких, упругих нитей. Предполагается, что функции, описывающие физические соотношения в нитях, являются непрерывными, неубывающими и имеют линейный рост на бесконечности. Решаемые здесь задачи весьма часто возникают в механике, медицине, при проектиро- вании различного рода конструкций, изготовленных из тканевых или пленочных материалов (см., например, [1-13]).

Задачи об определении положения равновесия мягкой сетчатой оболочки рассматривались и ранее (см., например, [14-18]). При этом обобщенные задачи формулировались в виде уравнений или вариаци- онных неравенств с оператором, действующим в случае линейного роста функций, описывающих физические соотношения в нитях, из соболевского пространства V =

o

W 1

в сопряженное с ним, и соответ-

ственно рассматривается ситуация, когда функция, описывающая плотность внешних источников, определяет линейный непрерывный функционал на V .

В настоящей работе проводится исследование задач теории мягких сетчатых оболочек с менее гладкой правой частью: каждый точечный источник, в неодномерном случае моделируется дельта-функцией

Дирака, которая не принадлежит пространству, сопряженному с V .

Обойти указанную выше трудность удалось благодаря аддитивному выделению особенности, связанной с дельта-функцией.

Обобщенная постановка задачи сформулирована в виде инте- грального тождества относительно функции

' °, 13

W 1

.

Затем введена

вспомогательная задача с правой частью, задаваемой дельта-функцией. Для вспомогательной задачи известно решение в явном виде. Благодаря этому обобщенная постановка свелась к нахождению решения операторного уравнения в V. Установлены свойства оператора, входящего в это уравнение - ограниченность, непрерывность, монотонность, ко- эрцитивность, что дало возможность применить для доказательства теоремы существования известные результаты теории монотонных операторов (см., например, [19, 20]). Доказано, что множество решений обобщенной задачи не пусто, выпукло и замкнуто. Вообще говоря, решение обобщенной задачи не единственно. Однако установлено, что усилия в нитях определяются однозначно.

Отметим, что аналогичный подход был использован при рассмотрении стационарных задач фильтрации несжимаемой жидкости, следующей закону фильтрации с предельным градиентом, при наличии точечного источника [21, 22].

Построены конечномерные аппроксимации задачи, исследована их сходимость. Для решения задач использован разработанный в работе [23] двухслойный итерационный метод. Данный метод был реализован численно. Проведенные для модельных задач численные эксперименты подтвердили эффективность итерационного метода.

1.    Постановка задачи

Рассмотрим пространственную задачу о равновесном состоянии мягкой сетчатой оболочки при наличии точечной нагрузки. Под сетчатой понимается оболочка, силовой основой которой является сетка, образованная двумя семействами взаимно перекрещивающихся, абсолютно гибких, упругих нитей. Предполагается, что узлы сети фиксированы, материал, заполняющий промежутки между нитями, не сопротивляется деформации, и ни в начальном состоянии, ни в процессе деформации соседние нити не соприкасаются. Ячейки сети считаются малыми и не сопротивляющимися сдвиговым деформациям. Деформации и перемещения допускаются конечными.

Введем в пространстве декартову систему координат ( x 1 ,x ₂, x 3 ). Считаем, что в недеформированном состоянии оболочка может быть описана поверхностью ^ ( а ) = (^( а ),^,₂( а ), ^ ₃( а )), где а = ( а 1 , а ₂) еП -лагранжевы координаты; П - ограниченная область из R ² с непрерывной по Липшицу границей Г . Предполагаем, что функция ^ удовлетворяет условиям: i<^ C 1 ( Q ) J , для любого аеП справедливо неравенство |[д 1 ^ ( а ), д ₂ ^ ( а ) ]|> c >  0 .

Лагранжевы координаты ( a , , a ₂) выберем так, что координатные линии сонаправлены с нитями, образующими оболочку.

Через w ( а ) = ( w j ( a ), w ₂( a ), w 3 ( a )) обозначим функцию, описывающую поверхность оболочки в деформированном состоянии, через G ( a ) =|[ d ₁ w ( a ), d ₂ w ( а ) ]| ² - дискриминант метрического тензора поверхности деформированной оболочки.

Здесь использованы обозначения: d j = д / da j , j = 1,2 ; [ • , • ] , ( • , • ) и | • | - векторное, скалярное произведения и норма в R ³ соответственно.

Введем также следующие обозначения (для j = 1,2): j* = 3 - j; rj =d jw - вектора, образующие ковариантный локальный базис на деформированной поверхности; gj =| d j£|, Gj =| djw| - параметры Ляме соответственно недеформированной и деформированной поверхности оболочки; r 1,r2- векторы, образующие контрвариантный локальный базис на деформированной поверхности: (rj.,rm) = 5 jm .

Обозначим через Fj внутреннюю силу, действующую на единицу длины aj -й координатной линии (aj = const) деформированной оболочки с той стороны оболочки, куда направлен вектор rj , j = 1,2, через F,m - коэффициенты разложения этой плотности сил по еди-

2 Fi"

ничным векторам локального базиса:

FJ =У —— rm . Тогда ковари-m=1 m антные компоненты тензора

напряжений T = ^ T^jmr j r_m j , m = 1

связаны

с погонными усилиями F jm соотношениями GG T ^Jm = F^jmG j . / G m

(см. [24, с. 50]).

Для сетчатой оболочки в силу того, что в выбранной лагранжевой системе координат направления осей совпадают с направлениями нитей, имеем [25]: F12 = F21 = 0 (то есть ячейка сети не оказывает сопротивления повороту нитей в узлах скрепления), Fj = bj(Xj)рjg.. /Gj., где X j = g j / Gj - относительные степени удлинения.

Здесь b 1,b2: R + > R + - функции, характеризующие физические свойства нитей; р j : Q > R + - количество нитей, сонаправленных с aj -й координатной осью, на единицу длины aj -й координатной оси в недеформированном состоянии. Эти функции определены конструкцией сетчатой оболочки, и относительно них считаем выполненными условия bj е С (R +), bj (X) > bj (Z) при X>Z> 1, bj (Z) = 0 при Z< 1 ,(2)

существуют постоянные c0,c1,k > 0, такие, что рj е C(Q), р j (a) > с0 для всех aeQ, kZ- C1 < bj (Z) < kZ.(3)

Заметим, что, вообще говоря, направления r j не являются главными для тензора T , хотя смешанные компоненты T^jm и равны нулю.

Уравнение равновесия оболочки, находящейся под воздействием внешних сил, в декартовой системе координат имеет следующий вид (см. [24, с. 88]):

2 b (| d w |/ g )

£ «/    ,4 ',   P j g ,* d j w ) + GPp + G Y Y Q = 0,        (4)

j=         |djw|          j где P, Q - векторы плотности соответственно поверхностной и массовой нагрузок; у - плотность материала оболочки в деформированном состоянии.

В силу закона сохранения массы G Y y=| [ d ₁ ^ ( a ), d ₂ ^ ( a ) ]|y , где у : Q >  R ¹ - заданная плотность материала недеформированной оболочки. Будем считать, что плотность материала равна единице ( у = 1 ) и р 1 =р ₂ = 1 . Поверхностная нагрузка предполагается равной нулю:

P = 0. Поэтому в силу того, что [ д ₁ ^ ( а ), 6 ₂ ^ ( а ) ] = 1 , g ₁ = g ₂ = 1 , уравнение (4) примет следующий вид:

2      b, (| 6 w |)

• - j(j)+Q=0.

Далее будем считать края оболочки закрепленными:

w(а1,а2) = ^(а15а2), (а1,а2) еГ.(6)

Вариационная постановка задачи (5), (6) в перемещениях состоит в нахождении вектор-функции v = w - £ , такой, что

4, r bj(|dj( v + !;Щ ,„

П( 16 (v < _> 5j(v ":dа- j=1 Q

- J ( Q ( а ), р ( а )) d а = 0 Vpe [ C ° ( Q )]³.

Предполагаем, что массовая нагрузка, действующая на оболочку, сосредоточена во внутренней точке а * множества Q и имеет интенсивность q = ( q ₁, q ₂, q ₃), q j = const , j = 1,2,3 .

Приведем обобщенную формулировку рассматриваемой задачи. o

Определим пространство W ^ ( Q ) как пополнение пространства C 0° ( Q ) по норме ||п|| = ||⁶ 1 П|| _{£ 1}⁺||⁶ 2 П| L₁ .

Под обобщенным решением задачи (7) будем понимать функцию

v е

' °,       13

W /( Q )

такую, что

2     b j (^ j ( v + ^ )_D

:- ^1 q ⁽ ^j ( v +^ )i

⁶ j ⁽ v ⁺ O> ⁶ j n ) d ^а= ⁽ q , п ^{( а} * )) vp ^{е [} C 0 ° ^{( Q )]}

o

Определим пространство W ₂( Q ) как пополнение пространства

С ° ⁽ Q ) по норме ||п|| = ||^д1П|| _L + ||^д2П| L_l , где ||^d j < = ⁽ f | 5 j П ^{( а} )| ² d ^{а )1/2} ,

2                    "*"^2                            "L 2

п

,0

j = 1,2 , и обозначим V = W^( O )

. Рассмотрим вспомогательную за-

дачу поиска функции ф = ( ф ₁₅ ф ₂, ф ₃) такой, что

^- k Аф i = q i 5 ⁽ а^-а ), ае° , _{z х}                            i = ^{1,2,3                  (9)}

ф i (а) = 0, аеГ, где к - постоянная из условия (1), 5 - дельта-функция Дирака.

o

Решение задачи (9) существует, и ф i е W/(O) для каждого i = 1,2,3, (см., например [26, стр. 163]. Поэтому фе

W ?(O)

Вариационная постановка задачи (9) выглядит следующим образом: Найти

фе

W ?(O)

: к Г j ( 6 , .ф( а ), д j п ( а )) d а= ( q , п ( а ’ )) V_ne [ С ° ( П )]³. j = 1 о

Решение задачи (9) будем искать в виде v = и + ф , где и е V - неизвестная функция, а ф - решение задачи (10).

Введем далее операторы Л j : V ^ [ L ₂( П )] ³ , B j : R ³ ^ R ³ , j = 1,2 , по формулам Л j ( и ) = d j ( ^ + и +ф ) , B j ( y ) = b j. (| y |) у /| y | , у ^ 0 , B j (0) = 0 . При этом B j ( Л j U ( а )) , а е П , j = 1,2 , - усилия в нитях.

С учетом введенных обозначений задача (8) сводится к поиску функции и е V , такой, что

2                                     2

Г] (B j ( Л j U ), a j .n) d а= к rj ( d j ф , 8 j n ) d а V_ne [ C 0° ( П )] ³ .    (11)

j = 1 O                           j = 1 о

Справедлива

Теорема 1. Задача (11) имеет непустое, выпуклое, замкнутое множество решений. Если v - решение (8), то v = и + ф , где и - решение задачи (11); ф - решение задачи (10).

Определим на V х V форму a(и,n) = a1(и,р) + а2(и,n) + к(^ + и,n)V , где aj

^{( и} , П ) = J

п

b j ^{(| Л} j u ) ^{| Л} j u |

- к | Л j U |

( Л j U , д j n ) d а , j = 1,2 . Нетрудно про

верить, что форма а непрерывна и линейна по второму аргументу. Поэтому по теореме Рисса-Фишера эта форма порождает оператор A : V ^ V , а ( и , n ) = ( Au , n ) V . Таким образом, обобщенная задача (12)

эквивалентна операторному уравнению

Аи = 0.                            (12)

При выполнении условий, наложенных на функции b j , можно доказать, что оператор А является ограниченным, непрерывным, монотонным и коэрцитивным, поэтому существование решения уравнения (12), выпуклость и замкнутость множества его решений следует из общих результатов теории монотонных операторов (см., например [19, 20]). По аналогии с [21, 22] устанавливается справедливость второго утверждения теоремы 1.

Отметим, что, вообще говоря, решение задачи (12) не единственно. Однако имеет место

Теорема 2. Пусть выполнены условия (1)–(3), кроме того, функции b_j липшиц-непрерывны:

| b j ( У- b j ( Z )| < c ₂| Z — Z |, С 2 >  о, j = 1,2.

Тогда, если u – решение задачи (12), то усилия в нитях B j ( Л j U ( а )) , а еП , j = 1,2 , определяются единственным образом.

Справедливость теоремы устанавливается по аналогии с [27].

3.    Конечномерные аппроксимации задачи

При построении конечномерных аппроксимаций для простоты будем предполагать, что область Qc R ² является многоугольником. Пусть 3 h - некоторое семейство (триангуляция) треугольников K , обладающее свойствами:

• 1)    U K = Q ;

K ∈ ℑ h

• 2)    int K I int K’ 0 V K , K ‘e3 h ;

• 3)    для любых K , K ‘e3 h множество K I K ‘ если не пусто, то является либо стороной, либо вершиной одновременно треугольников K , K' ;

• 4)    триангуляция 3 h является регулярной [28, 29]:

max R K / r_K <  c < -^ , h = max R K I r_K .

K ∈ ℑ _h                  K ∈ ℑ _h

Здесь R K - диаметр наименьшего шара, содержащего K ; r_K - наибольшего шара, содержащегося в наибольшем шаре, содержащего в K .

Определим теперь конечномерные пространства W h и V h , ассоциированные c триангуляцией 3 h :

ooo

W h = X h ^х X h ^х X h , V h = X h ^x X h ^x X h , где X h — пространство непрерывных функций, являющихся на каждом o

K из 3 h полиномами не выше первого порядка; X h — пространство непрерывных функций из X h , равных нулю на границе множества О .

oo

Очевидно, что X h с W /( Q ), X h с W^( Q ) , и, значит, V h с V . При этом (см., например, [30])

Vne V Я { n _h } _h > ₀ с V : n _h >П ^пР^{и h} ^ ⁰-

Задаче (12) сопоставим следующую задачу: Найти uh e Vh: (Auh ,nh)v = 0 Vuhe Vh •                 (14)

Справедливы следующие результаты:

Теорема 3. Пусть выполнены условия (1)–(3). Тогда задача (14) имеет непустое, выпуклое и замкнутое множество решений, множество { U h } h > 0 решений задачи (14) равномерно ограничено по h:

II u h II V ^- c 3 ^V h >  ⁰⁰

где константа c3 > 0 не зависит от h. Если подпоследовательность {uh } ”1 слабо сходится к и * в V при hi ^ 0, то и * - решение i задачи (14).

Так же, как и при доказательстве теоремы 1, используя монотонность, непрерывность и коэрцитивность оператора А , получаем существование непустого, выпуклого и замкнутого множества решений задачи (14). В силу коэрцитивности оператора А множество {Uh}h>о решений задачи (14) равномерно ограничено по h, т.е. справедлива априорная оценка (15). Из этой оценки следует существование подпоследовательности {Uh } ”1, слабо сходящейся к некоторому элементу и * i в V при hi ^ 0 . Используя монотонность и непрерывность, а значит, псевдомонотонность [19] оператора А, получаем стандартным образом (см., например [19, 30]), что и * - решение задачи (14).

Теорема 4. Пусть выполнены условия (1)–(3), (13), решение u

o

задачи (12) принадлежит пространству W22(Q) . Тогда справед- лива оценка

IIи -uhIIv- c*Vh с константой c* , не зависящей от h .

4.    Итерационный метод

В заключение отметим, что при выполнении условий (1)-(3), (13), наложенных на функции b , оператор А является потенциальным, липшиц-непрерывным и обратно сильно монотонным [31, 32]. Поэтому для решения задачи (12) можно использовать следующий итерационный процесс [23]. Пусть и ⁽⁰⁾ - произвольный элемент из V . Для k = 1,2, к определим вектор и ⁽⁰⁾ как решение уравнения

-А ( и ^{( k + 1)} - и ^{( k} ) ) = т Аи ^{( k} ) ,                        (16)

где т >  0 - итерационный параметр.

Теорема 5. Пусть выполнены условия (1)-(3), (13), те (0,2/ c 3 ) .

Тогда итерационная последовательность {u(k)}^=1, построенная со- гласно (16), сходится слабо в V к некоторому решению задачи (12).

Указанный алгоритм решения задачи реализован в виде комплекса программ в среде MATLAB. Программа выполнена в соответствии с модульным принципом, что позволило осуществить раздельное программирование, отладку и тестирование составных частей пакета программ, а также простую модернизацию и настройку пакета на решение задач различного уровня сложности.

Проведенные для модельных задач численные эксперименты подтвердили эффективность итерационного метода. В качестве области Q выбирался квадрат (0,1) х (0,1) , функции b j полагались равными

bj©=

/ 0, ^< 1,

U-1, ^> 1,

внешняя нагрузка была сосредоточена в точке

(0.5,0.5) , интенсивность нагрузки полагалась q = - 0,05. В качестве начального приближения в итерационном методе (16) выбирались функции, соответствующие недеформированной оболочке.

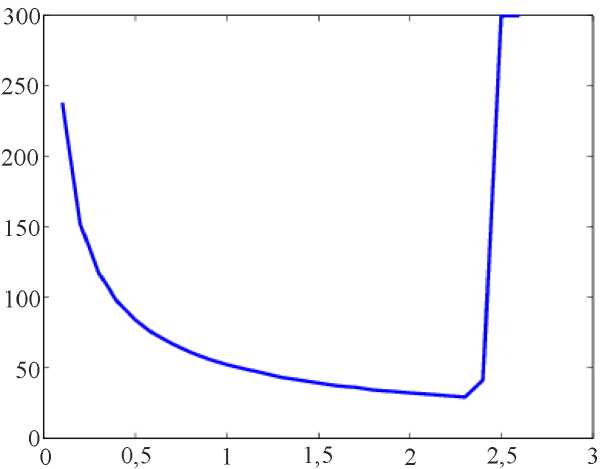
Рис. 1. Зависимость числа итераций от итерационного параметра τ

В результате численных экспериментов было найдено оптимальное (по количеству итераций) значение итерационного параметра (рис. 1). Это значение практически не зависит от числа разбиений (рис. 2). Значение максимального прогиба (в центре квадрата) также не зависит от количества точек сетки (рис. 3). На рис. 4 представлена форма деформированной оболочки.

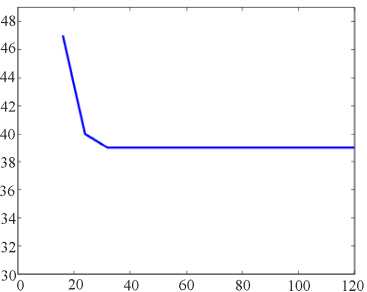
Рис. 2. Зависимость оптимального числа итераций от количества точек сетки

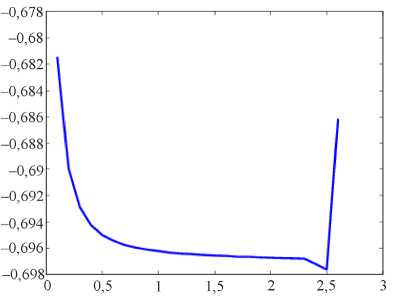
Рис. 3. Зависимость прогиба в центральной точке от итерационного параметра τ

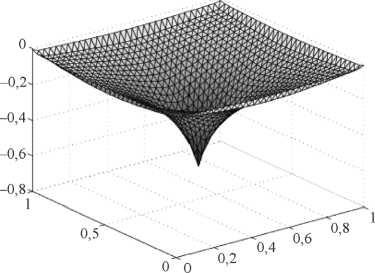
Рис. 4. Форма деформированной оболочки

Работа выполнена при финансовой поддержке РФФИ (проекты 11-01-00864, 12-01-00955, 12-01-97026, 12-01-31515, 13-01-00908).