О синтезе высокооднородного поля постоянного магнита в МР-томографии

В МР-томографии важной задачей является задача формирования (синтеза) высокооднородного магнитного поля в МР-томографе, т. к. только при высокой однородности поля можно получать томограммы с высоким разрешением [1, с. 51–53]. В данной работе рассматриваются постоянные (перманентные) магниты для создания полей [2–6].

Преимущество постоянных магнитов перед сверхпроводящими и резистивными магнитами состоит в том, что постоянные магниты не требуют охлаждения жидким гелием или водой, питания электричеством и являются более дешевыми. Правда, они создают низкие поля — около 0.2 Тл, но это не является недостатком, т. к. в последние годы ведущие фирмы-производители МР-томо-графов (General Electric, Siemens, Toshiba и др.) основное внимание уделяют выпуску среднепольных и даже низкопольных МР-томографов (с полем не выше = 0.5 Тл), поскольку выяснилось, что в большинстве областей применения (кроме МР-спектроскопии) высокопольные томографы (выше = 1.5 Тл) не имеют существенных преимуществ перед средне- и даже низкопольными томографами.

Однако расчет конфигурации постоянного магнита, при которой формируется высокооднородное магнитное поле, требует специального алгоритмического подхода. Дело в следующем. Для различных типов витков с током существуют формулы для расчета их магнитных полей, вытекающие из закона Био—Савара—Лапласа [7, с. 326–335]. А для магнитного поля постоянного магнита нет аналогичного закона и соответствующих формул (заметим, что закон Ампера [7, с. 339] не дает закон и формулу для поля магнита или его элемента).

АНАЛОГИЯ МЕЖДУ МАГНИТОМ И НАБОРОМ ВИТКОВ С ТОКОМ

Чтобы преодолеть отмеченные трудности, в данной работе для разработки удобного математического аппарата, необходимого для определения параметров постоянного магнита и расчета его поля, используется следующая аналогия [7, с. 356].

Рассмотрим магнит в виде однородного цилиндра (рис. 1). Под влиянием внешнего поля H ₀ в толще цилиндра у частиц (протонов) возникает ларморова прецессия их магнитных моментов [1, с. 34–36], причем у парамагнетиков и ферромагнетиков больше протонов будет прецессировать по полю, чем против поля. Другими словами, возникают круговые молекулярные токи (если рассматривать ансамбли протонов). Однако они в основном компенсируют друг друга. Некомпенсированными будут лишь токи, текущие по боковой поверхности цилиндра, и они создают добавочное остаточное поле. Эти токи аналогичны токам в круговых витках или в соленоидах, и поэтому для расчета магнитных полей постоянных цилиндрических (и иных) магнитов можно использовать формулы для расчета полей отдельных витков и соленоидов с током.

При этом будем рассматривать идеализированный случай, когда имеет место однородность магнитных свойств вещества магнетика и напряженность внешнего намагничивающего поля заметно меньше насыщающего значения (в этом случае зависимость намагничивания от напряженности поля линейна). Отметим также, что внешнее поле ориентирует, строго говоря, не отдельные молекулы, а области спонтанного намагничивания (домены), и мы будем полагать, что ориентация доменов является упорядоченной (строго по полю) [7, с. 377].

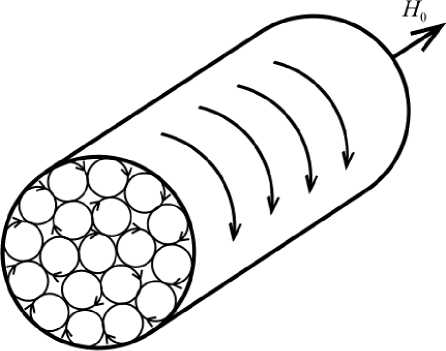
Рис. 1. Постоянный магнит в виде однородного цилиндра с молекулярными токами

диус витка [м], A z = z - z ', причем z ' — z -координата центра витка [м].

Поперечная (радиальная) составляющая равна [8, 11]

H r ^{( z} , r ) =

R A z ² с            cos ф             ,

= C 1T J   ₂--₂----- -----Т^ ф . (2)

² о ( R ² + r ² - 2 Rr cos ф + A z ²)

Интегралы в (1) и (2) берутся аналитически; в результате (ср. [5, 6, 8-11]):

^H z ^{( z} , ^r ) =

C i 1   = х

7 ( R + r ) ² + A z²

R ² - r ² -A z ² ( R - r ) ² + A z ²

E ( k ) + K ( k )

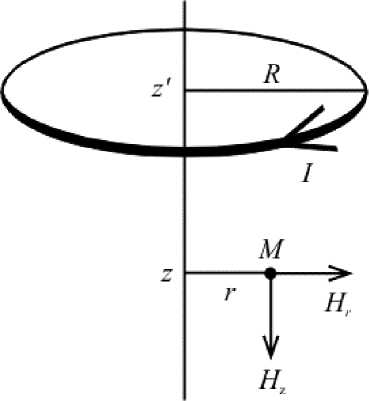
Рис. 2. Тонкий круговой виток с током

ОСНОВНЫЕ СООТНОШЕНИЯ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ

Рассмотрим тонкий круговой виток с током (рис. 2). Продольная составляющая вектора магнитной напряженности, создаваемой витком в точке M ( z , r ), равна [5, 6, 8-11]

H z ( z , r ) =

R ² r           R - r cos ф          ,

= C ¹ V J 7 _{2    2}                     7 \ 3/2 ^{d ф ,} (1)

² о ( R ² + r ² - 2 Rr cos ф + A z ² )

где C 1 = ^ ₀ I/2 n , ^ ₀ = 4 n - 10 ^{- 7} Тл м/А — магнитная постоянная, I — ток в витке [A], R — ра

H r ^{( z} , ^r ) =

----1       1        -------X r ^ R + r )2 + Az2

R ² + r ² + A z ² ( R - r ) ² + A z ²

E ( k ) - K ( k )

где E и K — полные эллиптические интегралы соответственно 2-го и 1-го рода с модулем k = {4Rr/ [(R + r)2 + Az2]}V2,       (5)

равные [12, c. 68, 245]

E ( k ) = J 4 1 - k ² sin ² у d y ,      k e [0,1],   (6)

П 2

K ( k ) = J        ^У , k e [0,1), (7)

о д/1 - k2 sin2 у причем E(0) = K(0) = ti]2, E(1) = 1, K(1) = ~.

Модуль вектора магнитной напряженности, ко торый мы обозначим через Hm (z, r), равен

H m ( z , r ) = | H ( z , r )| = V H z (z , r ) + H r (z , r ) . (8)

Частные случаи

Если точка M находится на оси витка (т. е. r = 0) и R ^ 0, то k = 0 и

H ( z , 0) = С л ₇-------- ^-, H ( z , 0) = 0,

z ⁽ , )      ¹ ( R² +A z ²) ^3/2 , r ,

H_m ( z ,0) = H z ( z ,0).

Если точка M находится на витке (т. е. A z = 0, r = R ), то

H z ( z = z ', r = R ) = H r ( z = z ', r = R ) = = H m ( z = z ', r = R ) = “ .

Значение C ₂ в случае магнита можно определить экспериментально (см. (11)):

Формулы (3)-(10), справедливые для отдельных круговых витков с током, могут быть использованы для расчета магнитного поля цилиндрического постоянного магнита, если представить цилиндрический магнит в виде набора круговых витков с током (см. ниже). При этом одно из отличий магнита от набора витков состоит в том, что константа C , в формулах (1)-(4), (9), равная ^ ₀ I( П для витков, имеет другой смысл для магнита и зависит от материала магнита, а также от напряженности поля при намагничивании магнита [7, с. 373].

C 2 = H z ( z ,0) х

z_r + z            z_r - z

c                 ^+            c

⁽ z c ^{+ z ) 2 +} R ²   V⁽ z c - ^{z ) 2 +} R²

Соленоид

Рассмотрим соленоид — единый намотанный на цилиндр тонкий провод с током (рис. 3). Использование соленоида позволит ускорить расчет магнитного поля на оси цилиндрического магнита. Пусть z c — полудлина соленоида, R — его радиус, n — плотность намотки (число витков на единицу длины, не обязательно целое число). Тогда для продольной напряженности в некоторой точке M ( z ,0) на оси соленоида можно получить следующее выражение (ср. [13, с. 22], [14, с. 215]):

H z ( z ,0) =

где H_z ( z , 0) — измеренное значение напряженности на оси магнита при некотором z .

Соленоид с зазором

Рассмотрим соленоид с зазором (рис. 4). Напряженность в зазоре (в щели) на оси такого соленоида равна разности напряженностей соленоида длины 2 z c и соленоида длины 2 А , где 2 А — длина зазора. В результате напряженность в точке M ( z ,0) в зазоре на оси будет равна (см. (11))

H z ( z ,0) =

z c - z

z„ + z

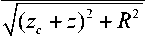
А + z

z c - z ) ² + R²

А - z

-

2     , c --------+ .              -------

_ 7 ⁽ z c + ^{z ) 2} + R^{2      (} z c ^{- z ) 2} + R²

где C ₂ = ц ₀In/ 2, In — плотность тока в обмотке соленоида [ А/м ]; при этом H r ( z , 0) = 0.

Формулу (11) можно использовать для расчета поля на оси как соленоида, так и аналогичного ему цилиндрического постоянного магнита. При этом константа C ₂ в случае соленоида равна ^ ₀ In/ 2, а в случае магнита C ₂ (как и C 1 ) зависит от свойств магнита и процесса его намагничивания.

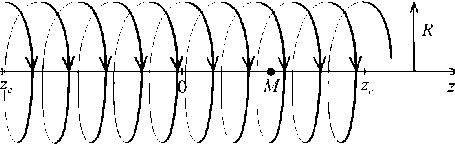
Рис. 3. Соленоид

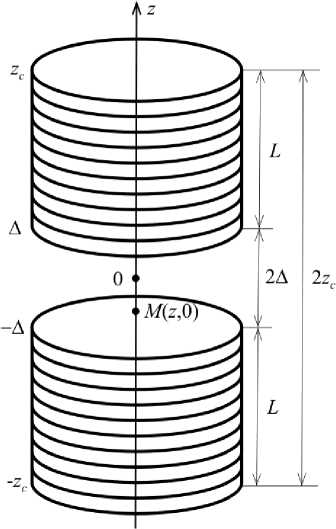
Рис. 4. Соленоид с зазором

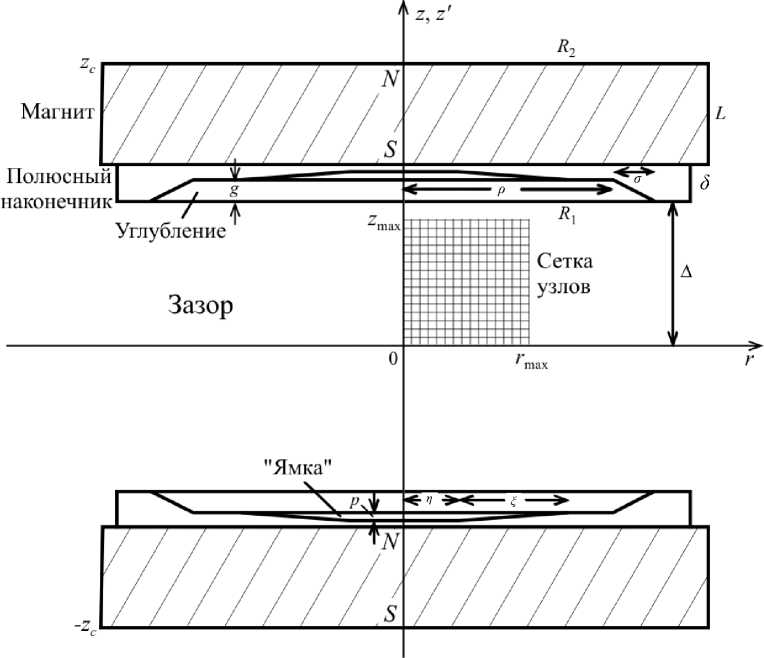
Рис. 5. Постоянный магнит сложной конфигурации

МАГНИТ СЛОЖНОЙ КОНФИГУРАЦИИ

Рассмотрим магнит (рис. 5) в виде двух цилиндров с полюсными наконечниками (pole pieces) и зазором (air gap). Для повышения однородности поля внутри наконечников сформируем углубления (hollows), а внутри углублений — дополнительные углубления, или "ямки" (small pits). В работах [2–4] внутри углублений формируются "горки" (hills), однако "ямки", как показало моделирование (см. ниже), дают более однородное поле. Такой магнит (с зазором, углублениями и "ямками") будем называть постоянным магнитом сложной конфигурации.

Введем следующие обозначения. Параметры магнита: L — длина магнита, 8 — длина наконечника, R ₁ — радиус наконечника, R ₂ — радиус магнита, А — полудлина зазора. Формы углублений и "ямок" аппроксимируем прямыми линиями. Этому будет соответствовать следующая формула для радиуса витка, уложенного в углубление:

R (z) = - (А-| z '0 + р + а , (14) g и формула для радиуса витка, уложенного в "ямку":

R ( z ') = i ( А + g - | z '0 + П + i •      (15)

p

Параметры углубления: глубина g , минимальный радиус р и максимальный радиус р + — ; параметры "ямки": глубина p , минимальный радиус П и максимальный радиус п + i •

Параметры магнита L , 8 , R 1 , R 2 , А будем считать заданными, а параметры углубления g , р , — , p , п , i — подлежащими определению.

Критерий выбора параметров углублений

В качестве критерия выбора оптимальных значений g , р , - , p , п , i используем условие минимума отклонения рассчитанного поля от однородного [5]:

^£ opt = min ^£ ,                   ⁽¹⁶⁾

p      g, р,-, p ,п ,i где

₈ = 1 ^ H z ( z i ,0) - H z (0,0) n + 1 t 0      H z (0,0)

причем n — число дискретных шагов h вдоль z от z = 0 до z = А/2 . Задачу минимизации (16) можно решать, используя известные методы минимизации функционалов без ограничений и с ограничениями на искомые параметры (градиента, Ньютона, координатного спуска, проекции градиента и др.) [15]. При этом ограничения на параметры целесообразно задавать в виде

⁽ u i Ln ^ u i ^ ⁽ u i Lx > i = L-Л ⁽¹⁸⁾

где u_x = g , u 2 = p , u 3 = CT , u 4 = p , u 5 = n , u 6 = £ , а значения ( u_i )_min , ( u_i )_max выбирать, исходя из физико-технических ограничений на параметры, из решения близких задач и т. д.

ПАКЕТ ПРОГРАММ И ЧИСЛЕННЫЙ ПРИМЕР

Разработан пакет программ MAGNET для определения конфигураций цилиндрических магнитов с зазором и наконечниками, имеющими углубления и "ямки" (с целью повышения однородности полей), и для расчета их магнитных полей. Программы разработаны на MS Fortran 5, а графика — на MathCAD, CorelDRAW и PaintBrush. Вычисления запрограммированы с двойной точностью.

Пример

Рассмотрим пример магнита (рис. 5), имеющего следующие параметры (в мм): L + 5 = 250, R 1 = R ₂ = 300, А = 150. Это — заданные параметры.

Для расчета компонент поля H_z ( z , r ), H_r ( z , r ) и H_m ( z , r ) в зазоре задавалась сетка узлов : z е [0, z max ], r е [0, r _max] с шагом дискретизации h = A z = A r = 1 мм, где z _max = r _max = 140 мм. Сначала рассчитывались две функции: H_z ( z ,0) и H_z (0, r ) согласно (9) и (3) соответственно путем суммирования по (фиктивным) виткам, причем поля витков углублений и "ямок" вычитались из полей витков магнита и его наконечников.

Искомые параметры углубления g , p , ст , p , n , ^ определялись путем минимизации (16)-(18) при n = 75. Получены следующие оптимальные значения: g = g opt = ¹⁰⁶ , Р = P opt = ^190.5 , ^CT = ^CT opt = ^92.5 , P = P opt = ⁵ , П = П opt = ^74.2 , ^ = ^ opt = 3.74 мм; e = 8 opt = 0.4493 -Ю ^{- 5} .

На рис. 6 приведены две функции: H_z ( z ,0) и H_z (0, r ) при оптимальных значениях параметров.

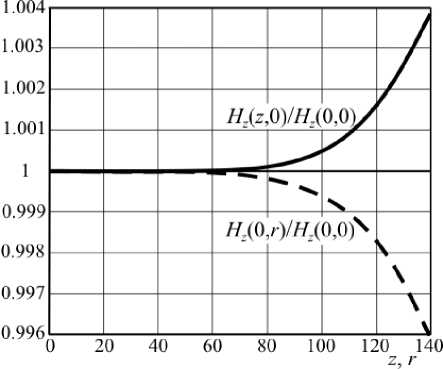
Рис. 6. Нормированные напряженности вдоль z и r при оптимальных значениях параметров углубления

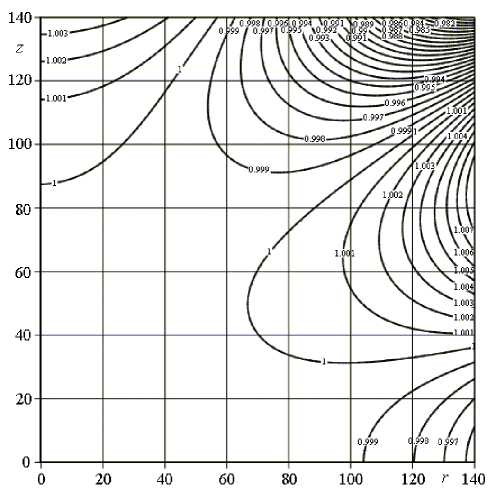
Рис. 7. Изолинии нормированного поля H m ( z , r ) H m (0,0)

Результаты, отображенные на рис. 6, качественно близки результатам японских физиков [2–4]. Однако в работах [2–4] в основания углублений были введены так называемые "горки", а в данной работе введены "ямки", что позволило получить более однородное поле.

Затем были рассчитаны компоненты поля Hz(z,r), Hr(z, r) и Hm (z,r) на всей сетке узлов z, r. На рис. 7 приведены изолинии нормирован- ного поля Hm(z,r)Hm(0,0). Эти результаты качественно близки результатам работы [3].

На рис. 8 для большей наглядности приведены изолинии функции (логарифм относительной неоднородности поля)

I H m ( Z , Г ) - H m (0,0)1 H m (0,0)

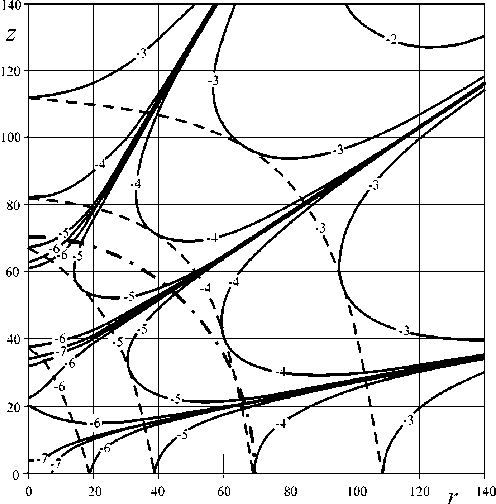
Рис. 8. Изолинии логарифма относительной не- однородности поля

1g [ H ( Z , Г ) — H_m (0,0)| jH_m (0,0) ]

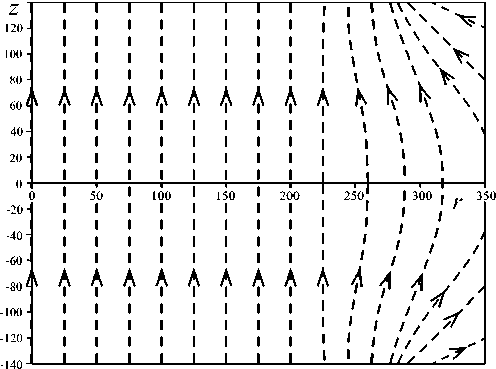
Рис. 9. Линии магнитной напряженности H ( z , r ) (векторные, или силовые линии магнитного поля)

причем непрерывными линиями отображены изолинии, пунктирными линиями — огибающие изолиний, а штрих-пунктирной линией — 50-процентная зона (рабочая зона радиуса А/2).

На рис. 9 приведены так называемые линии магнитной напряженности (касательные к которым совпадают с направлением поля H ( z , r )) [7, с. 320], или векторные ( силовые ) линии магнитного поля [16 с. 44]. Эти линии построены на основе использования команды Vector Field Plot (векторное поле) в MathCAD’е. Может быть использована также команда quiver в MatLab’е. Из рис. 9 видно, что в пределах рабочей зоны [ z _max , r _max ] силовые линии идут практически параллельно, что дополнительно говорит о высокой однородности поля в ней, а на краю зазора (в районе г ~ R 1 = 300) имеет место "бочкообразность" силовых линий.

Замечания

Приведем следующие важные замечания математического и технического характера.

• 1.    Если значения всех 9 параметров L + 5 , R 1 = R ₂, А , g , р , 7 , p , п , ^ умножить на некоторый множитель a >  0, то вид кривых на рис. 6-9 не изменится. Лишь z и r нужно умножить на a . Другими словами, если решен некоторый частный численный пример, то из него можно получить ряд других примеров путем умножения 9 параметров на ряд значений a (без решения этих примеров). Заметим, что на рис. 6–9 приведены результаты моделирования при a = 1.

• 2.    Если постоянный магнит изготовить из мягкого железа, то он будет дешевым, но его поле будет довольно слабым (около 0.2 Тл), и к тому же мягкое железо быстро размагничивается и поэтому потребуется непрерывное намагничивание его с помощью катушки с током простой конфигурации. Можно этого избежать, если использовать высококачественный сплав, например Nd+Fe+B (как в работах [2–4]), но это будет дорогой магнит. К тому же слабость поля не является недостатком (как отмечено во Введении), а изготовление намагничивающей катушки с током простой конфигурации является несложным.

ЗАКЛЮЧЕНИЕ

В данной работе дано развитие методики расчета конфигураций постоянных магнитов МР-то-мографов, создающих высокооднородные поля. Для достижения высокой однородности поля в наконечниках магнитов использованы углубления и "ямки", т. е. рассматриваются постоянные магниты сложной конфигурации. Для расчета полей использована аналогия между постоянным магнитом (а также его наконечниками, углублениями и "ямками") и набором витков с током. Выведены рабочие формулы, разработаны программы и решены модельные примеры, показавшие, что данная методика позволяет получать высокооднородные поля постоянных магнитов с относительной неоднородностью ∆HH~10-5-10-6, т. е. 1– 10 ppm в рабочей зоне.

Данную методику можно рекомендовать для практической реализации в виде дешевого отечественного МР-томографа, предназначенного, например, для обследования детей с целью выявления у них патологий на ранней стадии развития. Длина зазора 2 ∆≈ 30см (как и рабочая зона диаметром ≈ 15 см) вполне достаточна для размещения ребенка, а поле H ≈ 0.2 Тл достаточно и безвредно для его обследования.

Авторы благодарят д.ф.-м.н., проф. Ю.И. Неронова за полезные обсуждения вопросов, рассмотренных в данной работе.

Работа выполнена при поддержке РФФИ (грант № 05-08-01304-а).