О слабой разрешимости смешанной задачи для нелинейного уравнения с псевдопараболическим оператором высокой степени

Автор: Юлдашев Турсун Камалдинович

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 5 (45), 2012 года.

Бесплатный доступ

Изучаются вопросы слабой разрешимости смешанной задачи для нелинейного дифференциального уравнения с псевдопараболическим оператором произвольной натуральной степени.

Слабая разрешимость, интегральное тождество, счетная система нелинейных интегральных уравнений, метод последовательных приближений

Короткий адрес: https://sciup.org/148176933

IDR: 148176933

Текст научной статьи О слабой разрешимости смешанной задачи для нелинейного уравнения с псевдопараболическим оператором высокой степени

В области D рассматривается уравнение

2 m + 1 д4 m + 1 д4 m A n

— + ( - 1) m v ———+ vц ——₂-+-^d-_i- X d t a t a x ² m a t a x ⁴ m a x ⁴ m J (1)

X u ( t , x ) = f ( t , x , u ( t , x ) )

с начальными u (t , x) t=0 =Ф1( x), a j-1 —

—- 1 u ( t , x )| t = 0 =ф J ( x ), j = 2, n 0 t^{J 1}

и граничными условиями

u (t, x) x=0 = Uxx (t, x) x=0 = • • • d 2(2nm-1)

= у x 2(2 nm - 1) u ⁽ t ’ x ) ^x = ⁰ =

= u (t , x )| x=i = uxx (t , x) x=i = • • • d 2(2nm-1)

= — u^M ( t , x ) I x -I = 0, d x 2(2 nm - 1) ^v ,|x = ^l ’

+ ••• +

+УЦ

n ( n - 1) д ⁴ ^nm ⁺ ² ^m ^- ²

^ д n + 4 m

_v a t ⁿ д у ⁴ ^m

дt2 ду4 nm+2 m-4

Ф + n

д 4 nm + 2 m - 1

д t д у ⁴ ^nm ⁺ ² ^m ^- ²

Ф +

д ⁿ ⁺ ⁸ ^m ^- ¹ _ n ( n - 1) д ⁿ ⁺ ⁸ ^m _

Ф + n---:--7— Ф +------„ Ф + atn-1 оу8m 2 atn-2оу8m+2

n ( n - 1) a ⁴ ^nm ⁺ ⁴ ^m ^- ²

+ +---z--- д---д--7 Ф + n

2 a t ² д у ⁴ ^{nm m} ^-4

д 4 nm +4 m -1

g t д у ⁴ ^nm ⁺ ⁴ ^m ^- ²

f Ф^х

где f ( t , x , u ) e С ( D x R ), фД x ) e C ² nm ⁺ ¹ ( D_l ) , = ••• = ^ф (j ) ⁽ ^x )| x = 0 = ^ф j ⁽ ^x ) x = 0 = ^Ф ‘ ⁽ ^x ) x = 0 = = ф/ x )| x = l = ф"₇ ( x )| x = l = ••• = Ф j' nm " ²⁾( x )| x = l = 0, j = L n , D = D t x D i , D t = [ 0, T ] , D i = [ 0, l ] , 0 < l <да ,

l x dydt =| Ф1( у)

д n + 4 m - 1 ---;--;—^x Ф a t n -³ д у ⁴ m + 2

д n + 2 m - 1

0 < T < да , 0 < v , ц - малые параметры, n , m - нату

^+v ( a t ⁿ ^- ¹ д у ² ^m

д n⁴ _

---г Ф + n д t ⁿ ^-1

ⁿ ⁽ ⁿ ^- ¹⁾

• •

Ф + n

д n + 4 m - 2

д t ⁿ ^- ² д у ⁴ ^m

д 4 nm - 3

2 д t д у ⁴ ^nm ^- ⁴

0 n + 6 m - 2

---z Ф + a t ⁿ ^-2 д у ⁶ ^m

n ( n - 1) Ф + —--- x

Ф + n

д 4 nm - 2

д у ⁴ ^nm ^- ²

Ф+

n ( n - 1) д ⁿ ⁺ ⁶ ^m ^- ¹

2 д t ⁿ ^- ³ д у ⁶ m ⁺ ²

Ф+

ральные числа.

Следует отметить, что изучению разного типа линейных и нелинейных дифференциальных уравнений в частных производных и их систем посвящено много работ и при этом применены разные методы [1-3] В данной работе, в отличие от работ [4; 5], используется метод разделения переменных, основанный на поиске решения смешанной задачи (1)-(3) в виде

n ( n -1) д ⁴ ^nm ⁺ ² ^m " ³

⁺ ••• ⁺ - a t д у^{4 nm} ⁺ ² ^m - ⁴

Ф + n

д 4 nm + 2 m - 2

-v 4 nm + 2 m - 2 о у

Ф +

Л Г i - 1 ^

u ⁽ t , ^x ) = lim ^ 1 ¹ —— I a , ⁽ t ) ■ b ,⁽ ^x ), ⁽⁴⁾

N ^^

i = 1

где b i ( x ) =

I 2-3 .

— sin X i x , X i =

i n

Обозначается через W 2 k ) ( D ) множество функций

Ф ( t , x ) таких, что Ф ( t , x ),

5 2 d 2(2 nm - 1)

.. ^Ф ⁽ t , x K-Trn nm -n ^Ф ⁽ t , x ) при ^фиксир^ован- д x 0 x ⁽ )

ном t e D_T принадлежат области определения опера-

•

тора

d 4 nm - 2

a x^{4 nm} ^- ²

, имеют производные порядка k по t ,

принадлежащие L ₂ ( D ), и обращаются в нуль при t > T -5 (0 < 5 - зависит от Ф ( t , x ) )•

Определение. Если функция u ( t , x ) e C ( D ) удовлетворяет интегральному тождеству

Tl '

JJ l u ⁽ ^t , y ) 00

—Ф + n 3 t ⁿ

д n +4 m -1

д n +4 m

д t ⁿ ^- ¹ д у ⁴ ^m

n ( n - 1)

Ф + —-----5--

2 д t ⁿ ^- ² д у

--Ф +

4 m +2 ⁺

n ( n - 1) д ^{4 nm} ^- ²

+ ••• +---5-- 1 —Z7 Ф + n

2 a t ² д у ⁴ ^nm

д 4 nm - 1

дt ду4 nm-2

Ф+

д 4 nm

^ 4 nm S y

Ф+

д n + 2 m

^+v ^ д t ⁿ д у ² ^m

Ф + n

д n + 6 m - 1

д n + 6 m

д t ⁿ ^- ¹ д у ⁶ ^m

Ф+ nn ^- ) ,

2 д t ⁿ ^- ² д у

—ф+ 6 m + 2 '

Г д n +4 m -1 +vu ---: 7— Ф + n

(a t ⁿ ^- ¹ д у⁴ ^m

д n +8 m -2

a t ⁿ ^- ² д у ⁸ ^m

n ( n - 1) a ⁿ ⁺ ⁸ ^m ^- ¹

Ф + —-------7-- Т-Ф +

2 a t n ^- ³ д у ⁸ ^m

n ( n - 1) a ⁴ ^nm ⁺ ⁴ ^m ^- ³ _

+ ■■■ +--- л--Тл --7Ф + n

2 a t д у ⁴ ^{nm m}

д 4 nm + 4 m - 2

-x 4 nm + 4 m - 2 о у

J ф 2 ⁽ у )

+ ••• +

J t = 0

' д n ^-2

---X Ф + n atⁿ ^- ²

д n + 4 m - 3

, 4 m

n ( n - 1)( n - 2) д ⁴ ^nm ^- ⁵

д n + 2 m - 2

^+v[ дt ⁿ " ² д у ² ^m

• •• +

n ( n - 1) a ⁿ ⁺ ⁴ ^m ^- ²

ф +—-— ------ ф +

2 a t ⁿ - 4 д у⁴ ^m ⁺ ²

a t д к⁴ ^nm - 6

д n + 6 m - 3

+ n----7--7— д tn-3 ду6 m

n ( n - 1)( n - 2) д ⁴ ^nm ⁺ ² ^m - ⁵

ф+ n l n zJ)

2 d x

) 4 nm - 4

".---7 Ф +

, 4 nm - 4

Ф +

д t д у ^ nm ⁺ 2 m - 6

n ( n -1) д ⁿ ⁺ ⁶ ^m " ²

—---------Ф + д tn "4 ду 6 m+2

n ( n - 1) д ⁴ ^nm ⁺ ² ^m - 4 )

Ф+— ---------Ф +

О 4 nm + 2 m - 4

² д у J

( n + 4 m - 2

I a _

+v ц -- T—— Ф + n

(a t ⁿ ^- ² a у ⁴ ^m

n ( n - 1) a ⁿ ⁺ ⁸ ^m ^- ²

s t ⁿ ⁴

~ Ф + д у ⁸ ^m ⁺ ²

д 4 nm + 4 m - 5

x----- 7 гФ + a t д у ⁴ ^{nm m}

| ф n - 2⁽ у )

д 2 m + 2

+v --ii— (д 1 ² д у ² ^m

д 4 m + 2

д n + 8 m - 3

д t ⁿ ^- ³ д у ⁸ ^m

Ф +

+ n ( n - 1)( n - 2) _x

n (n-1) a4nm+4m-4 _ v 7 ---------Ф

4 nm + 4 m - 4

dy + ••

^J t = 0

•

д2

Ф д t ²

Ф + n

^+vцVW m

Ф+ n

д 4 m + 1

дtду4m

д 6 m + 1

д t д у ⁶ ^m

д 8 m + 1

д t д у ⁸ ^m

Ф +

n ( n - 1) д ⁴ ^m ⁺ ²

д у ⁴ ^m ⁺ ²

Ф +

n ( n - 1)

д 6 m + 2

n ( n - 1)

д у ⁶ ^m ⁺ ²

Ф +

д 8 m + 2

д у ⁸ ^m ⁺ ²

J t = 0

dy +

⁺ / ф n - 1 ⁽ У )

d d 4 m У d 2 m + 1

—Ф + n— Ф + v ---=-

d t

^д У

d t d y

d 6 m 1

Ф + n ° _c Ф + d y ⁶ ^m J

У d 4 m + 1 d 8 m

+vn ---Ф + n — Ф

(d t a y ⁴ ^m a y ⁸ ^m

J t = 0

dy -

Тогда уравнение u (t, x) = u 0 (t, x) + t N У i-11 в (5)

⁺ f ^lim E I ¹ — yr I ^y ( ^u ) • b ⁽ ^x ) ^p, ⁽ ^t , ^s ) ^ds ,

N ^л“

0 i = 1 V ^1N V

' Г

/ ф n ⁽ У ) ^{Ф + v}

0 _

d 2 m d 4 m

-— Ф + УЦ —— Ф d y ² m d y ⁴ m

- t = 0

для любого Ф ( t , x ) e W 2 n ) ( D ) , то она называется слабым решением смешанной задачи (1)-(3).

В силу (4) из определения смешанной задачи (1) - (3) следует:

l где У (u ) = / y (s , y, u (t, y)) bj (y) dy имеет единст-0

венное решение в классе C ¹ ( D ).

Доказательство. Если u ( t , x ) e C ( D ), то

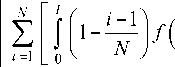
^t , y , ^u 0 ⁽ ^t , у ) ^ь, ⁽ y ) dy

^b i ⁽ ^x )

т. е.

a i ⁽ ^t ) = w ⁽ ^t ) +

t l У N у

+JJ ^y s , У , lim E l ¹

N ^л

0 0 ( J = ¹ 8

< max| / ( t , x , u g ( t , x ))| < g ( t )

j - 1 1

—J a j ⁽ s ) ^b j ⁽ У ) ^х

х P_i(t , 5 ) b i (y ) dyds ;

N 0У i - 1 1

^lim E JI ¹ — ttI ^y ( ^t , у , ^u 0 ⁽ ^t , у ) ) ^ь, ⁽ у ) dy

N ^”

i = 1 _ 0 8 ²

• ^b i ⁽ x ) =

N У i - 1 1

u ( t , x ) = lim E l 1 —— I a i ( t ) • b i ( x ) =

N ^”™l i =1 X7

N У i - 1 1

= km E 1¹ —?rI b i ⁽ x ) ^Г ^w, ⁽ ^t ) ⁺

N ^л™ v /V / i =1 X

= У ( t , x , u 0 ( t , x ) ) ,

t l У n / . 1 \ 1

+ f J ^y | s , У , ^lim E I ^{1 -}A?r l ^a J ⁽ s ) ^b J ⁽ У ) I P ⁽ ^t , s ) ^b i⁽ y ) dyds ;

00 ( N ^“ j = 1 ( N 2 J -

;

причем сходимость равномерна по x для любого t e D T .

Так как функция / ( t , x , u ( t , x ) ) удовлетворяет условию Гельдера, ее частичные суммы равномерно ограничены:

n k--1 n jj - k wi(t) = E ф ki (k~1)! E 6 1-k(v, H) (J - k), • exp {- 9 1,(v ,ц)t}

E / i ( u ) b i ( x )

i = 1

<§ 1 ■! / ( u )|| _c ,

0 < § ₁ = const.

;

X ( n - 1)!( t - s ) n ( A /

P i ⁽ ^t , s ) = ----x--e^xP { ^-6 1 i ⁽ ^v , H ⁾⁽ ^t ^- s ) } ;

⁶ ni ( v , H ) ¹ ’

Рассмотрим следующий итерационный процесс: u k + 1 ( t , x ) = u g ( t , x ) +

6 1 (v, H) =

. 4 nm

‘ N У _i - ₁ 1 _{z x} (6)

⁺ J iim E 1¹ —771^y ( ^u k ) • ^ь, ⁽ x ) ^p, ⁽ ^t , s ) ds ,

N ^л

0 i =18 У

6 ⁿ 0 i (v, H)

6 ^ (v, h ) = ( 1 + v x 2 ^m + vp x 4 ^m ) n .

Теорема. Пусть выполняются следующие условия.

1. Функция / ( t , x , u ) при фиксированном t e D T непрерывна по ( x , u ) e D_l х R и удовлетворяет условию Гельдера по x .
2. / ( t , x , u ) e Lip { g ( t ) | u } , где 0 < / g ( s ) ds <” ;
3. Ц у ( ^t , ^x , ^u 0 ⁽ ^t , ^x ) )|| _c ^ g ⁽ ^t ^).
4. u g ( t , x ) e C ¹ ( D ), где

N У i - 1 1

u 0 ( t , x ) = lim E I 1 —— I w , ( t ) • b i ( x ).

N ^”

= 1

где

■hi ( u k ) = J ^У ( s , У , u k ⁽ ^t , У ) ) b i ⁽ У ) dy , ^k = ⁰, ¹, ²,..... 0

Тогда из (6) следуют оценки

I ^u 1 ⁽ ^t , ^x ) ^- ^u 0 ⁽ ^t , ^x )| I C ₍ D ) <

< / / km E ^У ¹ ^- J^y ( ^u ) b ⁽ y ) dy ^ь,⁽ ^x ) ^p,⁽ ^t , ^s ) ^ds < 0 0 N ^” i = 1 ⁽ N ^

JI l ^/ ⁽ u )l I C ( D )

II ^u k + 1 ⁽ ^t , ^x ) ^- ^u k ⁽ ^t , ^x )|I C ₍ _D )

Г ‘ 1

k + 1

( k + 1)!

J g ( s ) ds

_ 0 -

. (8)

Из (7) и (8) следует равномерная сходимость при k ^л последовательности функций { u_k ( t , x ) }^ _f к

функции u ( t , x ), которая является решением уравнения (5). Единственность решения уравнения (5) следует из оценки

II u ( t , x ) -ϑ ( t , x ) II C ( D ) ^≤

≤∫g(s)u(s,x)-ϑ(s,x)IIC(D) ds, если предположим, что уравнение (5) имеет два решения u(t,x)и ϑ (t,x) в области D и применимj к (9) неравенства Гронуолла–Беллмана.

Статья научная