О собственных колебаниях механической системы каскадного типа, установленной на упругом стержне

Целью данной работы является вывод уравнений движения виброзащитной системы, представляющей собой механическую систему каскадного типа – упругий стержень с установленными на нем последовательно по вертикали на пружинах тремя твердыми телами, а также получение уравнения для определения собственных частот рассматриваемой вибро-защитной системы.

Рассмотрим механическую систему (рис. 1), состоящую из трех масс m1 , m2 и m3 , каскадно присоединенных к упругому стержню с помощью пружин жесткости c1 , c2 иc3. Концы стержня жестко закреплены. Массы m1 , m2 и m3 могут перемещаться только поступательно в направлении осей O1z1 , O2z2 и O3z3 . Здесь точки O1 , O2 и O3 совпадают с поло жениями равновесия масс. Колебания масс характеризуются функциями z1 (t), z2(t) и z3(t). Перемещения точек стержня описываются функцией u(x, t). Пружина присоединена к стержню на расстоянии a от левого конца стержня соответственно.

1.1

Математическая модель механической системы каскадного типа

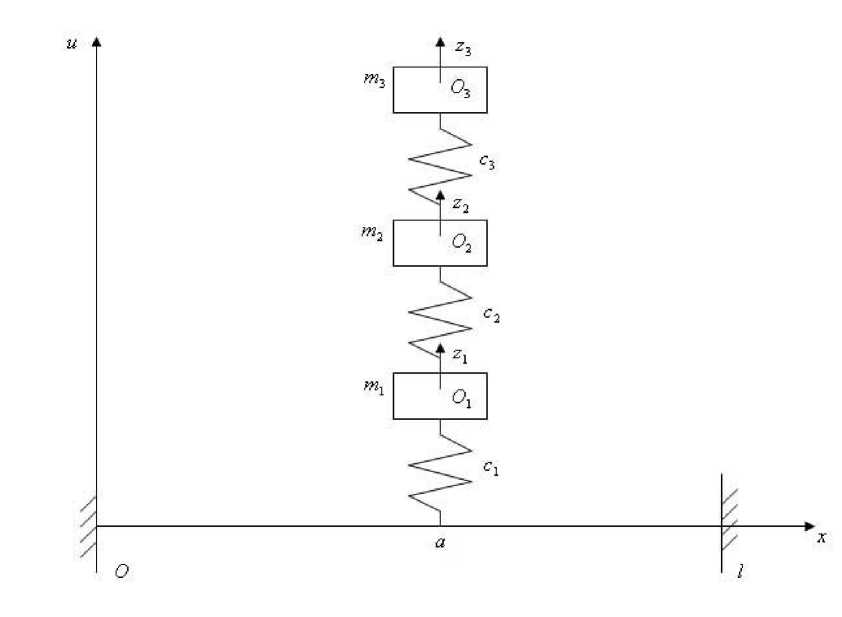
Рис. 1 - Механическая система каскадного типа с тремя телами

Вариационный принцип Гамильтона выражается соотношением:

t ₁

i 5(T - U) dt = 0

(1.1)

t ₀

где T - кинетическая энергия системы, U - потенциальная энергия системы.

Потенциальная и кинетическая энергия системы складывается соответственно из энергии масс, стержня и пружин, т.е.

T _ T1 + T2 + T3 + Tc, U _ U1 + U2 + U3 + Uc, где t 1

_T _ m t ^z 1 ²    _T _ m 2 ^z 2 ²   _T _ m 3 ^z 3 ²

1       2 ■ 2       2 ■ 3       2

U _ c 1 ⁽ z 1 ^- u ⁽ a ■ t ^{)) 2 1}              2

Вычислим вариацию:

, U ₂ = c 2^ z

' 2 ^{- Z} 1 ^{) 2}    _T j _ c 3 ( z

2        ■ ³

l

'3 ^{- Z} 2 ^{) 2}

t 1

i 5(T - U) dt = i 5

2 m ^ +

t 0

l

t 0 V 2

l

dx

l

■ U c = з i EJ

² 0 V

l

2 d u

5 x ² у

) dx

m 2 ^Z 2 +

2 m 3 ^z 3

-

c 1 ( z 1 - u ( a , t )) ²    c ₂ ( z.

-

2___

^z 1 )^{2    c} 3 ^{( z} 3 ^-

-

zl)- +

dx - ¹ j EJ -

20 V

о u

\2

t 1

5 t ² У

,         tr s dx dt = —

* da

^ m 1 ⁽ z 1 + ^a5 z 1 ^{) 2} + m ₂ ⁽ Z ₂ + ^a5 Z ₂ ^{) 2} +

У

t 0

V

+ m ₃( z₃ + a5 z ₃) ²

-

c 1 ( Z 1 + a5 Z 1 - u ( a , t ) - a5 u ( a , t )) ² c ₂( Z 2 + a5 Z.

-

■ ₂ - z 1 - a5 z 1 ))²

-

—

c ₃( z₃ + a5 z₃

—

z ₂ — a5 z ₂)) ²

l

l

+ —

1 r J 52 u       52 u dx — EJJ —t- + a5 —T-

2 00 (d x ²        5 x x

A

dx

dt =

t 1

= j m₁ z_x 5 z_x + m ₂ z₂ 5 z₂ + m 3 z₃ 5 z ₃

—

c ₁( z ₁

—

u ( a , t )) 5 z _x

—

c ₂ ( z ₂

—

z _x) 5 z ₂

—

c ₃ ( z ₃

t о ⁽

⁺ c ⁽ z x

—

u ( a , t )) 5 u ( a , t ) + c ₂ ( z ₂

—

z_x) 5 z 1 + c ₃( z 3

—

z 2 ) 5 z ₂ +

A

⁹ u ^ uu,   \т7_Тд² u _x5² u

+ pF—5 —dx — EJ —-5 —-dx dt

^J₀      5 1 5 1      0     5 x ² 5 x ²

a = 0

—

^z 2 ) 5 z з +

Интегралы, входящие в последнее выражение преобразуем следующим образом:

t ₁

t ₁

j z_x 5 z_xdt = — j z_x 5 z_xdt ,

t ₀

t ₀

t ₁

t ₁

j z 2 ⁵ z 2 dt = ^— j

z₂ 5 z ₂ dt

t ₀

t ₀

t ₁

t ₁

j z₃ 5 z₃ dt = — j

z 3 5 z 3 dt

t ₀

t ₀

t ₁

t 1 l

j c _x( z _x — u ( a , t )) 5 u ( a , t ) dt = jj c _x( z _x — u ( x , t )) 5 u ( x , t ) 5 ( x — a dt

t ₀

^t 0 ⁰

tx j-5u ^uu , ,,    rtx5u 5ux

—5 —dxdt = —5 —dtdx = t о 91    51          0 0 51 5 it{ t0 00

i (

5 u

t ₁

t ₁

A

l t 1

—

l

C5² u „5² u , 5² u „ uu

—v 5 —dd= = —-5—

' 5 x ² 5 x ²       5 x ² 5 x

l

—

l

f 5⁴ u

= —- 5udx ^J ₀ 5 x ⁴

t ₁

j (

—

t о ⁽

^{+ ( —}

⁰ (

t ₀

l

j | 2 u a.dt \ dx = — jj t

t ₀

0 t ₀

5 ² u _л

—— 5udtdx

t ₀

г 5³ u „ uu , l

—_r 5 —dx = —

* 5 x ³    5 x

5 ³ u „ 5 u , 5 ³ u „ —- 5 — dx = —- 5u

5 x ³   5 x     5 x

5 x

l

l

d u

+ —-uddx =

^J ₀ 5 x ⁴

С учетом всех вышеизложенных преобразований, уравнение (1.1) примет вид:

m ₁ z ₁

—

c x ^{( z} x

—

u ( a , t ) ) + c ₂ ( z ₂

—

z ₁

^{)) 5 z} x ^{+ ( —}

m ₂ z ₂

—

c 2 ⁽ z 2

—

z ₁

) ^{+ c} 3 ^{( z} 3

—

z ₂ )) 5 z ₂ +

m ₃ z ₃

—

^c 3 ^{( z} 3

—

z ₂

l

^{)) 5 z} 3 ⁺ j ^{( c} x ^{( z} x

—

u ( x , t ) )) 5 ( x

—

0 (

_a ) _ _{p F} dZu - EJ— ^

^P 5 1²       5 x⁴

A

5 xdx dt = 0

Таким образом, из уравнения (1) вытекает система уравнений движения системы:

m_x z _x + c _x ( z _x

—

u

⁽ a , t ) ^{) —} c 2 ⁽ z 2

—

^z x ) = ⁰

1.2

m 2 ^z 2 ⁺ c 2 ^{( z} 2

m ₃ z ₃ + c ₃ ( z ₃

—

—

z ₁

^{) — c} 3 ^{( z} 3

z 2 ) = ⁰

P F ^u ^{+ EJ} ^u = ^{( c} x ^{( z} x d t       d x

—

^z 2 ) = ⁰

—

u ( x , t ) )) 5 ( x — a )

(1.2)

Исследование свободных колебаний механической системы каскадного типа

Рассмотрим систему уравнений (1.2). Поделив обе части первого уравнения на m ₁ ,

второго на m ₂, третьего на m ₃, а четвертого на p F получим:

где p i =

d ² z ₁ dt ² d ² z ₂ dt ² d ² z ₃ dt ²

⁺ p l2 ⁽ z l ^— u ⁽ a , t ) ^)— p 2l2 ⁽ z 2 ^— z l ⁾ = ⁰

⁺ p 2 2 ⁽ z 2 ^— z l ^)— p 32 2 ⁽ z 3 ^— z 2 ⁾ = ⁰

⁺ p 3 2 ⁽ z 3 ^— z 2 ⁾ = ⁰

-^-u + b^-u = e_x ( z_x — u ( x , t ) ) 5 ( x — a )

2411 tx c          c          c          c           c EJ

:      , p2 = 1 --- , p3 = Д   , p2l = л   , p32 = 1   , b = — , el у ml        mm 2 mm 3        m mi        m m 2      PF

На функцию u ( x , t ) наложены граничные условия:

c ₁

P F

5 u

5 x

5 u d x

Подставив в (1.3) zi (t) , u(x,t) в виде zi (t) = Ai cos pt, i = 1,3 u(x, t) = V(x)cos pt

После преобразований получим:

^— p ² A l ⁺ p l ⁽ A l ^— V ⁽ a ^{)) —} p 21 ⁽ A 2 ^— A l ⁾ = ⁰

<

—

—

^{p 2} A 2 ^{+ p} 2 ⁽ A 2 ^— A l ^{) —} P 32 ⁽ A 3 ^— A 2 ⁾ = ⁰

p ² A 3 + p 3 2 ⁽ A 3 ^— A 2 ⁾ = ⁰

^— p² V ⁽ x ^{) +} b d V 4 x ⁾ = e l ⁽ A 1 ^— V ⁽ a ^⁽ x ^— a ⁾ dx

Граничные условия:

V (0) = V (l ) = 0

dV ( 0 ) = dr ( ) = 0

dx dx

(1.3)

(1.4)

(1.5)

(1.6)

(1.7)

ТЕОРЕМА 1: При любых p , A_l, A ₂ и A ₃ функция

V (x) = V (x — a )el (Al — V (a))

(1.8)

является обобщенным решением уравнения (l.6) , где функции V ( x ) являются решением

уравнения:

2171      d V ( x )

— p V(x) + b    4 ’ = 5(x)

dx

(1.9)

с краевыми условиями:

V ( — a ) = V ( l - a ) = 0 dV       dV                                     (1.10) ( — a ) = ^T(l — a ) = 0 dx       dx

Доказательство:

Отметим, что уравнение (1.6) понимается в обобщенном смысле, т.е. для любой функции ф (, t ) из некоторого класса справедливо:

i ( j - p2V(x)+ b о V

dwi 1 dx ⁴ J

ф ( x , t ) dx = e 1 ( A 1 - V ( a )) ф ( a , t )

(1.11)

Соотношение (1.8) представим в виде:

l

V ( x ) = j V ( x - 5 ) e 1 ( A , - V ( 5 W - a ) d ^ о

В этом случае имеем:

- p² V (. x ) + b dVx ) = j ⁽- p VV ( x - 5 ) + b d * ^{V (}x. - ⁵ ) 1 e ( A - V ( ■ J^K - a ) d 5 dx ^V                      dx J

Следовательно, для любой функции ф ( x , t ) имеет место равенство:

i ( j - Р2 V(x) + 6

о V

dVx ) 1 dx^ J

ф ( x , t ) dx

= j ф ( x , t ) j ⁽- p ² V ( x - 5 ) + b d V ⁽ x ₄ ⁵ ) 1 e_x ( A_x - V ( 5 )) 5 ( 5 - a ) d 5 dx 00 V          d^x   J

Поменяем порядок интегрирования:

i( j - p2 V(x) + 6

0 V

d⁴V ( x ) dx'

ф ( x , t ) dx J

= j e_x ( A_x - V ( 5 )) 5 ( 5 - a ) j ⁽- p ² V ( x - 5 ) + b d V ⁽ x ₄ ⁵ ) Ъ x , t ) dxd § _{0                         0} V                         dx J

Учитывая (1.9), получим:

i( j - p V (x)+b

0 V

d ⁴ v ( x ) 1             V                      V

----^ ф ( x , t ) dx = J e , ( A_x - V ( 5 )) 5 ( 5 - a )J ф ( x , t ) 5 ( x - 5 ) dxd 5

dx ⁴ J               0                           0

Отсюда следует:

l(

j - p ² V ( x ) + b

0 V

d^V C x ) 1 dx * J

ф ( x , t ) dx = e 1 ( A 1 - V ( a )) ф ( a , t )

Что совпадает с уравнением (1.11).

Учитывая краевые условия (1.10), можно убедиться в справедливости того, что (1.8) удовлетворяет условиям (1.7) непосредственной подстановкой.

Таким образом, задача свелась к нахождению уравнения вида (1.9) с краевыми условиями (1.10). Эта краевая задача решается путем представления функции V ( x ) в виде суммы обобщенного решения G ₀ ( x ) однородного уравнения:

2 7FZ \ dd ⁴ V ( x )

- p V ( x ) + b ----= 0

dx и обобщенного решения G ( x ) неоднородного уравнения

2т7( dd V ( x )

- p ^{V ( x ) + b}     ₄* ’ = 5 ^{( x} )

dx то есть

V ( x ) = G ₀ ( x ) + G ( x )

где

G ₀ ( x ) = c 1 S 1 ( p x ) + c ₂ S ₂ ( e x ) + c ₃ S ₃ ( e x ) + c ₄ S ₄ ( P x )

5 1 ( в х ) =

cosh ( в x ) + cos ( в x

5 ₃ ( в х ) =

2 cosh ( в x ) -

2"

^ , 5 2 ( в х ) =

sinh ( в х ) + sin ( в х )

cos fc ) , s 4 ( в х ) =

sinh ( в х ) - sin ( в х )

функции Крылова, c 1 , c ₂, c ₃, c ₄ - неизвестные постоянные, которые находятся из краевых условий. Частное решение G ( х ) можно представить в виде:

G ( х ) = е ( х ) ,                             (1.12)

где 0 ( х ) - это функция Хэвисайда, а в =     .

b ⁴

Действительно. Представим (1.12) в виде G(х) = 0(х)f (х), где f (х) = '‘d) • f (°) = f'(°) = f ’(°) = f '(0) =1 ьв                              b

Известно, что

(Ф х )f(х )) = 9'к х )f(х) + ^( х )f'(х ) = Ф х )f(х) + ^( х )f'(х )

то есть j (^(х)f (х)) ф(х)dx = j 5(х)(х)f'(хф(х)dx + j 0(х)f'(хф(х)dx =

= f (°ф(°) + j 0( х)f'(х ф( х) dx = j 0( х)f'(х ф( х '^х или

^(0(х)f (х)),Ф(х)) = (^(х)f'(х)Ф(х))

Отсюда:

(Фх)f (х)) = 0(х)f,(х)

Аналогично получим:

(^(х)f (х)) = 6(х)f"(х)

‘ ( 0 ( х ) f ( х )) ⁽³⁾ = 0 ( х ) f <³⁾ ( х )

(^(х)f (х))(4) = (^(х)f (3) (х)) = ^'(х)f (3) (х) + ^(х)f (4) (х) = 5(х)f (3) (х) + 0(х)f (4) (х), то есть j (^( х) f (х ))(4) ф(х) dx = j S( х)f<3) (х )ф( х) dx + j ^( х)f(4) (х )р( х) dx =

= f ^<3) ( ° ) ф ( ° ) + j 0 ( х ) f ⁽⁴⁾ ( х ) ф ( х ) dx = ^ °- + j 0 ( х ) f ⁽⁴⁾ ( х ) ф ( х ) dx =

= f ^(х) ф( х) dx + Г ^( х)f<4) (х )ф( х) dx = ff ^х) + ^( х)f<4) (х )1ф( х) dx b                                         b              X или

((0(х)f (х фф ф(х ))=f ^(х) V b

+ 0 ( х ) f ⁽⁴⁾ ( х ), ф ( х )

отсюда

(е( х)f (хГ = ^(х)+е(х)Г41 (х)

b

Подставляя выражение для G ( х ) в левую часть (1.9), получаем:

— p ^(xx)f (x) + bf ^x- + 0( x)f(4) (x)) = - p ^(xx)f (x) + bf ^x- + 5(x)e 4 f (x) V b              )                  V b

= - p ^(xx)f(x) + 5( x) + ^(x be 4 f(x) =(— p2 + be 4 )0(x)f(x) + 5(x) =

V

n 2 ^

p + b- 0( x)f(x)+ 5( x ) = b v

(— p2 + p2 Иx)f(x) + b(x) = b(x),

5 ( x ) = 5 ( x ) .

Таким образом, функция G ( x ) удовлетворяет (1.9) в обобщенном смысле.

Подставляя в равенство (1.8) x = a, получим выражение для V ( a ) :

V ⁽ a ) =

V (0> i A i 1 + V ( 0 ) е 1

(1.13)

где V(0) = c 1. c 1 можно найти из граничных условий (1.10), решив систему линейных алгеб- раических уравнений относительно c1 , c2 , c3 , c4 .

Подставляя (1.13) в уравнения системы (1.5) получаем систему:

p 12 — p ^{2 +} p 212 — p 12 1 VjV ⁰)^ ^ A 1 — p 212 A 2

= 0

- p 2 A 1 ^{+ (} Р 2 - p ^{2 +} p 32 ) ^A 2 - p 32 A 3 = ⁰

^- p 3A _г ⁺⁽ p 3 ^- p ² ) A 3 = ⁰

или

Отсюда получим уравнение для собственных частот:

p 22

1 + Т Ж "  p ⁺ p 21      — p 21

2        2  2,2

^- pг          pг ^- p ⁺ p 32

^{0                  -} p 3 2

— p 32

p 3 ^- p

= 0

-^1

V 1 + V ( 0 ) ^ 1

—

2 .

p ⁺ p 21

(    1    1

( p 2 p 3

V

22    2    2     2

— p (p + p 2 + p 3 + p 32 )) +

(1.14)

⁺ p 212 p 2^{2 (} p ² - p 3 2 ) = ⁰