О спектре семейства интегральных операторов, определяющих симплектическую квантовую томограмму

Фурье, спектр интегрального оператора.

В данной работе мы рассматриваем семейство

интегральных операторов пространство H = L ²(R). тельные параметры, v = 0.

А

Fд, определенных в

Здесь р. v

— действи-

∞

-—г ei^^ / e ^{- i} ‘^{2 —} \v\5 ( t — x ) ф ( t ) dt = ф ( x ) . \v\

-∞

А

F д,, [ Ф ]( x ) =

e

V 2 n\v\

µx ²

ⁱ 2 ν

∞

µy 2 eⁱ 2

-∞

Итак,

-

xy iv ф (y) dy (1)

А

F

- - 1

µ,ν

= F д,

A

V = F

∗

µ,ν

A I

= F ⁺

µ,ν ^.

Обозначим x и p

стандартные операторы

Видно, что при р = 0, v = 1 действие оператора

координаты и

есть прямое преобразование Фурье. Мотивировка.

ранстве H по формуле

импульса, действующие в прост-

исследования такого семейства, связана, с тем, что

функция

( Х f )( x )= xf ( x ) , ( Pf )( x ) =

i ddx ^{f ( x} ) ■

^{щ ( x} ,p, ^v ) = \ ^F д,, ^{[ ф ]( x} ) \

А f Е H. Вычислим действие для композиции Fд,,

представляет собой симплектическую квантовую томограмму [1] состояния с волновой функцией ф.

и наблюдаемой px + vp:

( ^F д,, • ⁽ P ^{x +} / щф ^{ф ]( x} ) =

Из определения сразу можно увидеть некого-

А рые свойства оператора Fд, линейность и уни-

I-

—

А тарность. Линейность очевидна. Оператор Fд,,

является композицией умножения па. единичную по модулю функцию и преобразования Фурье, поэтому сохраняет норму в L ² (R).

Существует обратный оператор F - , = F_д, В самом деле:

-v-

e

V 2 n\v\

∞

µx ² i 2

-∞

e

µy ² xy _i µ ₂ yν _{- i} x ν y

µ        µx ²

_e ⁱ 2 ν

V 2 n\v\

∞

-∞

ν

µy

d dy

) ^{ф (} У ) dy =

iν

p 2 n\v |

e

² µx ⁱ 2 ν

Fµ,ν

A

• F F д,

v ) ^{[ ф ]( x} ) =

e

2 n\v\

² µx ⁱ 2 ν

∞

/

µy ² e^{i 2 ν}

-

xy ⁱ ν e

-

µy ²

* 2 v X

∞

µ        µx ²

e^{i 2}

V 2 n\v\

-∞

µy ² e^{i 2 ν}

-∞

х

∞

µt2    yt e-i—+ i — ф(t) dt dy =

iν

2 n\v |

∞∞ _e i µ 2 x 2

-∞ -∞

∞

2 n\v |

∞ µx ² eⁱ 2 ν

-∞

2 n\v \

∞ µx ² ei 2

-∞

µy ² eⁱ 2 ν

-

∞

e

-∞

-

i "y У ^{ф (} y ) dy

µy ² xy _i µ ₂ y _{ν - i} xy

ν

i xy У ^{ф (} У ) dy

V 2 n\v |

7" ^{ф (} y ) dy = dy

2       2

µx µy xy e    ei2v7-i—ф(y)

∞

+

-∞

µt t-x e- 2— e ~yф (t) dtdy =

iν

+ / e

V 2 n\v \

² µx ⁱ 2 ν

1 dy ( e * '^ - "y ) Ф ( У ) dy =

-∞

e

-

e

∞

µt2                   t-x i 2 — ф (t) dt e — y dy =

∞

µ        µx ²         µy ²

_e ⁱ 2 ν        _e ⁱ 2 ν

V^{2 n} \ ^v \

-∞

-

xy i ~ Уф (У) dy +

-

µt2         t i 2 — 2n5( -

ν

x

— J ф ( t ) dt =

iν

+ / е‘

V 2 n\v \

∞

² µx i _{2 ν}

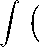
µy i

ν

-∞

x i

ν

µy ² _e i ₂

-

i "y Ф ( У ) dy =

Работа первого автора частично поддержана грантом № 2.1.1/12136.

А В ЦП «Развитие научного потенциала высшей школы»

µ

V² ^У |

µx ²

e^{i 2 ν}

∞ j e “yT-i У уф (y) dy-

-∞

∞

µ        µx ²

_e ⁱ 2 ν

V^{2 n | v |}

-∞

µy ² eⁱ 2 ν

-

i ' У^{ф (} у ) dy ⁺

+

x p2n|v|

∞ µx ² ei 2 ν

-∞

ei “y i y ф ( у ) dy =

x p2n|v|

∞

µx ²       µy ²

eⁱ 2 ν eⁱ 2 ν

-∞

—'

xy

■ i^V ф ( y ) dy

A

F^,v ^{[ ф ](} x ) -

A

Теперь имеем свойство оператора F^,_v:

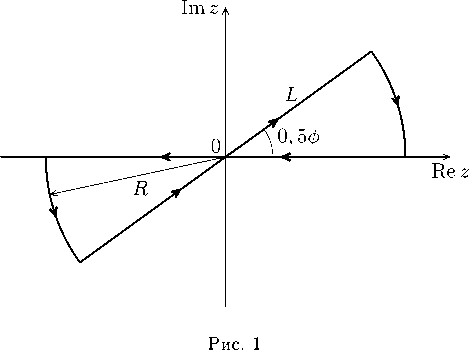
F+vxF ^,V = Mx + VP-(3)

Из последней формулы следует

А .А

F + ,v Р F ^ =

= ~ ^F Ц - v ⁽ Mx - ^V P ) ^F + - v ⁺ V ^F + vx ^F ^,v =

= — X + — ( цх + vp ) = —-- X + цр. (4)

νν     ν

Рассмотрим контур в комплексной плоскости, изображенный жирными линиями па. рисунке. Он состоит из отрезка прямой L , отрезка действительной оси и дуг окружности радиуса R с центром в начале координат. Интеграл по C r стремится к

Основной нашей задачей является поиск собст-

А венных функций и собственных значений F^,v. А

Вначале установим, как действует F^,_v на осиов- x ²

ное состояние квантового осциллятора e ² .

Предложение 1.

Р_ИЛ e^-^ ] = ,    ¹   = e ⁽ i^ ^- — “ ) 2 v

µ,ν

V^{1 и} (1 —i ^ф

(под корнем будем подразумевать такой, что его действительная часть положительна).         □

x ²

Замечание. Видно, что в общем случае e ²

не является собственной функцией оператора.

пулю:

| j e ^- z ² - i kk dz| 6 j | e ^- z ² - i kk dz\ =

C R                C R

= j | e ^- ^ | • | e i k k | . | dz | .

C R

Ila C r выполИЯСТСЯ z = Re ^iф. 0 6 ф 6 2 V- Сделаем оценки:

| _e - z 22 | = | _e - R 2r e ^{2 1ф} | = | _e - R 2² (cos^{2 ф} + i sin^{2 ф} ) | =

22    22

_ e - ^2- cos 2 Фe - R2~ i sin 2 Ф   e - R2" cos 2 Ф 6 e - R2~ cos ^

z ²

cos v =    / ., T- еле довательно. | e 2 |

У ц² + v ²

- R2

6 e ² ^“ 2+ ^ 2.

Доказательство.

x ²

F M,v [ e - "2" ]

e

V 2 n|v|

∞

2 f 2 µx2        µy2 xy i 2ν       ei 2ν -i ν

-∞

y ²

e 2 dy =

- i √ ^xz

^| e     'e^{v v}

| x | R

/

V^{2 n | v 1}

∞

µx ²

ei 2 ν

= exp

|x|R

-∞

(iµ-ν)y2    xy e 2ν i ν

dy =

Итак,

V ^V ^^{1 +} V2 )

6 ex^p ( XR)-

p2 n|v|

∞

µx ² ei 2 ν

-∞

y ²

- α ₂

xy

- i ^xy ν

dy.

j ^| e- ^Ы

C R

e

:- i V z ^| • \dz ^| 6

В последнем интеграле сделаем замену: z = yV&, Re уаУ >  0. a = 1 — i V. Eели a = |a|ei^v. тогда, интегрирование будет вестись по прямой L, наклоненной к действительной оси на угол у/ 2 (см. рис. 1):

∞ 2 2

,     e^l “v     e ^{- a} yr ^{- i} V dy =

■ J y

-∞

1       ,.“- ² Г _z 2_ г -z dz

=    ,        ei 2 v     e ² i v a „        .

yj 2 n|v|      J             y/&

R ²      ν              |x|R

6 ^exp Г т vy+V 2 ^exp( —)j'^dl' ⁼

C R

( R ² v !     f | X | R

=^exp E “ vy+v2 ) ^exp( —)^R¥'

lim exp f - R 2        ! exp f xR ) R, = 0 .

R ^^       2    ц ² + v ²         V

- ^{z 2} - i ^xz

Функция f ( z ) = e ^{2 v a} v регулярна во всей комплексной плоскости, поэтому интеграл по «жир-

пому» контуру равен пулю:

j f ( 2 ) dz +

L

-∞

/ f ( z ) dz + lim / f ( z ) dz = 0 .

R →∞

A

Используем ранее полученное свойство F^,_v ( цX +

A

+ vf)) = xF^,_v и его комплексное сопряжение

А                             А

^{F +}v ⁽ Ц ^{X —} ^p) = ^{xF +},v'-

+ ∞

C R

Мы показали, что последний интеграл равен пулю, следовательно,

+ ^ц . +

^F ^,VV = V ^F ^,vx

+

ν x µ,ν ^,

j f ( z ) dz =

L

-∞

+ ∞

A .         A                  A .        A aF +,v X F+ eFtv Р F

А такой

интеграл

e

V 2 n|v |

∞

µx ² i 2 ν

-∞

e

— j f ( z ) dz = j f ( z ) dz.

a ।               a               _ a । a

++ a ^,v + x ^,V + в v ^,Vx ^,V

/3 , , , в pt

ν x ^F µ,ν ^F µ,ν ^,

+ ∞

-∞

легко вычисляется и известен:

А .         А               А .      А

^F + ,v ^xF ^,V = ^F + ,v ^F ^,V ⁽ Ц ^{Х + vp )} = Ц ^{Х +} Vp,

z ²

-

i x = z dz

1~-1

α

,₊ x — ip a ^t =

2^

µβ a + в - (ЦХ + vp)--x.

e ^{a | v |}

_i µ ₂ x _ν

1        i ^^{x 2}

ei 2ν e a|v|

x ²

- 2 a v ^{1 2}

∞

e

z ²

-i √x z e vQv dz =

Подставляя ц = cos 2 — , v = sin 2 — и приравнивая коэффициенты, получим систему

a cos т П — в sin

π

-∞

^{a l v} I

e ⁽ in - — ц ) xv

a ^siⁿ 2n + в cos

π

2 n

.

i

.

Положим ц = cos 2 — , v = sin 2n- тогда

Решение системы:

a = A e ^{- i} 2 n , в

V2

i π _e - i _{2 n}

V2

.

A

^F cos П , sin П ^[ e 2 n ^,    2 n

x ²

^{2 ]} =

Tsina n

i cos π 2n e i cos П

π 2 n

-

i cos ^π 2 n

x ²

2 sin ^π 2 n

Теперь мы можем найти собственные функции.

Теорема 1. Волновые функции возбужденных состояний осциллятора.

=

i

i ^sin 2n ^+cos 2n

i cos ^π - sin ^π

_· e        2 n        2 n

-

i cos ^{π x 2} 2 n 2 sin ^π

2 n

1  (а+) ^m

Vm ^{( x} ) =       r-; ^e

x ² 2

х/П V 2 m

Hm ( x ) e m !

x ² 2

= \j ei 2 ^{(1 -} n ) e^-

x ² 2

ei 4 ^{(1 -} П ) e ^- x² .

являются собственными

ZS

функциями оператора.

F cos n , _sin - n , отвечающие собственным значениям

Это означает, что волновая функция основного состояния осциллятора, будет собственной для one-А

^A m ^e

-

i ^πm 2 n

.

¤

I-

ратора F cos 2 n , _sin - n . Так ли это для возбужденных уровней осциллятора? Введем стандартные операторы рождения a ' и уничтожения a по формуле

Доказательство. Утверждение может быть доказано по индукции.

Утверждение верно для m = 0 с собственным значением A 0 = 1 в силу предложения 1. Пусть

,₊ x — ip a ^t =        ,

V2

A I ' A

X + ip a = --=—

V2

.

верно для m с собственным значением Am . докажем для m + 1. Используя предложение 2, получаем

^™

—

Рассмотрим операторное

^A -I-произведение F^,_v н⁺.

Линейная комбинация операторов координаты и импульса, при преобразовании переходит в линейную комбинацию этих операторов. Попытаемся найти оператор b ⁺ = ax + вР , такой, что

A

^F cos П , sin П ^{[ V} m +1^] = 2 n    2 n

A

F m +1

cos П , sin П a +^{[ V} m ^] = 2 n     2 n

e i 2 n a +

/   . ! a Fcos П ,sin П [Vm] = m+ 1       2n   2n

A

Fµ,ν

+   at p a      ^b F ^,V.

_e - i ₂ ^π _n

V m + 1

a^t ( Am^m )= Ame i n Vm +1 .

Предложение 2.

Теперь рассмотрим оператор

так что

F

b ^t = e ^{- i} 2 n a ^t ,

A ф n

π1                       n i4 (n 1)

e ^{4 n}     F cos ₂ ^π _n , sin ₂ ^π _n

.

π cos n,sin n a = e  2n a Fcos n,sin n

2 n ^,   2 n                            2 n ^,   2 n

.

¤

Доказательство. Заметим, что

x ²

Тогда e "2 является неподвижной точкой преобразования

А ф n [ f ]( x ) =

a ⁺ = F t v b ⁺ F ^,v = F t v ( aX + вР ) F^ =

= aF t v X F ^,v + eF t v

А

. pF ^v.

n

1 — i ctg ( ту— I 2 f 2 = t         V 2n) e ^v

N 2 nJ

-∞

-

i xy f ( y ) dy. (5)

Обозначим к Тогда.

VsH n -i ^cos 2 П =

ei П (¹ - 1).

p2 pv |

x ²            x ²

kF cos , sin ⁿ [ e ² ] = e ² 2 n ^,    2 n

⁽_M_1 ⁾ P V 7 2 e^{i 2 ν µ - µ}                e^it dt.

-∞

Заметим, что

/ A               \ ^П

I kF cos n , sin n j ^A = e 2 n ^,    2 n

-

_i π ₊

2 a   kF cos n sin n cos 2n ,s 2n

)"

+ ⁿ

• ia    kFco       n , cos 2n ,sin 2n     ,

так что pm так же являются собственными функциями Ф _n , отвечающими собственным значениям ( —i ) m. Следователыю. оператор Ф _n является обычным преобразованием Фурье. Тем самым преобразование

е i п (П - 1)р       • - e             cos π ,sin π

2 n ^,    2 n

является корнем n-й степени из преобразования Фурье. Такое преобразование называется дробным преобразованием Фурье и было введено и подробно исследовано в [2].

Теперь вернемся к рассмотрению общего one- x ²

ратора. Результат действия F^,_v [ e ² ], полученный в предложении 1, наталкивает на. мысль, что собственную функцию F^,_v нужно искать в виде ax ²

e ² v , где a — некоторая, вообще говоря, комплек

сная постоянная.                    ___

1 - µ ²  2

Предложение 3. Функция e ² v x является собственной функцией оператора F^,_v.    □

Доказательство. Рассматривая действие ax2

F^,_v [ e ² v ] и проводя рассуждения, аналогичные приведенным в предложении 1, получим

F. [e-aX2 ] = , 1 e(■ a—-) x2 , p а (a) Iv I где a (a) = a Pi1. Приравниваем показатели экспонент i^--— = —a и получаем a = р1 — д2.               ■

В зависимости от значения д значение a может быть либо действительным, либо мнимым. В случае действительного a (будем считать a >  ax ²

> 0) фуикния e ^- 2- е L ² (R) и. следовательно.

F ц, _v [ e ^- ax⁷ ] существует. В случае мнимого a ax ²

функция e ^-2^ / L ²(R), тем не менее функция F^,_v [ e ^- a²^ ] определена. Более того. F^,_v [1] также существует (в смысле того, что интеграл сходится). Это легко показать простым интегри

рованием:

∞

F [1]( x ) = p= eiei ^{- i v} dy =

Р ² ^^{| v 1}

-∞

1 p 2 n|v|

µx ²   _{- i} x ²

e^{i 2 ν} e ^{2 µν}

∞

J e¹ ( P — ^{y -} p ^- ) dy =

-∞

Последний интеграл вычислим с помощью интегралов Френеля:

∞

∞

I eit ² dt = 2 1 ⁽cos t ² + i sin t ²⁾ dt =

-∞

= 2

^{(1 +} i >  p

Следовательно,

^F ^,v ^{[1]( X} ) =

= \1 ^{1 V ex}P f iT ( д д v       2 v

Аналогично для мнимого a = i|a|:

А

^F H,v ^{[ e}

=

1)+ i µ

ax ²

² v ] =

µ - |a|

учитывая, что

^{| v 1             X 2 (}

V ^6XP i 2 v ( ^д

^{| a |} = Рд ^{2 — 1} •

—¹  ) ⁺ i

µ - |a|

П)'

А

^F H,v ^{[ e}

ax ²

² v ] =

= У ( д + Р д ² — 1) |V| exp

f ^{— i}x- Рм 2 2 v

¹⁺ i ⁿ)^-

Итак, найдена одна, собственная функция общего оператора. Естественно предположить, что это не единственная собственная функция. Попытаемся найти оператор b (в виде линейной комбинации X и р ), удовлетворяющий соотношению

А     А       А А

F b = AbF -

Предложение 4. Операторы

ь = р2

1 — ν ²

1 ^x ±i 4I²

ν ²

- „ 2 p

)

удовлетворяют соотношению

А     А       А А

F b = AbF -

¤

Доказательство. Будем искать операторы в виде

Тогда.

A         A . A A b = AF+,v bF

А

A b = ax + вР-

A .                             A

= AF + ,v ( aX + вР А F

А .          А

= A ( aF + ^ X F

A .         A

+ eF + ,v Р F ^,v ) -

А

А

А

A        A            A        A

Действия F + ^XF^,v и F + ^XF^,v выше (3) - (4), так что

A .         A                  A ।        A

A ( aF + ,v XF ^,v + eF + ,v pF ^,v ) =

= A ^a ( дX + vp ) + в Q"

µ ²

= A I aд + в —

² — 1

x ν

ν

найдены нами

+ дР =

—^ X + А ( av + вд ) Р-

Приравниваем коэффициенты при каждом операторе и получаем систему уравнений

Г а ( Ац — 1) + вА ^ - 1 = 0 ,

[ аАv + в ( Ац — 1) = 0 .

По правилу Крамера, эта. система, имеет нетривиальное решение при

( Ац — 1)2 — А ²( ц ² — 1) = 0 ,

А2 — 2 цА + 1 = 0, т. с. при А = ц ± ц2 — 1. Обоз начни А 1 = ц + + л/ ц2 — 1 и А2 = ц — Vц2 — 1. При А = А 1 имеем

£ + i 4/ 1 - ^ ₂ p^ , а при А = А 2

b 1 =

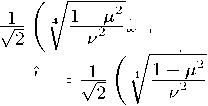
А x-

i 414Б4

ПОЛУЧИМ b 2 =

Посмотрим, как действуют эти операторы на.

собственную функцию:

^f о⁽£) = Ф ^exP ( ^— ^ ^{ц £} 2 ) =

4 п           2 v     /

= -4 ^exp ( ^— 2 ^{Y 2 £} 2) .

Легко видеть, что b 1 f 0 = 0 и b ₂ f _о = \/2 Y^f о, а также F^,vb 2 f о = А 2 b 2 F^,_vf о = А 2 b 2 f 0. II вообще

F ^ bnf о = А nbnf 0.

Итак, найден спектр (набор собственных функций) оператора F^,_v: fn = bnf о .

Целесообразно назвать b ₂ оператором рождения и обозначить b ⁺.

Заметим еще один интересный факт: пусть xˆ - ipˆ a+ =   ^2— обычный оператор рождения.

Пусть а+ = -^2 (y£ — у dx) имеет смысл оператора рождения на растянутой в y раз оси. Тогда b+ = а+, где Y = У 1 -2^ - ПР1140211 fо(ж) = Фо(Y£)• г,те фо — волновая функция основного состояния осцил лятора.

Итак, нами доказано следующее утверждение.

Теорема 2. Набор нормированных собственных функций оператора F ^,v пр и |ц| < 1 и v = 0 имеет вид fn(£) = (—n (b+)nfо) (£) =

= 8. / 1 — ц ²    1 М ( 4/ 1 — ц ²

V п ² v ² — 2 nn ! n у V v ²

µ

2 ν ^x . ¤

Замечание.

Операторы b 11 b+ удовлет воряют каноническим коммутационным соотношениям

[ b,b ⁺] = 2 ^ y£ + Y p) Y^— — 4^

2 ( ^{y£ —} ip) (^{7 i+} i^p ) ⁼ [

i

- p,Y ^£ = ^γ

—i [ £,p ] = —i ² = 1 .

Вычислим дисперсии координаты и импульса, в состояниях с волновыми функциями f_n ( £ ):

+ ∞

( D^£ ) n = - fnI^{£ 2} Ifn® = У £ ² fn ( £ ) d£ =

-∞

+ ∞

= Y I ^{£ 2} 4n ⁽ Y^£ ) d^£ =

-∞

+ ∞

- 12 У ⁽ y^{£ )2} 4n ⁽ Y ^£ ) d ⁽ Y ^£ ) =

-∞

+ ∞

= Y 2 у t ² ^n ⁽ t ) dt = Y 2 у+2) .

-∞

Здесь Ф п — волновые функции состояний гармонического осциллятора, а, как известно, диспер-

)-

I-

сии координаты и импульса осциллятора на n-м возбужденном уровне равны (n + 2 ). Аналогично для импульса:

( Dp) n = - fn|p ² Ifn ® = / fn

d ²

d£ ² fn/

= Y ² fn

d ²

d ( Y£ )²

fn )= ^{y 2} ( " ⁺2) •

Таким образом, в зависимости от значений параметров ц, v дисперсии могут принимать любые положительные значения:

( D£ ) n

( Dp) n

= \Rц ( n ⁺ 2 )

= 444 ( n ⁺ 2) .