О способе определения бортовой эфемеридной информации L1OC, L3OC ГЛОНАСС в целях тестирования алгоритмов местоопределения в навигационном приемнике ГЛОНАСС

Цитирование: Шарфунова, Т.Г. О способе определения бортовой эфемеридной информации L1OC, L3OC ГЛОНАСС в целях тестирования алгоритмов местоопределения в навигационном приемнике ГЛОНАСС / Т.Г. Шарфунова, Д.А. Красильникова // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(7). С. 788–802. DOI: 10.17516/1999-494X-0228

никах. Если не требуется отработка точности навигационных определений по НС L1OC, L3OC, то для генерации НС могут быть использованы опорные эфемериды НКА ГЛОНАСС, предоставляемые в апостериорном режиме Центрами обработки СВОЭВП и ЦНИИМаш в формате SP3 файлов. Указанные эфемериды рассчитываются по сложным моделям движения с учетом большого числа возмущающих воздействий на движение НКА, обеспечивают наивысшую точность расчета положения НКА на опорные эпохи, но не обеспечивают высокие точности расчета положения НКА по алгоритмам потребителя, так как в навигационных приемниках для расчета положения НКА используют более простые модели.

В составе навигационной оперативной информации L1OC, L3OC предусмотрена передача согласованных эфемерид НКА, которые на те же моменты времени t b должны быть рассчитаны на основе опорных эфемерид таким образом, чтобы методические ошибки прогнозирования по более простым моделям движения НКА, используемым потребителем, в среднем на интервалах до 15 мин от опорной эпохи t_b были минимальны.

Кроме этого, в составе неоперативной информации НКА «Глонасс-К2» планируется передача ПДМД НКА, которые должны обеспечить точность расчета положения НКА по упрощенным алгоритмам потребителя не более 1 м на интервалах расчета положения НКА до 4 ч.

Целью работы является совершенствование определения ПДМД НКА для целей моделирования навигационной информации по перспективным сигналам L1OC, L3OC системы ГЛОНАСС.

Задача определения ПДМД НКА ГЛОНАСС сформулирована как нелинейная задача построения согласующей модели на мерном интервале 4 ч. Использование классического МНК для определения ПДМД не позволяет получить эквивалентные по точности решения системы условных уравнений при изменении начальных условий и/или количества итераций. Как показал анализ, указанная задача неустойчива и относится к классу некорректных задач. В связи с этим для определения ПДМД был применен метод регуляризации по А.Н. Тихонову, основанный на применении дополнительной априорной информации. Результаты решений протестированы сравнением расчетного положения НКА ОГ ГЛОНАСС по уточненной (в части скоростей и ускорений) ЭИ, ПДМД и окончательных опорных эфемерид SP3 СВОЭВП. Примененный способ позволил получить устойчивые решения для 12 уточняемых параметров долговременной модели движения НКА. Максимальная погрешность расчета положения НКА ОГ ГЛОНАСС на интервалах до +4 ч от опорной эпохи t_b не превысила 0,2 м по более чем 5700 реализациям уточнения ПДМД.

Определение согласованных эфемерид и ПДМД НКА ГЛОНАСС для генерации навигационного сообщения L1OC, L3OC

При определении местоположения в навигационном приемнике текущее положение НКА ГЛОНАСС рассчитывается по оперативной ЭИ из НС методом Рунге-Кутта по уравнениям движения НКА, которые приведены в [1].

Согласованная эфемеридная информация и ПДМД НКА ГЛОНАСС, передаваемые в составе НС L1OC и L3OC, предназначены для расчета положения НКА на интервалах до 4 ч и включают в себя параметры вида x, y, z, x, y, z, x, y, z и a x 0 , a x 1 , a x 2 , a x3 , a x 4 , a y 0 , a y 1 , a y^ , a_Y3, a y 4 , a_Z 0 , a_Z 1 , a_Z 2 , a_Z3, a_Z 4 , заданные на опорное время t b .

Здесь x , y , z , x, y , z - составляющие векторов координат и скорости центра масс НКА ГЛОНАСС на опорную эпоху t b в СК ПЗ-90.11, x,y, z - составляющие вектора ускорения НКА в СК ПЗ-90.11, далее следуют 12 параметров долговременной модели движения.

Дополнительные ускорения НКА a_x ( t , t b ), a Y (t , t b ), a_z(t , t b ) на текущий момент времени t рассчитываются потребителем с использованием ПДМД, которые являются коэффициентами полиномов 4-й степени для разницы между текущим временем t и опорным временем t b , по алгоритмам, приведенным в [1]:

а у (t, th) — a + a у ,■ (t — th) + ay• ■ (t — th )2 + ay3- (t — th )3 + a • (t — th )4, X b X ° X i b X 2 b X 3 b X 4 b aY (t, tb) — aYо + aY, • (t — tb) + aY2 • (t — tb )2 + aY3 • (t — tb )3 + aY4 • (t — tb )4,

• " z ( tA . ) ^— a_z . + a zy (. — ₄ ) + a z , . ( , — t , )² + a z 3 • ( t ^— Ц )^{3 +} a z 4 <. — . ) )'

Задача построения согласованных эфемерид на опорные эпохи t b сводится к итерационному решению линеаризованной задачи:

• u — a.^, Au — 7|\у , .

Здесь A - вещественная матрица размерности m х n (матрица частных производных), и и *                                                                                                                                                    _                                                                                                                             *

f - векторы размерности n и m соответственно, и - уточняемый вектор состояния НКА, f -вектор правых частей (вектор невязок). Задача решается в условиях, когда входные данные {A, — f} возмущены.        _

Уточняемый вектор u включает в себя составляющие векторов скорости и ускорений НКА { x , y , z, x , y , z } , заданные в СК ПЗ-90.11 на опорную эпоху t b и ПДМД НКА ГЛОНАСС в составе а х о , a x i , а х2 , a x з , a x 4 , a Y о , a Y i , a_n , a Y з , a Y 4 , a z о , a z i , a z 2 , a z 3 , a z 4 . Параметры a x ° , a Y ° , a z о , передаваемые с борта НКА, предназначены для компенсации погрешности представления компонент ускорения x , y , z из-за усечения разрядности в НС L1OC, L3OC, и поэтому параметры a_{x о}, a_{Y о}, a_{z о} не требуется включать в состав уточняемого вектора. ^—

Уточнение вектора u проводилось в два этапа. На 1-м этапе на интервале согласования 0,5 ч [tb -о,25 ч ; tb +0,25 ч ] с использованием линеаризованной математической модели A ^_, — f , L b , b ,                                                   _                                                                         ¹     7¹

были получены оценки вектора состояния НКА и в составе { тс, y , z,x , y,z } (согласованные ско-¹

рости и ускорения).

Так как излучаемые в составе реального навигационного сообщения эфемериды недостаточно точны, в качестве опорной орбиты НКА были взяты точные эфемериды x(t b ), y(t b ), z(t b ), в расчетах использовали окончательные данные опорных эфемерид НКА с сайта СВОЭВП [2] на фиксированные опорные эпохи t b . Положение НКА на текущий момент времени t на интервале согласования рассчитывали при помощи интерполяционного многочлена Лагранжа 12-го порядка [3].

В общем случае вместо указанных данных могут быть использованы эфемериды НКА, спрогнозированные в инерциальной системе координат на требуемые моменты времени в полном поле сил, где ускорение НКА описывают вектором дифференциального уравнения rsat   ‘*Earth + aSun + aMoon + aSRP + ^^tides + aNGP t—Earth, где 3Earth - ускорения из-за несферичности Земли, рассчитываются по разложениям в ряд по

- - сферическим функциям не ниже восьмого порядка и степени включительно; aSun, aMoon - ускорения от солнечных и лунных гравитационных возмущений; aSRP - ускорения от сил радиаци-—

онного давления на корпус НКА (прямого и отраженного излучения Солнца); a tides – ускорения

^— из-за влияния лунно-солнечных приливных вариаций гравитационного поля Земли; a NGp -ускорения НКА от сил негравитационной природы, определяемые эмпирически. -

В качестве начального априорного значения уточняемого вектора состояния НКА u при расчетах на первой итерации были приняты составляющие вектора скорости и ускорения НКА в системе координат (СК) ПЗ-90.11 на опорную эпоху tb: x(tb), y(tb), z(tb), рассчитанные bbb при помощи интерполяционного многочлена Лагранжа [3] по значениям опорных эфемерид НКА ГЛОНАСС SP3 СВОЭВП x(tb), y(tb), z(tb), и составляющие вектора ускорений НКА x(tb),У(tb), z(tb) от солнечных и лунных гравитационных возмущений, рассчитанные по алгоритмам, приведенным в [1] (прил. К, У).                     -

Матрица частных производных A при уточнении вектора и 1 рассчитана методом конечных приращений, k – количество эпох на получасовом интервале, для которых рассчитаны частные

производные:
	( 8 x x )	( 8 x 1 )	( 8 x 1 )	( 8 x 1 )	( 8 X 1 )	( 8 x 1 )
	2( 8 x)	2( 8 y )	2( 8 z )	2( 8 Х ^)	2( 8 y )	2( 8 z )
	( 8 y J	( 8 У . )	( 8 y )	( 8 У 1 )	( 8 У 1 )	( 8 y J
Л —	2( 8 x)	2( 8 У )	2( 8 z )	2( 8 x )	2( 8 y )	2( 8 z )
	... ( 8 z з - )	... ( 8 z з k )	... ( 8 z 3 - ’	... ( 8 z з - )	( 8 z 3 k )	( 8 z 3 - )
	L 2( 8 x)	2( 8 y )	2( 8 z )	2( 8 Х ^)	2( 8 У )	2( 8 z ) _

При расчете частных производных приращения начальных условий скоростей и ускорений в программно-математической модели использовали приращения: |8x|,|8y|,|8z| ~ 10-7 км/с, 18x|, 8У, |8z| ~ 10—6 км/с. Каждые три элемента столбца матрицы A на моменты времени ti (на- пример,

( 8 x , -) ( 8 y , -) ( 5 z^ 2( 8 y ),2( 8 y /2( 8 у )

определяют по результатам интегрирования уравнений движе-

ния НКА на моменты времени t i по алгоритму расчета К.2.1 [1] при возмущении начальных условий соответствующего уточняемого элемента с положительным и отрицательным прира- - 7                             - 7

щением (в данном случае при значениях 8 y ( t_b ) = + 10 км/с и S y ( t b ) = - 10 км/с ).

_         ^-

Систему условных уравнений Au 1 = / 1 на каждой итерации решали с применением классического МНК. Для повышения численной устойчивости решения задачи предварительно было проведено масштабирование столбцов матрицы A с тем, чтобы все элементы матрицы частных производных A находились в диапазоне: | a j | < 1.

Чтобы процедура масштабирования не вносила дополнительные погрешности в исходные данные {A, f}, масштабирующий множитель целесообразно брать равным 10-n, где для каждого столбца матрицы A параметр n е N определяется из условия 10n ~ max |aj. Оценка числа обусловленности cond(A) = ||A||-|A-1 , проведенная с использованием сингулярного разложения по алгоритмам [4, 5], показала, что предлагаемая процедура масштабирования позволяет понизить число обусловленности матрицы условных уравнений A с 360 до 1,3 и повысить чис- ленную устойчивость данной задачи, а также снизить погрешности определения оцениваемого вектора при нахождении решения системы уравнений.

Для решения системы уравнений A T Au_v = A T f использовали алгоритм экономного пере- 1

счета треугольных сомножителей метода Холецкого (метод квадратного корня), приведенный в [5, 6]. Сходимость итерационной последовательности оценки вектора состояния НКА {х(tb), y(tb), z(tb), х(tb), y(tb), z(tb)} зависит от начального априорного значения вектора, однако систему уравнений требуется решать не более двух-трех раз благодаря быстрой сходимости метода Ньютона. Критерием сходимости являлись значения поправок к уточняемому вектору {Дtb),У(tb),z(tb),^(tb),У(tb),z(tb)} на текущей итерации, не превышающие по абсолютному значению цену младшего разряда их представления в навигационной цифровой информации, а именно величин ±0,001 мм/с и ±2 • 10-6 мм/с2 по компонентам скорости и ускорений НКА соответственно, а критерием успешного решения задачи считали эквивалентные по точности решения, обеспечивающие расчет положения НКА со среднеквадратическим отклонением (СКО) от опорных эфемерид СВОЭВП на 15-минутном интервале на уровне, втрое меньшем, чем уровень погрешности, заданный в Таблице К.1 [1] для упрощенного алгоритма, т.е. не более 1,6 см.

По согласованной (в части скоростей и ускорений) ЭИ НКА проведен расчет положения НКА на интервале согласования 0,5 ч [ t b -0,25 ч ; t b +0,25 ч ] и апостериорная оценка погрешности расчета положения НКА относительно опорных эфемерид SP3 СВОЭВП. Результаты оценок приведены ниже.                                                      *

На 2-м этапе на интервале согласования 4 часа [t_b ; к +4 ч ] был уточнен вектор и , в составе b b                                 2

{ a_X1 , a_X2 , a X 3 , a_X 4 , a Y i , a Y ₂, a Y ₃, a_{Y 4}, a Z i , a Z ₂, a Z ₃, a Z 4 }. В качестве начальных условий использовали окончательные данные опорных эфемерид НКА x(t b ), y(t b ), z(t b ) с сайта СВОЭВП на фиксированные опорные эпохи t b и согласованные скорости и ускорения на опорные эпохи t b , полученные на первом этапе.                                                     *

В качестве начального априорного значения уточняемого вектора u могут быть приняты нулевые значения параметров { a_X 1 , a X2 , a X3 , a_{X 4}, a Y 1 , a Y ₂, a_{Y 3}, a Y ₄, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} или любые значения из диапазона приращений начальных условий, используемых при расчете матрицы частных производных. *

Матрица частных производных A при уточнении вектора и ₂ рассчитана методом конечных приращений. При расчете частных производных приращения начальных условий для вектора { a X , a_X2 , a_X3 , a_{X 4}, a Y 1 , a_Y2 , a_Y3 , a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} в программно-математической модели использовали значения приращений соответственно для \5а _х J,| S a_Y J, \5a _z J ~5 • 10^-14 км/с ³, для I S a x 2I, l ^ a r 2I, V a Z_Z 2I ~ ⁵ • ^{10 А км/с 4} , для l ^ a X 3 |, l ^ a F 3 I, V a^<Z_Z з| ~ ⁵ • ¹⁰ "^{22 км/с 5} , для l ^ a X 4I, | ^ ^aF 4I, l ^ a z 4 ~5 • 10^-27 км/с ⁶. Приращения могут быть выбраны иными, однако они должны выбираться из диапазона устойчивой области зависимости производных от приращений на одной тестовой эпохе при интегрировании на +4 ч. Здесь k - количество эпох на 4-часовом интервале, для которых рассчитывают частные производные.

Анализ показал, что масштабирование матрицы A позволяет значительно понизить число обусловленности - с 6 • 10¹³ до 2,5 • 10³. Однако для данного состава уточняемых параметров, несмотря на понижение числа обусловленности, матрица системы уравнений все еще является плохо обусловленной и относительная погрешность решения может возрасти примерно в

2500 раз по сравнению с погрешностью расчета правой части при решении системы уравнений Au = f . ^*

По смыслу постановки задачи все допустимые решения задачи АЙ = f должны являться эквивалентными по точности решениями этой системы уравнений. Тестовые расчеты показа- ли, что при использовании классического МНК для оценки вектора и в составе {axb ax2, aX3, ax4, aY 1, aY2, aY3, aY4, az 1, az2, az3, az4} решения от итерации к итерации могут существенно раз— личаться и зависят от задания начальных априорных значений уточняемого вектора и.

Согласно [7, 8], такие задачи относятся к классу некорректных. В условиях, когда входные данные {A, f} возмущены, матрица A является плохо обусловленной, для отыскания устойчи вых приближений к элементу uf, uf = argmin||u||B широко применяется метод регуляризации uAu=f

• [7,8].    При этом B = B T > 0, A T A + B > о, M B = ⁽ Bu , u Г.    ^

Регуляризованное решение системы уравнений Au = f находится как

• ^u “ =^arg^min(|| Au — f II₂²+ « -\ l u ll Л u

Элемент u^a определяется из уравнения

(AT A + aB)u = AT f, где a > 0 – параметр регуляризации.

При оценке вектора { a X , a_x2 , a_x3 , a X ₄, a Y ₁, a_Y2 , a Y ₃, a Y ₄, a Z ₁, a Z ₂, a Z ₃, a Z ₄} был применен эвристический (прагматический) выбор параметра регуляризации с уменьшением значения параметра регуляризации от итерации к итерации по принципу невязки.

Априорная B матрица имеет смысл ковариационной матрицы случайных ошибок уточняемого вектора { a xi , a x2 , a x3 , a x 4 , a Y 1 , a y 2 , a Y 3 , a Y 4 , a z 1 , a z 2 , a z 3 , a z 4 } и в начале каждой итерации полагалась диагональной.

Для повышения численной устойчивости процесса при решении уравнений ( A T A + aB ) u = A T f был применен метод Холецкого.

Сходимость итерационной последовательности оценки вектора состояния НКА { a_{x 1}, a_{x 2}, a_x3 , a_{x 4}, a_{Y 1}, a_{Y 2}, a_{Y 3}, a_{Y 4}, a_{z 1}, a_{z 2}, a_{z 3}, a_{z 4}} зависит от начального априорного значения вектора, однако систему уравнений требуется решать не более трех-четырех раз. Критерием сходимости являлись значения поправок к уточняемому вектору { a_{x 1}, a_x2 , a_x3 , a_{x 4}, a_{Y 1}, a_{Y 2}, a_{Y 3}, a_{Y 4}, a_{z 1}, a_{z 2}, a_{z 3}, a_{z 4}} на текущей итерации, не превышающие по абсолютному значению цену младшего разряда их представления в навигационной цифровой информации, а именно величин: ±5 • 10^-17 км/с ³ для { a_{x 1}, a_{Y 1}, a_{z 1}}, ±6 • 10^-21 км/с ⁴ для { a_{x 2}, a_{Y 2}, a_{z 2}}, ±8 • 10^-25 км/с ⁵ для { a_x3 , a_{Y 3}, a_{z 3}}, ±2 • 10^-29 км/с ⁶ для { a_{x 4}, a_{Y 4}, a_{z 4}}, а критерием успешного решения задачи считали эквивалентные по точности решения, обеспечивающие расчет положения НКА с СКО от опорных эфемерид СВОЭВП на четырехчасовом интервале на уровне, втрое меньшем, чем уровень погрешности, заданный в Таблице К.1 [1] для долговременного алгоритма, т.е. не более 33,3 см.

По согласованной (в части скоростей и ускорений) ЭИ НКА и с использованием уточненных ПДМД проведен расчет положения НКА на интервале согласования [tb; tb +4 ч] и апосте-– 794 – риорная оценка погрешности расчета положения НКА относительно опорных эфемерид SP3 СВОЭВП. Результаты оценок приведены ниже.

Апостериорная оценка погрешности расчета положения НКА

Предложенные методы определения вектора согласованных эфемерид и ПДМД были протестированы для НКА ОГ ГЛОНАСС для получасовых и четырехчасовых интервалов согласования за даты с 18.12.2016 по 21.12.2016.

На первом этапе были получены оценки скоростей и ускорений НКА на неперекрываю-щихся получасовых интервалах согласования [t_b -0,25 ч ; t b +0,25 ч ] для опорных эпох t b на 15-ю и 45-ю минуты часа.

Частные производные при оценке вектора { x, y, z, x, y, z } рассчитывали с шагом 5 с. Оценки отклонений положения НКА (евклидово расстояние) по согласованным эфемеридам НКА от опорных эфемерид SP3 СВОЭВП рассчитывали с шагом 1 с.

Среднеквадратические отклонения положений НКА, рассчитанных на интервале [ t b -0,25 ч ; t b +0,25 ч ] по согласованной (в части скоростей и ускорений) ЭИ НКА, от опорных эфемерид SP3 СВОЭВП изображены на рис. 1.

По результатам, приведенным на рис. 1, можно видеть, что погрешность расчета положения НКА (СКО) по согласованным в части скоростей и ускорений эфемеридам на 15-минутном

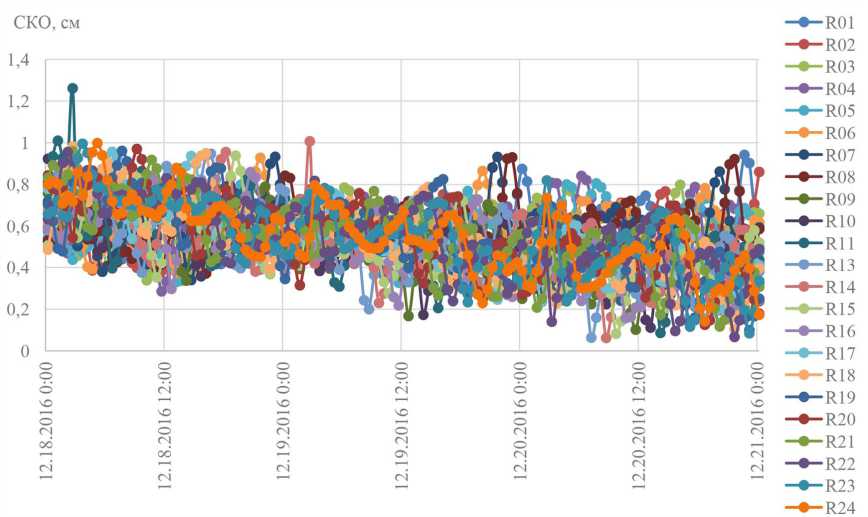
Рис. 1. Погрешности расчета положения НКА (СКО) по согласованной в части скоростей и ускорений ЭИ НКА ОГ ГЛОНАСС на интервалах согласования [ t b -0,25 ч ; t b +0,25 ч ]

Fig. 1. GLONASS SV (R01 ... R24) Position accuracy (standard deviations) after forecast in accordance with User Algorithm K.2.1 for Determination of SV Position [1]. Improved Ephemeris data sets {. f ( t b ), y ( t b ), z(t b ), x ( t b ), y(t b ), z ( t b ) } are produced via a least squares curve fit of the SP3 SVOEVP ephemeris, fitting intervals are [ t b -0,25 ч ; t b +0,25 ч ]). The values of SV Position parameters { x ( t b ), y ( t b ), z(t b )} match with SP3 SVOEVP ephemeris

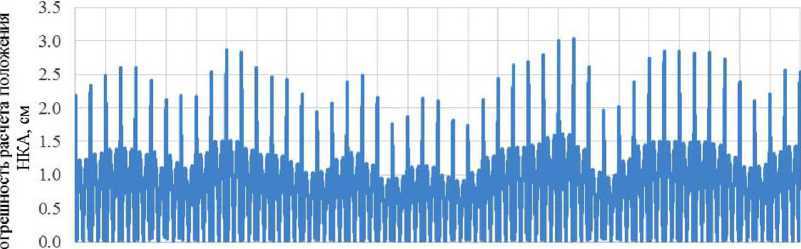
С   оооооооооооооооооооооооо ppppoqqppppppppppppppppp

— г> гл Tt ^ ,з г- и 3i о — г> гл м- ^, .с г- ос О', о — ел гл о

Рис. 2. Оценка погрешности расчета положения НКА (невязки) по согласованным эфемеридам для НКА ГЛОНАСС №730, системная точка 1, дата 18.12.2016, состав уточняемого вектора { ^Х( t b X y ⁽ t b X ^Z( t b X x ⁽ t b ), ^y( t b ), z⁽ t b ) }

Fig. 2. Deviations of the calculated GLONASS SV R01 Positions from the exact SP3 SVOEVP ephemeris (December 18, 2016) after forecast on intervals [tb; tb +0,25 ч] in accordance with User Algorithm K.2.1 for Determination of SV Position [1]. Ephemeris data sets f {x(tb),y(tb),Z(tb),x(tb),y(tb),Z(tb)} are produced via a least squares curve fit of the SP3 SVOEVP ephemeris, the values of SV Position parameters {x(tb), y(tb), z(tb)} match with SP3 SVOEVP ephemeris интервале от опорной эпохи tb не превысила 1 см, за исключением двух реализаций из 3480, которые составили 1,26 и 1,01 см. Следовательно, согласованная эфемеридная информация НКА ГЛОНАСС позволит обеспечить требование [1] по точности расчета положения НКА с погрешностью не более 5 см на всем получасовом интервале согласования.

На рис. 2 приведены результаты оценки погрешности отклонения положения НКА (невязки) по согласованным эфемеридам для НКА ГЛОНАСС №730, системная точка 1, дата 18.12.2016, в качестве эталонных эфемерид использованы опорные эфемериды SP3 СВОЭВП. Интервалы расчета положения НКА для каждой опорной эпохи tb: [tb -0,25 ч; tb +0,25 ч], состав уточняемого вектора {x(tb), y(tb), Z(tb), x(tb), y (tb), Z(tb)}. Погрешность расчета положения НКА по согласованным эфемеридам (в части скоростей и ускорений) составила не более 3 см на 15-минутном интервале от момента t . Сопоставимые по точности расчета положения НКА b результаты получены по другим НКА ГЛОНАСС.

Тестовые расчеты показали, что если на опорные эпохи t_b используются окончательные опорные эфемериды SP3 СВОЭВП и скорости, полученные интерполяцией эфемерид SP3 СВО-ЭВП на соответствующие опорные эпохи t b , а в состав уточняемого вектора входят только ускорения НКА x ( t b ), y ( t b ), Z ( t b ), погрешность расчета положения НКА по алгоритму потребителя [1] на 15 минутном интервале в большей части реализаций превышает 5 см, т.е. требование [1] по точности расчета положения НКА по согласованной ЭИ не удовлетворяется.

На рис. 3 отражены результаты оценки отклонения расчетного положения НКА ГЛОНАСС №730 по согласованной (только в части ускорений) ЭИ, системная точка 1, дата 18.12.2016, в качестве эталонных использованы опорные эфемериды СВОЭВП и компоненты скорости, рассчитанные при помощи интерполяционного многочлена Лагранжа 12-го порядка. Интервалы расчета положения НКА для каждой опорной эпохи t_b : [ t_b -0,25 ч ; t_b +0,25 ч ], состав уточняемого вектора { x ( t b ), y ( t b ), Z ( t b ) } . Погрешность расчета положения НКА только для двух реализа-

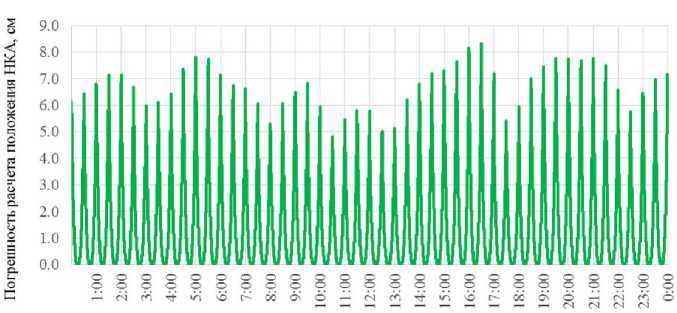
Рис. 3. Оценка погрешности расчета положения НКА по согласованной (только в части ускорений) ЭИ для НКА ГЛОНАСС №730, системная точка 1, дата 18.12.2016, состав уточняемого вектора { % ( t b ), y(t b ), z(t b ) } (координаты и скорости НКА на моменты t_b соответствуют опорным эфемеридам SP3)

на интервалах интегрирования до 15 мин от опорной эпохи t_b составила до 6…8 см.

Таким образом, с точки зрения обеспечения требования [1] по точности расчета положения НКА ГЛОНАСС вариант формирования согласованной ЭИ на интервале [ t b -0,25 ч ; t b +0,25 ч ], когда в состав уточняемого вектора включены как компоненты скорости, так и компоненты ускорения НКА, а в качестве координат НКА используются опорные эфемериды SP3 на момент t b , предпочтительнее.

Исключение из состава уточняемого вектора компонент скоростей и замена уточненных компонент скорости НКА { x ( t b ), y ( t b ), z ( t b ) } на компоненты скорости, полученные интерполированием опорных эфемерид SP3, приводит к увеличению погрешности расчета положения НКА на интервале [ t b -0,25 ч ; t b +0,25 ч ] до 2.. .3 раз.

На 2-м этапе были получены оценки погрешности расчета положения НКА на основе согласованной ЭИ и уточненных ПДМД для опорных эпох t b на 15-ю и 45-ю минуты часа на интервалах согласования [ t b ; t b +4 ч ]. Задача решалась итерационным методом Ньютона с использованием устойчивых регуляризирующих алгоритмов по А.Н. Тихонову [7, 8], описанных выше. При оценке вектора { a_n , a_{x 2}, am , ax 4, a y 1, a y2, a y3, a y4, a_z 1, az 2, am , az 4} частные производные на интервале согласования 4 ч рассчитывали с шагом 60 с, при интегрировании уравнений движения НКА ГЛОНАСС использовали долговременный алгоритм [1].

Для оценки устойчивости решения задачи были проведены расчеты с различными начальными априорными значениями вектора { a X1 , a X2 , a X3 , a_X 4 , a Y 1 , a_{Y 2}, a_{Y 3}, a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_Z 4 } - с нулевыми значениями и с возмущенными, ненулевыми значениями на уровне ~5 • 10^-14 км/с ³ для | a_X /⁰⁾| , | a_Y 1⁽⁰⁾| , | a_Z /⁰⁾ , ~5 • 10^-18 км/с ⁴ для | a_{X 2}⁽⁰⁾|, | a_{Y 2}⁽⁰⁾|, | a_{Z 2} ⁽⁰⁾ , ~5 • 10^-22 км/с ⁵ для ^ 1,3 ₃⁽⁰⁾| , \ a_{Y 3}⁽⁰⁾| , \ a_{z 3} ⁽⁰⁾ , ~5 • 10^-27 км/с ⁶ для | a_{X 4}⁽⁰⁾| , \ a_{Y 4}⁽⁰⁾| , \ a_{z 4} ⁽⁰⁾ .

Расчет отклонений положения НКА, рассчитанной по согласованной ЭИ и ПДМД НКА, от положения НКА, рассчитанного по опорным эфемеридам SP3 СВОЭВП по интерполяционным полиномам Лагранжа, производили с шагом 1 с.

Для оценки эффективности использования метода регуляризации был также реализован вариант определения вектора { a X 1 , a_{X 2}, a X 3 , a_{X 4}, a_Y 1 , a_{Y 2}, a Y 3 , a_{Y 4}, a Z i , a_{Z 2}, a_{Z 3}, a_Z 4 } с использованием классического МНК. При использовании указанного метода при оценке вектора { a_X 1 , a_X2 , a X3 , a X ₄, a_Y 1 , a Y ₂, a Y ₃, a Y4 , a Z 1 , a Z ₂, a Z ₃, a Z ₄} для части реализаций возможно получить решения системы уравнений, сопоставимые с теми, которые были получены с применением регуляри-зирующих алгоритмов – погрешность расчета положения НКА на интервале согласования 4 ч может не превышать 0,10…0,25 м.

Однако процесс решения системы условных уравнений с применением классического МНК, а не регуляризирующих алгоритмов является неустойчивым. Конечные результаты оценки вектора { a_X 1 , a_X2 , a_X3 , a_{X 4}, a_Y 1 , a_{Y 2}, a_{Y 3}, a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} с использованием классического МНК зависят от уровня возмущения начального априорного значения уточняемого вектора, критерий сходимости для прекращения итерационного уточнения вектора ПДМД для части реализаций может быть не выполнен. Тестовые расчеты показали, что погрешность расчета положения НКА на интервале согласования 4 ч относительно опорных эфемерид SP3 СВОЭВП может достигать 25 м и более, если применены ПДМД, уточненные с использованием классического МНК.

Таким образом, в случае применения классического МНК не все реализации уточнения вектора { a_X 1 , a_X2 , a_X3 , a_{X 4}, a_Y 1 , a_Y2 , a_{Y 3}, a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} обеспечивают эквивалентные по точности расчеты положения НКА на интервале согласования, а для ряда реализаций уточнения указанного вектора не выполняется требование [1] по точности.

В качестве примера на рис. 4 приведены результаты оценки погрешности расчета положения НКА для варианта применения классического МНК без регуляризации для уточнения вектора { a_X 1 , a X 2 , a X 3 , a_{X 4}, a_Y 1 , a_Y2 , a_{Y 3}, a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} с нулевыми и возмущенными значениями, задаваемыми в качестве начального априорного значения вектора.

Апостериорные оценки погрешности расчета положения НКА показали, что при применении регуляризирующих алгоритмов по А.Н. Тихонову для всех реализаций решения задачи обеспечиваются эквивалентные точности вне зависимости от того, заданы ли начальные априорные значения вектора { a_X 1 , a_{X 2}, a_X3 , a_{X 4}, a_Y 1 , a_{Y 2}, a_Y3 , a_{Y 4}, a_Z 1 , a_{Z 2}, a_{Z 3}, a_{Z 4}} до начала уточнения нулевыми или возмущенными.

На рис. 5, 6 приведены результаты оценки точности расчета положения НКА по согласованной (в части скоростей и ускорений) ЭИ и ПДМД - соответственно среднеквадратические отклонения (СКО) и абсолютные отклонения положения НКА ОГ ГЛОНАСС от опорных эфемерид SP3 СВОЭВП (невязки) при расчете положения НКА на интервалах согласования [t b ; t b +4 ч ] для варианта, в котором для определения вектора { a_X 1 , a X ₂, a X ₃, a_{X 4}, a_Y 1 , a_{Y 2}, a Y3 , a_{Y 4}, a_Z 1 , a Z ₂, a Z ₃, a Z ₄} использованы устойчивые регуляризирующие алгоритмы по А.Н. Тихонову.

Погрешность расчета положения НКА (СКО) в интервалах до 4 ч от опорной эпохи t_b по алгоритмам ИКД по согласованной эфемеридной информации в части параметров { a X 1 , a_X2 , a_{X 3}, a_{X 4}, a_{Y i}, a_{Y 2}, a_{Y 3}, a_{Y 4}, a_{Z i}, a_{Z 2}, a_{Z 3}, a_{Z 4}} для рассматриваемого интервала моделирования не превысила 6 см, при этом для более 95 % реализаций обеспечивался расчет положения НКА – 798 –

-•- GLO-02_CKO_MHK ПДМД НУ нулевые

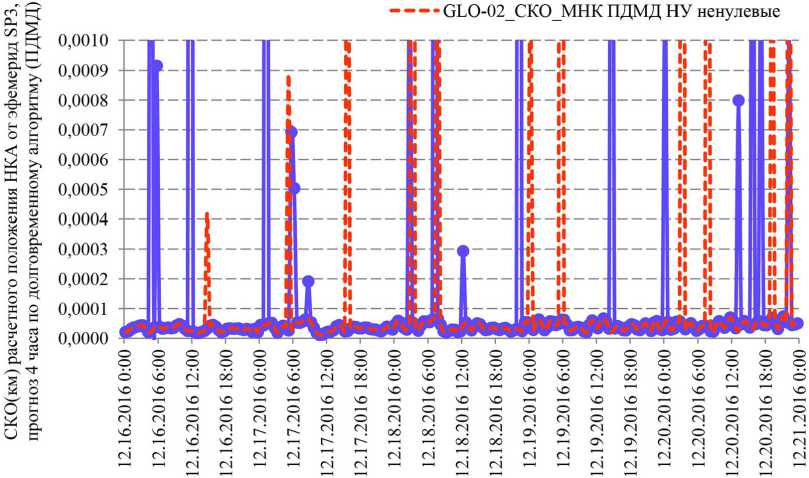
Рис. 4. Оценка погрешности расчета положения НКА (СКО) на интервалах [t b , ; t b +4 ч ] по согласованной ЭИ для НКА ГЛОНАСС №747, системная точка 2, даты 16.12.2016 - 20.12.2016, состав уточняемого вектора { a X 1 , a_{X 2} , a_{X 3} , a_X 4 , a_Yb a_Y2 , a_Y3 , a_{Y 4} , aZ_b a_{Z 2} , a_{Z 3} , a_{Z 4} }, применен классический МНК, без регуляризации

Все реализации расчета положения НКА по согласованной в части скоростей и ускорений ЭИ и ПДМД { a_X ь a X ₂, a X ₃, a X ₄, a_Y ь a_{Y 2}, a_{Y 3}, a_{Y 4}, a_Z ь a Z ₂, a Z ₃, a Z ₄}, рассчитанных с использованием регуляризирующих алгоритмов по А.Н. Тихонову, эквивалентны по точности и обеспечили расчет положения НКА на интервалах [ t b ; t b +4 ч ] с погрешностью, не превышающей 0,2 м.

Исходя из вышеизложенного можно сделать вывод, что верхняя граница требования [1] по погрешности расчета положения НКА по долговременному алгоритму не более 1 м на интервалах расчета положения НКА до +4 ч от опорной эпохи t_b обеспечивается с запасом.

Заключение

В данной работе представлены способы оценки вектора { х ( t b ), y ( t b ), z ( t b ), х ( t b ), y(t b ), z ( t b ) } НКА ГЛОНАСС и вектора параметров долговременной модели движения НКА ГЛОНАСС { a_{X 1}, a_{X 2}, a X ₃, a X 4 , a_{Y 1}, a_{Y 2}, a_{Y 3}, a_Y 4 , a Z ₁, a Z ₂, a Z ₃, a Z ₄}, обеспечивающих расчет параметров движения НКА ГЛОНАСС по алгоритмам [1] с высокой точностью на интервалах согласования соответственно до ±15 мин и до +4 ч от опорной эпохи t b .

Показано, что параметры движения НКА ГЛОНАСС в составе опорных эфемерид НКА ГЛОНАСС SP3 СВОЭВП x ( t b ), y(t b ), z(t_b ), скоростей и ускорений НКА { i r( t b ), y ( t b ), z ( t b ), x ( t b ), _ y ( t b ), z ( t b ) } ,

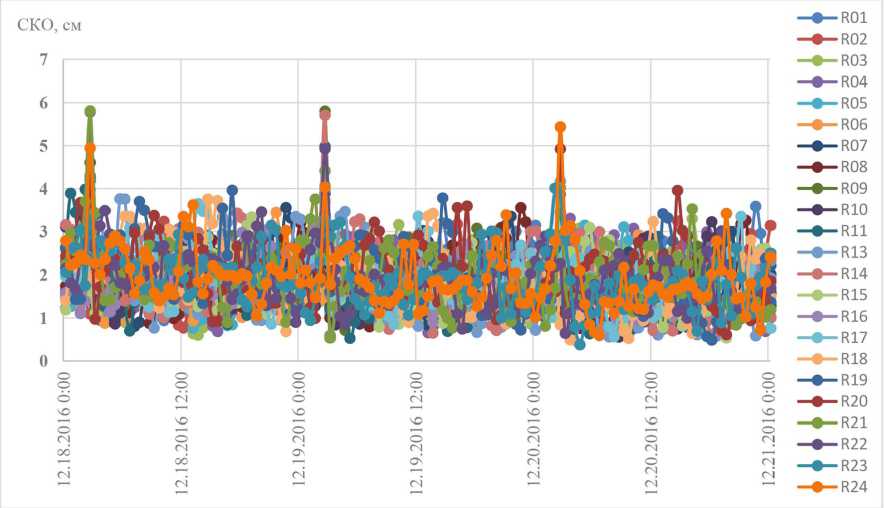
Рис. 5. Оценка погрешности расчета положения НКА (СКО) на интервалах [ t b ; t b +4 ч ] по согласованной ЭИ и ПДМД для НКА ОГ ГЛОНАСС, даты 18.12.2016 – 20.12.2016. ЭИ НКА ОГ ГЛОНАСС согласована в части скоростей и ускорений. Состав уточняемого вектора ПДМД { a_{X 1} , a_{X 2} , a_{X 3} , a_{X 4} , a_{Y 1} , a_{Y 2} , a_{Y 3} , a_{Y 4} , a_{Z 1} , a Z 2 , a Z 3 , a Z 4 }, применен метод регуляризации по А.Н. Тихонову

Fig. 5. GLONASS SVs (R01 … R24) Position accuracy (standard deviations) after forecast on intervals [ t b ; t b +4 ч ] in accordance with User Algorithm K.3.1 for Determination of SV Position [1], December 16 – December 18, 2016. The Long-term model parameter sets { a X 1 , a X 2 , a X 3 , a X 4 , a Y 1 , a Y 2 , a Y 3 , a Y 4 , a Z 1 , a Z 2 , a Z 3 , a Z 4 } for L1OC, L3OC navigation message are produced via A. N. Tikhonov regularizing method curve fit of the SP3 SVOEVP ephemeris, fitting intervals are [ t b ; t b +4 ч ]

уточненных на интервале [ t b –0,25 ч ; t b +0,25 ч ], и ПДМД НКА { a X 1 , a X 2 , a X 3 , a X 4 , a Y 1 , a Y 2 , a Y 3 , a Y 4 , a Z 1 , a Z 2 , a Z 3 , a Z 4 }, уточненных на интервалах [ t b ; t b +4 ч ] с применением регуляризирующего алгоритма А.Н. Тихонова, позволяют обеспечить расчет положения НКА по алгоритмам [1] с погрешностью не более единиц дециметров на интервалах согласования до 4 ч – в тестовых расчетах погрешность расчета положения НКА ОГ ГЛОНАСС не превысила 0,2 м.

Оценена эффективность применения регуляризирующего алгоритма А.Н. Тихонова по сравнению с результатами, полученными при использовании классического МНК.

Следует отметить, что решения для вектора { a X 1 , a X 2 , a X 3 , a X 4 , a Y 1 , a Y 2 , a Y 3 , a Y 4 , a Z 1 , a Z 2 , a Z 3 , a_{Z 4}}, полученные с использованием классического МНК, неустойчивы, результаты оценки вышеуказанного вектора существенно зависят от начальных априорных значений уточняемых параметров и не гарантируют точность расчета параметров движения НКА, эквивалентных по точности решениям по регуляризирующему алгоритму. Погрешности расчета положения НКА с ПДМД, уточненными по классическому МНК, относительно эталонных эфемерид SP3 СВОЭВП (евклидово расстояние) на интервалах до +4 ч от опорной эпохи t b для некоторых реализаций уточнения ПДМД могут достигать 20 м … 25 м.

Представленный выше метод определения ПДМД НКА ГЛОНАСС { a X 1 , a X 2 , a X 3 , a X 4 , a Y 1 , a Y 2 , a Y 3 , a Y 4 , a Z 1 , a Z 2 , a Z 3 , a Z 4 } с использованием регуляризирующего алгоритма А.Н. Тихонова может быть применен в программном обеспечении генерации навигационной цифровой ин- – 800 –

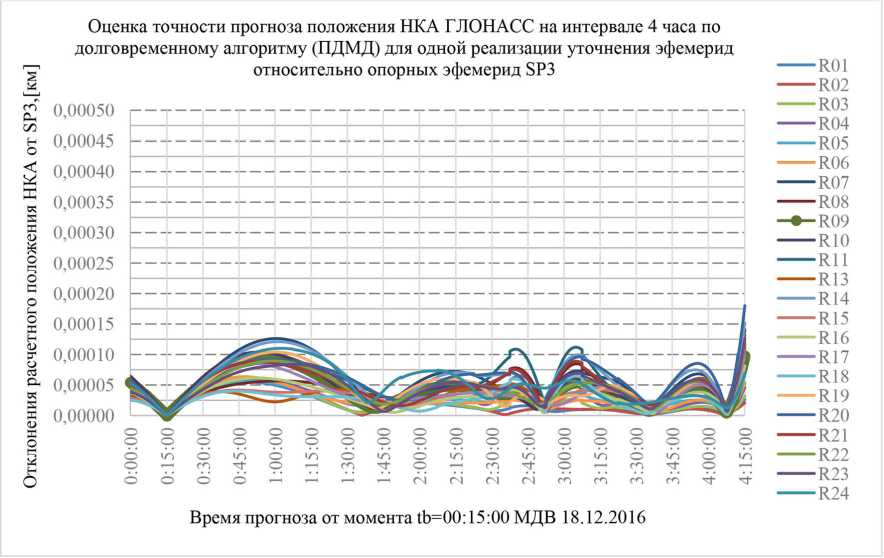
Рис. 6. Оценка погрешности расчета положения НКА (невязки) на интервале [ t b ; t b +4 ч ] по согласованной ЭИ и ПДМД для НКА ОГ ГЛОНАСС, дата 18.12.2016, t b 00:15:00 МДВ. ЭИ НКА ОГ ГЛОНАСС согласована в части скоростей и ускорений. Состав уточняемого вектора ПДМД { a X 1 , a X 2 , a X 3 , a X 4 , a Y 1 , a Y 2 , a Y 3 , a Y 4 , a , a , a , a }, применен метод регуляризации по А.Н. Тихонову

Fig. 6. Deviations of the calculated GLONASS SV (R01 … R24) Positions from the exact SP3 SVOEVP ephemeris (December 18, 2016) after forecast on intervals [tb; tb +4 ч] in accordance with User Algorithm K.3.1 for Determination of SV Position [1]. Ephemeris data sets for L1OC, L3OC navigation message are used: the values of SV Position parameters {x(tb), y(tb), z(tb)} match with SP3 SVOEVP ephemeris; improved data sets {i(tb),y(tb), z(tb), x(tb),y(tb), z(tb)} are produced via a least squares curve fit of the SP3 SVOEVP ephemeris; the Long-term model parameter sets {aX1, aX2, aX3, aX4, aY1, aY2, aY3, aY4, aZ1, aZ2, aZ3, aZ4} are produced via A.N. Tikhonov regularizing method curve fit of the SP3 SVOEVP ephemeris формации L1OC, L3OC ГЛОНАСС, предназначенной для тестирования навигационных приемников с целью оценки погрешности алгоритмов определения местоположения.

Указанный метод устойчивого определения ПДМД может быть также применен в программном обеспечении НКА «Глонасс-К2» при формировании навигационной цифровой информации L1OC, L3OC ГЛОНАСС на борту НКА.