О «справедливой» оценке долей инвестора и разработчиков в стартап-компании

В современном мире новые идеи в значительно большей степени, чем сбережения и инвестиции, являются ключом к процветанию. Новые идеи в бизнесе могут приносить больший вклад в увеличение прибыли и процветание компании, чем инвестиции. В результате появления и развития «креативных технологий» резко ограничивается значение финансов с точки зрения конкурентной экспансии. Деньги перестают быть главным источником рыночной силы, а становятся всего лишь одним из необходимых экономических ресурсов этой силы, они теряют значение первостепенности, так как конкуренция все больше определяется наличием уникальных технологий.

На увеличение стоимости стартап-компании в период её роста работают не только и не столько деньги инвестора, сколько инновационная идея, креативность изобретателей, готовность разработчиков действовать в условиях неопределённости и риска, их управленческая и уникальная инно-ваторская активность. Все это необходимо учитывать при построении моделей для оценки распределения долей между инвестором и разработчика- ми.

Классическая формула для определения доли инвестора (см., например, [1, 2]) имеет следующий вид:

S =

I

I + V pre

-money

где S — доля инвестора, I — его инвестиции в компанию, V p_{re - mone}y — стоимость компании до инвестирования.

На практике инвестиции не осуществляются единовременно, а поступают последовательными порциями в течение некоторого, иногда весьма продолжительного, промежутка времени. В формуле (1) это обстоятельство можно учитывать двумя способами — без дисконтирования, то есть без приведения разновременных инвестиций к началь- ному моменту времени, либо с дисконтированием. Первая из нижеприведённых формул определяет инвестиции в случае отсутствия дисконтирования, вторая — с учётом дисконтирования:

NN

I = E I n , I У , (2) n =1 n =1 ^V '

где I _n — инвестиции в момент времени n ; r — коэффициент дисконтирования; N — длина промежутка инвестирования; время дискретно, n = 1 , 2 , ...

Поясним основную идею настоящей работы. В формуле (1), определяющей долю инвестора, знаменатель трактуется как итоговая стоимость компании. Однако такая оценка, на наш взгляд, не учитывает должным образом инноваторскую деятельность разработчиков. В результате стоимость компании оказывается заметно заниженной, следствием чего является завышение доли инвестора и соответственно занижение доли разработчиков.

В работе строится и анализируется математическая модель «справедливого» распределения долей инвестора и разработчиков.

II.    Математическая модель

Для дальнейших рассуждений нам дополнительно потребуются следующие обозначения: V _n — стоимость компании в момент времени n без учёта инвестиций в этот момент времени; K _n — капитал, принадлежащий инвестору в момент n , включая инвестиции, сделанные им в этот же момент; S _n — доля инвестора в момент n с учётом сделанных в этот момент инвестиций; I _n — инвестиции в момент n = 1 , 2 , ...

В сделанных обозначениях V 1 имеет смысл начальной стоимости компании до инвестиций в нее, то есть это сумма, на которую был оценен исходный стартап.

После того как в момент n = 1 в компанию вложили инвестиции в размере 11, её стоимость мгновенно механически возросла и стала равной V1 +11. Чему при этом будет равна стоимость компании в момент n = 2? Как мы увидим в дальнейшем, от ответа на этот вопрос существенно зависит распределение долей инвестора и разработчиков. Заметим, что в варианте классической формулы (1), не учитывающем дисконтирование, считается, что стоимость компании в момент n = 2 равна V1 +I1. Однако на самом деле реальная стоимость компании в момент времени n = 2 составит V2 = (V1 + I1) а, где а — коэффициент, который показывает, насколько хорошо сработали разработчики-инноваторы, получив инвестиции: реализовали свою модель, разработали новые версии продукта, проработали многочисленные нюансы, детали и т. п. Далее в работе для простоты считается, что коэффициент α постоянен.

Применив аналогичные рассуждения ко второму и последующим моментам времени, получим следующую формулу для описания стоимости компании в произвольный момент n :

V n = ( V n- 1 + I n- 1 ) а =

у--- "- 1---⁽ V n- ^{1 +} I n

V n- 1 + I n- 1

1 ) а + I n = K n- 1 а + I n ,

n = 2 , 3 , ..., из которого легко получается формула, выражающая капитал инвестора через его инвестиции:

K n = K n- 1 а + I n = ( K n- 2 а + I n- 1 ) а + I n =

= ... = 1 1 а "^{- 1} + 1 2 а "^{- 2} + ... + I n = ^E I i " n-i - (6)

i =1

Итогом этих выкладок является окончательная формула, определяющая долю инвестора через его инвестиции и начальную стоимость компании:

S n

K n

^V n ⁺ I n

n

E I i а "

______ i =1 _______________

V 1 " "- ¹ + ^E I ' " "^-'

i =1

n = 1 , 2 , ...

III. Сравнение с классическим

n- 1

= V n— 1 а + I n— 1 а = V l а "^{- 1} + E I i а "^- ,   (3)

i =1

n = 2 , 3 , ... Перейдём к выводу формулы, описывающей долю инвестора в компании. Далее стоимость принадлежащей инвестору части компании будем называть его капиталом. Доля инвестора определяется как отношение его капитала к стоимости компании. В момент времени n = 1 капитал инвестора равен инвестициям, сделанным им в первом периоде: K 1 = I 1 . Соответственно его доля в этот момент составляет

подходом

Из (1) и (2) получаем два часто используемых классических определения доли инвестора. Первое определение относится к случаю отсутствия дисконтирования, второе — к случаю учёта дисконтирования:

,₌    E n =i I i

(E n =i I i + v i ) ’

V "  I i i =1 (1+ r ) i ^{- 1}

(E " =1(1+ Г - + V i )

S 1 =

K 1

V l + 1 1 .

Доля инвестора не меняется до следующей инвестиции, поэтому капитал инвестора в момент времени n = 2 по определению будет равен K 2 = S 1 V > + I 2 . Получив значение капитала, можно определить долю инвестора в этот момент, положив её равной, как и раньше, отношению капитала инвестора к стоимости компании. Продолжая аналогичные рассуждения, получим формулы, связывающие доли инвестора, его капитал, инвестиции и стоимость компании для каждого момента времени n = 2 , 3 , ... :

Перейдём к сравнению этих формул с модифицированной формулой (7). Сначала сравним (8) с (7). Вычтем для этого правую часть первой формулы из правой части второй:

nn

E I - " "^-'        E I i

______i=1___i=1 n -n vi"n-1 + E Ii"n-  E Ii + vi i=1            i=1

n

=

n

S =    K n- 1

" ¹    V n- 1 + I n- 1 ’

K n = S n- 1 V n + I n .            (5)

nn

I ' ""-¹^ I i + E I i " "^ v 1 - i =1       i =1

E I i V 1 а¹

n

nn

-    I i     I i α ^n-i

/ (EE I i + V i )( V 1 а¹

n- 1

n

+ Ei- "n-i  = i=1

Подставив (3) и (4) в (5), получим следующее рекуррентное соотношение для K _n :

n

V lE I i " п^{г -}-^г - а "^- 1)

K =-- K n- l--V „ + I„ =

"    V n- 1 + I n- 1 "   "

(EE I i + V 1) V^V i " n^{- 1} + EE I i " n-i)

и оценим числитель полученной дроби:

vi ^P ii (an- — an-1) < о i=1

при a >  1.

Итак, при a >  1 (что заведомо выполняется в случае успешного стартапа) доля инвестора, рассчитанная по формуле (8), оказывается больше доли инвестора, рассчитанной по формуле (7). Заметим, что доля разработчиков равна 1 — S , поэтому для неё будут иметь место обратные соотношения. А именно: при использовании формулы (7) доля разработчиков оказывается больше доли разработчиков, рассчитанной с учётом (8). Следовательно, формула (7) лучше учитывает интересы разработчиков.

Сравним теперь формулы (9) и (7). Важнейшее отличие формулы (7) состоит в том, что она задает долю инвестора S не как число, а как функцию α , имеющую смысл при всех положительных значениях α . При этом, в чем нетрудно убедиться, (9) является частным случаем (7) — при одном выделенном значении a , а именно: a = 1 + r .

Продифференцируем S по α, получим dS = V1 5X1 (1 — i) Iia^i da ~ (Vi + £n=i Iia1 -i)2 ’

(1о)

При n = 1 производная обращается в 0, и это означает, что S постоянна. Действительно, легко убедиться, что в этом случае S равна

ТРУДЫ МФТИ. — 2010. — Том 2, № 1(5) то есть не зависит от α .

При n = 2 , 3 , ... правая часть (10) отрицательна при всех положительных α . Следовательно, при любом из этих n S ( a ) — монотонно убывающая функция. Ранее уже отмечалось, что в успешной компании должно выполняться условие a >  1 + r . Поэтому и в силу убывания S доля инвестора S (1 + r ), рассчитанная по формуле (9), оказывается больше доли инвестора S ( a ), рассчитанной по формуле (7). Поскольку доля разработчиков равна 1 — S , для неё опять будет иметь место обратное соотношение. Следовательно, формула (7) учитывает интересы разработчиков лучше, чем (9).

IV.    Оценка чувствительности модели

Рассмотрим несколько иллюстративных примеров. В каждом из них сравниваются между собой различные варианты развития стартап-компа-нии.

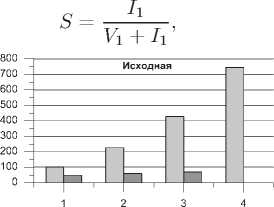
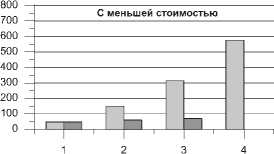
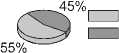
Пример 1. Пусть 1 1 = 50, 1 2 = 60, 1 3 = 70, a = 1 , 5, но в первом варианте V 1 = 100, а во втором — V 1 = 50.

Соответствующие результаты расчётов показаны на рис. 1. Видно, что во втором варианте доля разработчиков уменьшилась.

СТОИМОСТЬ компании инвестиции

СТОИМОСТЬ компании инвестиции

инвестор разработчик

Рис. 1. Диаграммы к примеру 1

I I инвестор

I I разработчик

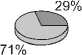
Пример 2. Пусть V 1 = 100, a = 1 , 5, но в первом варианте 1 1 = 50, 1 2 = 60, I з = 70, а во втором — 1 1 = 0, 1 ₂ = 0, 1 3 = 180.

Заметим, что сумма инвестиций в обоих случаях одинакова, но они по-разному распределены во времени. Результаты расчётов проиллюстрированы на рис. 2. Во втором варианте доля разработчика возросла.

Пример 3. Пусть 1 1 = 50, 1 ₂ = 60, 1 3 = 70, V 1 = 100. И пусть теперь a меняется во времени, например, в первом варианте a 1 = 1 , 2, a 2 = 1 , 5, a з = 2, а во втором, наоборот, a 1 =2, a 2 = 1 , 5, a з = 1 , 2.

На рис. 3 видно, что во втором варианте доля разработчика будет больше.

Пример 4. Пусть 1 1 = 100, 1 ₂ = 100, 1 3 = 100, V 1 = 100, в одном случае a = 1 , 2, во втором a = 1 , 5, в третьем a = 5.

Заметим сначала, что значение a = 5 вполне реально. Напомним в этой связи, что мы рассматриваем стартапы. А стартап — такой период в развитии и становлении компании, пройдя который компания увеличивает свою стоимость в десятки и сотни, а то и в тысячи раз.

Например, стоимость компании Google в 1997 году составляла не более $ 500 тыс., а в 2004 го- ду — уже $ 21,7 млрд. За 7 лет стоимость компании увеличилась в 42 тысячи раз. Это значит, что а для компании Google в эти годы составило около 4,5.

Проследим за динамикой доли инвестора в каждом из трёх предложенных вариантов. Инвестор вкладывает в компанию деньги в каждом периоде, поэтому его доля всегда увеличивается. Но на рис. 4 видно, что чем больше коэффициент а , тем меньше эта доля и тем медленнее происходит её рост.

инвестор разработчик

Рис. 2. Диаграммы к примеру 2

инвестор разработчик

।    । инвестор

I    I разработчик

58%---

инвестор разработчик

Рис. 3. Диаграммы к примеру 3

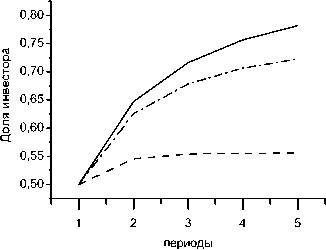
Рис. 4. Зависимость доли инвестора от α

α

α

α

V.    Выводы

На основании рассмотренных примеров можно сформулировать ряд гипотез, относящихся к распределению долей инвестора и разработчиков в стартап-компании. Мы придали этим гипотезам форму рекомендаций, целью которых является увеличение доли разработчика в стартап-ком-пании.

Итак, для увеличения доли разработчика необходимо, чтобы

• —    первоначальная стоимость компании была как можно больше;

• —    инвестиции от внешнего инвестора делались как можно позже (конечно, без ущерба для развития компании);

• —    значения а были как можно больше;

• —    высокие значения а реализовывались в стар-тап-компании как можно раньше.

Насколько эти рекомендации соответствуют действительности, должны показать дальнейшие исследования, в том числе исследования деятельности реальных инновационных компаний.