О среднемаксимальных значениях очeредей в системах массового обслуживания

Методы и результаты анализа телетрафика применяются для оптимального распределения телекоммуникационного ресурса, выделенного для оказания услуг абонентам связи. Эти методы в основном базируются на теории систем массового обслуживания (СМО) и до настоящего времени не утратили своего ведущего положения.

В классической теории СМО основополагающим является предположение о взаимной независимости событий. Переход на новые технологии связи, основанные на принципах пакетной коммутации, существенно изменил свойства телекоммуникационного трафика.

Особенные изменения свойств произошли в трафике мультисервисных сетей доступа. Это привело к существенным ошибкам при его анализе традиционными методами СМО, не учитывающими пачечный характер трафика. Имеется множество публикаций, учитывающих свойства мультисервисного трафика. Результаты исследований, отраженные в этих публикациях, свидетельствуют о том, что подход к анализу трафика с использованием моделей СМО не утратил своего значения и после соответствующей интерпретации характеристик может использоваться для расчета ряда показателей современных сетей

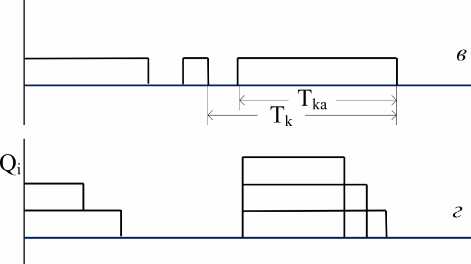
Рисунок 1. Временные диаграммы образования очередей связи. Еще Л. Клейнроком [1] показано, что длина очереди одноканальной СМО в общем случае определяется случайной величиной m – числом поступивших заявок, приходящихся на одну обработанную заявку. Разрабатываемый нами интервальный метод [2] позволяет заменить анализ интервалов времени между соседними заявками и интервалов времени обработки заявок, анализом одной случайной величины – числом заявок, поступающих в течение последовательных интервалов времени обработки каждой из них. Показано, что дисперсия и корреляционные свойства указанной случайной величины при заданной загрузке полностью характеризуют средний размер очереди в СМО.

Процесс обработки состоит из последовательности чередующихся периодов занятости обслуживающего канала (канал обрабатывает заявки) и периодов простоя, в течение которых заявки в обслуживающем канале отсутствуют.

Циклы обслуживания

На рисунке 1 показаны заявки, поступающие в СМО, и заявки, покидающие СМО (расположены ниже оси времени). N_i и M_i соответственно – числа заявок, поступивших и покидающих СМО с начала отсчета. Заявки покидают СМО в моменты времени t 1 , 1 2 , 1 3 , .... На рисунке 1, а показаны графики изменения чисел заявок W i , находящихся в СМО. Здесь же представлены интервалы θ _i между соседними заявками, покидающими СМО. На каждом из интервалов может поступить одна или несколько заявок (например, на интервале θ ₁ поступило 3 заявки). Может не поступить и ни одной заявки (например, на интервалах 6 2 и 6 3 ). На рисунке 1, в c показаны циклы работы T_k и периоды занятости T_ka системы.

Процесс обработки заявок носит циклический характер. После каждого периода занятости следует период простоя системы, в течение которого заявки в системе отсутствуют. В одноканальной СМО в течение каждого периода занятости всегда присутствует одна заявка на обработке. Остальные заявки находятся в очереди Qi, график которой представлен на рисунке 1, г. На каждом из интервалов времени, соответствующем периодам занятости, число заявок в системе всегда превышает на одну заявку число заявок в очереди, поскольку эта заявка находится на обработке. Если система находится в режиме простоя, то заявок в ней нет, и очередь также отсутствует. Будем считать циклом промежуток времени между двумя заявками, покидающими СМО и опустошающими ее. Очередной цикл начинается с начала ин- тервала простоя и заканчивается началом следующего интервала простоя, как это показано на рисунке 1.

Рассмотрим цикл Z_k с длительностью цикла T_k и периодом занятости T_ka . Следует отметить, что очередь на последнем интервале периода занятости (активной части цикла) всегда отсутствует. Однако отсутствие очереди на активном интервале цикла еще не свидетельствует, о том, что этот интервал последний. Для стационарного потока заявок m_t ( т ) с конечным математическим ожиданием m_z ( т ) и дисперсией D m ( т ) нами были получены [3] формулы

_______              1               js + 1 ^- js

Q = lim 17 I I ( N s - j )( m. + j - 1). (1) ^s

N ^ N Z s c [ 1 , N ] j = 0

Здесь N - общее число заявок, N_k = j_{k + 1} -- j_k + 1 - число заявок в цикле, j_k - номер первой заявки цикла Z_k , а j - порядковый номер заявки, считая от начала цикла.

Z

Z k ^ [ 1 , N ]

означает суммирование по всем циклам. Из первой формулы непосредственно следует, что с увеличением числа j , т. е. удалением поступающих заявок от начала цикла, их вклад в среднее значение очереди уменьшается. Внутренняя сумма в (1) представляет общее число заявок S_k , находившихся в очереди в течение цикла Z_S , и соответствует площади фигуры очередей, представленной на рисунке 1, г для интервала времени T_k

N k - 1

S k = Z ( N k - j )( m_k + j - 1).         (2)

j = 0

Предельного размера площадь S_{k lim} в течение цикла Z_k достигает в случае, когда все N_k заявок сосредоточены в начале активной части цикла, на первом интервале обработки, как это показано на рисунке 2:

S k lim = 2 N k ( N k - 1).             (3)

Предельное максимальное значение очереди

2 S Q k lim =        = N k - 1.

Nk

Если заявки распределены равномерно по одной заявке на каждый интервал обработки, то очереди отсутствуют и Sk = 0.

Предельное максимальное значение очереди будет наибольшим из возможных максимальных значений при заданной площади S_k . Принимая указанную модель, мы можем определить макси-

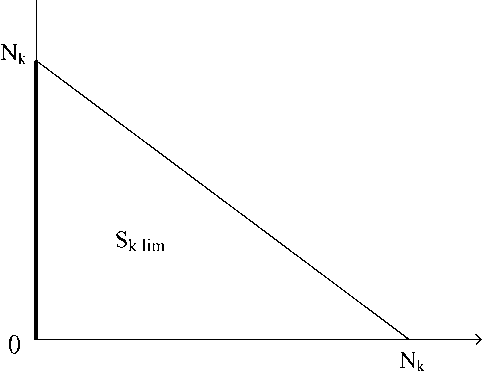
Рисунок 2. Одновременное поступление N _k заявок

мальное значение очереди в течение цикла по измеренному значению S_k .

Q k lim

- 1 + V1 + 8 S k

Очевидно, что

N s = Q k lim

+ 1 =

1 + Л+8 S_k

При достаточно большом значении S_k мы приходим к результату Q _{k lim} = ^2 S_k , приведенному в [4].

Например, показанные на рисунке 1 все заявки цикла находятся на первом интервале Z_k этого цикла. Следовательно, S_{k lim} = 6. Предельного размера очередь в течение цикла также достигает в случае, когда все N_k заявок сосредоточены в начале цикла, на первом интервале обработки:

- k lim

2 S k max N k

= N s - 1 = 3.

Максимально возможное среднее значение очереди

Qk = — = 1,5.

k _{N k}

Если не все заявки сосредоточены в начальном интервале, то максимальное значение очереди уже будет меньше предельного, как это показано на рисунке 3. Так же, как и на рисунке 2, в начальный момент поступает пачка пакетов n 1 _k . Вторая пачка пакетов n _{2 k} поступает со сдвигом на a N_k интервалов. Сумма пакетов обеих пачек равна рассмотренной на рисунке 1 пачке:

^Ns = n 1 s ⁺ n 2 s .

Из рисунка 3 следует, что максимальное значение очереди окажется меньше, чем предельное максимальное значение на величину a N_k . Таким образом, модель, предусматривающая сосредо-

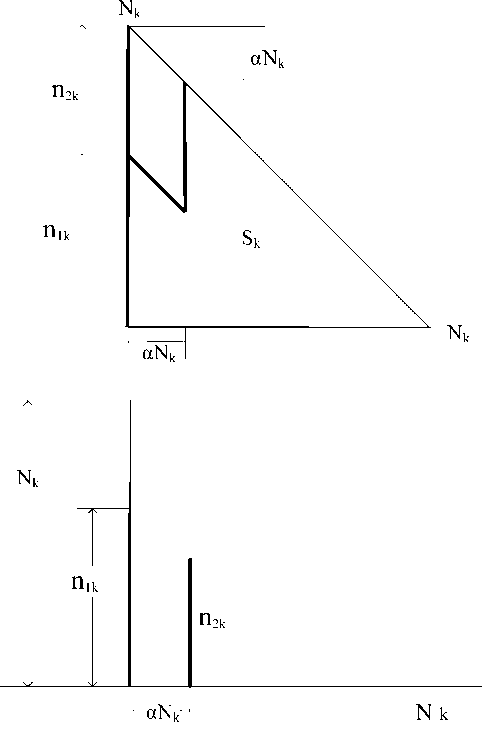
Рисунок 3. Образование очереди двумя пачками пакетов

точение всех пачек заявок (пакетов) в одном, начальном интервале времени приводит к наибольшему из возможных – предельно максимальному значению очереди в данном цикле обслуживания.

Рисунок 3 хорошо иллюстрирует частный случай формулы (1).

Усредняя по циклам, получим среднее значение площади:

K

• s .    = ₇ S ^s. .

K к = 1

Среднее число заявок, поступивших в течение циклов:

K

N . = 7 S N . .

^K к = 1

Среднее из предельно максимальных значений определяется по формуле:

KK

Q kl. m = -S Q .li m = ~ S ( - 1 + Vi + 8 s . ), K к = 1          ² K к = 1

где K – число циклов в рассматриваемой выборке.

При достаточно больших значениях S_k можно пользоваться упрощенной формулой:

KK

Q .li m = - S Q ki m = V S M = ^.

K к = 1          K к - 1

При определении Q.h.m необходимо определение значений Q.um по квадратному корню из среднего значения цикла, что требует значитель- ных вычислительных затрат, поскольку на каждом цикле необходимо вычисление квадратного корня. Мы предлагаем ввести другую оценку среднемаксимальных значений очередей:

QL = Ж .

Такая оценка дает дополнительный запас Q*m > > Qlim, поскольку S^k всегда не меньше ^кЗк • Средние значения очередей определяются по формуле:

q . =

S k

^^^“ • N k

Следует обратить внимание, что Q_k является условным средним значением, когда усреднение очереди производится только в течение периодов занятости и не учитывает периоды простоя [5]. Значения очередей Q . ( р ) и Q l * _m ( р ) существенно зависят от коэффициента загрузки р системы. Поэтому зависимости S . ( р ) необходимо определять при различных значениях этого коэффициента.

Таким образом, вычисление зависимостей средних и среднемаксимальных значений производится по формулам:

Q * ( р ) =^Ж= 1Гтк Q-- ( р ) = N . ( р ) N ( р )

= V 2 s_k ( р ) = 1 2 ^( 2 ) •

^{N к} У K ( р )

Значения Q * _m ( р ) зависят от Q . ( р ):

Q m ( р ) = V 2 Q . ( р ) ^ . ( р )

и возрастают пропорционально квадратному корню из средних значений очередей и чисел заявок в цикле.

Алгоритм

Полученные соотношения позволяют для определения характеристик трафика применить известный алгоритм «Leaky_bucket» [6; 7].

Задаются значение числа N – заявок в эксперименте - и интенсивность обслуживания ц. При каждом появлении заявки на входе в одноканальную СМО на суммирующий вход реверсивного счетчика поступают управляющие сигналы. На вычитающий вход указанного счетчика поступают сигналы от каждой заявки, покидающей СМО. Поскольку каждая заявка поступает в СМО не позже, чем она ее покинет, показания счетчика не могут быть отрицательными. Показания счетчика после момента появления сигналов от заявок, покидающих СМО, характеризуют значения очереди Qi(р') и поступают на накапливающий сумматор. Содержимое сумматора представляет число заявок, находившихся до данного момента в очереди. Ведется непрерывный подсчет чисел заявок, покинувших СМО до тех пор, когда это число достигнет заданного значения N.

Фиксируется время эксперимента T и определяется значение коэффициента загрузки

N

р =---•

µ T

В моменты появления сигналов от заявок, покидающих СМО, проверяется значения показаний счетчика и производится суммирование числа нулевых показаний счетчика (ведется подсчет числа циклов). В момент достижения числа заявок, покинувших СМО, значения N числа циклов достигнет значения K . Таким образом, определяются S ( р ), K ( р ) и N ( р ), по которым находятся значения ^Qk ⁽ р ) и ^Q _lmi ⁽ р ).

Заключение

В предложенной модели трафика за основу берутся суммарные числа заявок в течение циклов их обработки. При постоянной интенсивности обслуживания заявок указанные числа характеризуют площади прямоугольных равнобедренных треугольников. Размеры катетов указанных треугольников характеризуют предельные значения размеров очередей в каждом цикле, а их среднее значение по всем циклам представляет среднемаксимальное значение. Предложенный алгоритм позволяет определить экспериментально как средние, так и среднемаксимальные значения очередей в пачечных потоках трафика мульти-сервисных сетей.