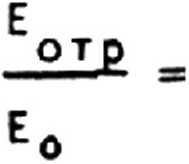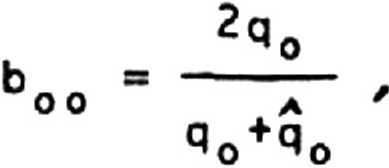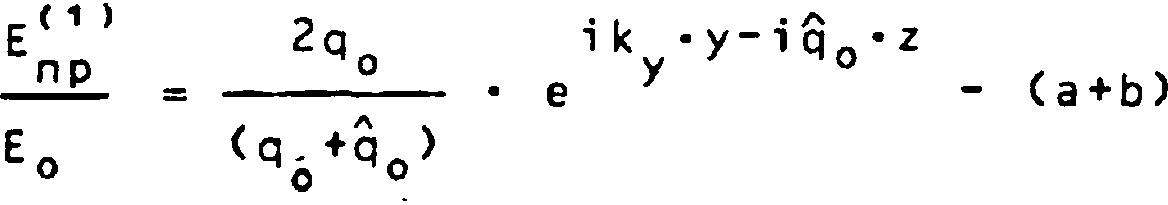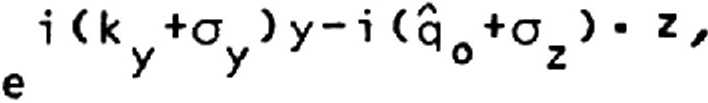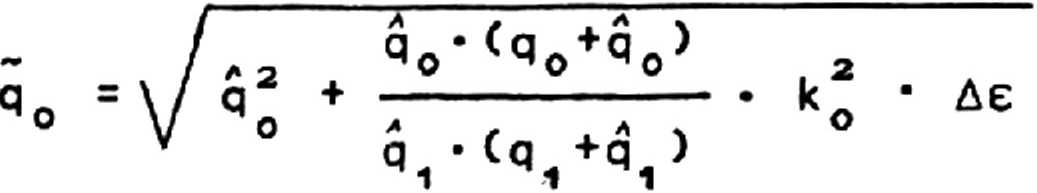О структуре взаимодействия волн с периодически возмущенной средой

О СТРУКТУРЕ ВЗАИМОДЕЙСТВИЯ ВОЛНС ПЕРИОДИЧЕСКИ ВОЗМУЩЕННОЙ СРЕДОЙ

Исследования дифракции плоских волн на голографических решетках, а также проблемы управления параметрами излучения вызывают интерес к структуре полей в периодических средах [1,2].

В данной работе рассматривается падение s-поляризованной волны Е = (E(y_zz)« ■е ^1Ш^_л 0, 0) из полупространства z > 0 с диэлектрической проницаемостью £ = const на среду (z < 0) с неоднородным возмущением Е_ = £ + Ae(y_zz). При этом структура полей определяется уравнениями Гельмгольца Ск₀ = ш/с):

Э2Е . Э2Е (

2 ко

Е • Е = 0 при z > 0

+ к² • е • Е = -к² • Д£<у,г)-Е при z < 0

Эу2 3z2     °                 0

и стыковкой граничных условий:

z = + 0 = E|z = -0

ЗЕ

z = + 0

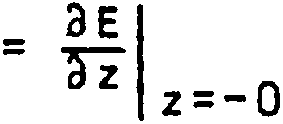
С2)

Теория возмущений, традиционно применяемая для подобных задач, может быть построена различными способами [1*3]. Ниже предлагается рекурентная схема решения системы эквивалентных (1), (2) интег родифференциальных уравнений. Пусть i к -у - 1 к -Z

Е( y.z > 0> = Е + Е где задана падающая волна Е = Е "е            2 ,

2     2     2 ПЭД ОТР                                   ПЗД 0

Ск + к = к '£), а отраженная Е и преломленная Е = E(y.z < 0> описывается у z о                         от р                      пр вытекающими из (1) уравнениями:

Е (y,z > 0) =  / dy'-g. СД ,z)-E    Су’,0);(3)

отр                -оо        к у' отр '*

ОО

Е (уZz < 0) =  / dy'-Q'C/zj-E (y*zO)+F;(4)

пр            -«о      ку' пр

F = /dz 1 • / d у • G с (Д ,г1,г)'к2-ДЕ<у,/г,)-Е ( у * z z * ) ,(5)

о                  к у                             пр где G и g определяются с учетом условий излучения функциями Ханкеля Н(1} [3]:

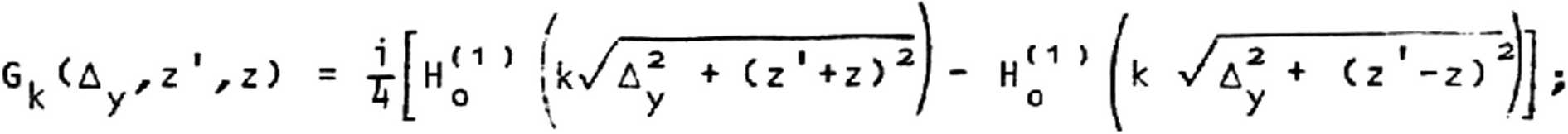
д, (Д z z)

як у'

3G. (Д z z 1 z z )

___к У

Э Z *

z * =0

к = к V^E . к = к _ V Е, Д = у

О                   О * у z

При этом граничные условия (2)

i к • | z |

2/Д2 + z2 У

" У • сводятся К

Н (1 у ( к х/д2 + z 2 ) ; 1             У

соотношению:

Уравнения (4)-(6) позволяют построить разложенце Enp(yzz) по степеням Де, 1 к -у после чего определяется EQTp(yzO) = ^np^z^^ ” ^о'е ^ и 8 соответствии с (3) находится EQTp

Будем рассматривать отклик на периодическое возмущение io -у - io,-z

А                        V 'Z

Д e(yzz) = Де-е ’

Тогда, вводя q = \/к^ - (к +т-о I1, q = Vк2 - (к +то )2Z (q = к z q= £ )z(7)

у у т               у у *z '

на основании изложенной схемы получим интересующую нас структуру полей:

b mn

-i

( q^-qik-y + iq^z

где для коэффициентов b реализуются рекурентные соотношения:

k2-b -    .

₌о m -1 _z п -1

тП (Vn+n'°2)2’^ m-n z m

m

mo , mn n = 1

(q +q +n-o ) m m-n z

(q +q )

Полученное решение (8)-(10) удовлетворяет исходной системе (1)-(2), что мо

жет быть проверено непосредственной подстановкой. Соотношения (8), (9) наглядно

демонстрируют возникновение серии боковых лучей в каждом порядке теории возму

щений по Де. При этом для каждого порядка m реализуется один отраженный луч с конечной амплитудой ~(Де)т и (т + 1) преломленных. Как и следовало ожидать [2], направления отраженных лучей характеризуется углами <р к оси z: m sin ф = (k +ma )/k = sin a * m • — z m у у                              z где

• a - угол падения (sin a ⁼ k /k);

• A = 2n/k - длина волны;

• г = 2n/a ~ продольный масштаб неоднородности возмущения Д^Ае.

Несколько сложнее описание преломленных лучей, амплитуды которых имеют, согласно (10), резонансный характер при о= (^_m - ^_т__п)/п, Соответствующий предельный переход целесообразно обсудить, ограничиваясь первым порядком теории возмущений. В этом случае из (8)-(10) имеем компактные выражения:

Е( ,q -q \ ik *y+iq -z i(k +o )-y+iq^*z отр / о o\ у ' Mo -         У У        1

----— = ( --------j • e '                   а • e '

Eo    %+%

i ( к +o ) • у-i q •z _e    у у

где

₌        ^2ко * ^Де * %

(q +q ) (q +q ) (q + q +o ) О О 11 О 1 z b _      2ko * Де * %

‘ [(no+az>2-q^]

Из (11)-(14) ясно, что в резонансном случае c?z * сТ = ^"Яо амплитуда а

(13) отраженной волны остается конечной. В преломленной волне при этом происхо

дит слияние находящихся в противофазе боковых лучей. Соответствующая структура

поля, обеспечивающая различные предельные переходы, имеет вид:

Е(рез)     2q       i(k +о )-y-iq -z np =      °   . e У У 1     +

Eo     %♦%

2Я0 iky*y-i%-2 i(ky+ay)-y-iq,-z где

qi = Vqi+k0 • ДЕ •

Действительно, при |kQ-AE*z| « 1 и I

—— = —     • e            ,

Eo Vkz где k = v k •(е+де) - k Z       О      °        у

В заключение следует отметить, что при малых о рассмотренная резонансная ситуация реализуется, если с ортогонален к направлению не возмущенного луча:

о -к + о^рез-к = о У У z ^KZ