О структурировании лабораторно-практических занятий при изучении дисциплин программирования

При подготовке специалистов и бакалавров инженерных направлений и профилей многие дисциплины федерального компонента учебного плана базируются на математических знаниях технического вуза и программирования. Такие дисциплины, как правило, сопровождаются лабораторными и/или практическими занятиями. В частности, в направлении «Информатика и вычислительная техника» по профилю «Автоматизированные системы обработки информации и управления» есть дисциплины «Программирование», «Технологии программирования», «Программная инженерия». По рекомендации Минвуза РФ включается в учебный план также дисциплина «Основы автоматики» и пр. Названные дисциплины базируются на многих математических разделах технического вуза. В связи с этим лостаточно актуальным является сбалансированное включение в лабораторный практикум математических знаний, программирования и собственно изучаемой дисциплины. Даже в программировании ряд математических аспектов требует тщательного изучения для программного решения учебных задач. Поэтому авторы считают, что в структуре лабораторного практикума каждой лабораторной работе должно быть уделено особое внимание в плане улучшения математических компетенций обучающихся. Этому должно способствовать тщательный подбор примеров (задач), с теоретической базой, необходимой для их решения и программирования. Авторы опираются на свой многолетний опыт в проведении учебно-практических занятий в Национальном исследовательском университете им. Н.П. Огарёва по направлению «Информатика и вычислительная техника» в соответствии с профилем «Автоматизированные системы обработки информации и управления».

Методика структурирования

В век Интернета можно найти практически любую информацию, в том числе и при изучении какой-либо учебной дисциплины. Особенно это необходимо при дистанционном и заочном обучении. Однако при очной форме обучения на аудиторных

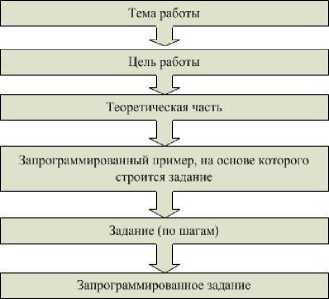
Рис.1 Структура описания лабораторно-практического занятия

занятиях можно рекомендовать акцентировать работу совместно с преподавателем, предполагая, что он является носителем знаний. Личный контакт способствует лучшему пониманию и усвоению предмета или какого-то учебного раздела. При этом обучаемому не надо тратить время на поиск в Интернете возможно тривиальных вопросов, и не только тривиальных. В тоже время учебно-практический материал должен быть тщательно подготовлен. Во-первых, должна быть проработана тема для практического изучения. Во-вторых, в теме следует отра- быть достаточен для выполнения

зить два раздела или части по изучению материала: теоретическую и практическая части. В-третьих, материал занятия должен учебно-практической работы. Предполагаемая структура материала для лабораторно-практического занятия представлена на рис.1. Обучаемый не должен тратить время на поиски каких-то вопросов и ответов при выполнении предложенных заданий в виде задач и примеров. Конечно, предполагается, что обучаемый (студент) посещает часы лекционного курса. В связи с этим, теорети- ческая часть описания учебно-практического занятия не должна изобиловать математическими выкладками, доказательствами и пр. для получения результатов, необходимых для выполнения работы. Обычно необходимы только конечные результаты с их практической интерпретацией. Практическая часть сопровождается примерами и задачами, которые способствуют освоению теоретического материала как данного лабораторно-практическкого занятия, так и лекционного курса по данной теме. Авторы считают, что все практические примеры должны быть представлены с решениями и программной реализацией. В связи с этим, у преподавателя возникает необходимость в структурированности лабораторно-практических занятий, которые бы способствовали развитию математического мышления и способностей при изучении той или иной учебной дисциплины. Приводимые примеры должны порождать задания к приведенному решению, к изучению необходимых вопросов для получения решения самомтоятельно. Конечно, преподаватель обязан объяснить поиск решения задания. В некоторых случаях, может быть применена демонстрация конечного результата, например, результата программирования. Как показывает опыт, это бывает достаточно, чтобы активизировать деятельность в решении и программировании соответствующей задачи. В противном случае следует дать постепенное объяснение решения задачи в том ключе, чтобы возникало собственное понимание или понимание того, что некоторые разделы курса необходимо дополнительно изучить или повторить. В большей мере подобная структура учебно-практических занятий отражена в [1–3].

Примеры практических заданий

Рассмотрим некоторые характерные примеры, которые по нашему мнению удачно совмещают развитие навыков программирования и закрепление математических компетенций.

Пример 1. Заполнить массив случайными числами, распределенными, например, по равномерному закону, и определить среднее арифметическое значение и дисперсию. Размер массива определяется динамически во время выполнения программы. Решение выполнить на языке С/С++ в MS Visual Studio (2012, 2013).

Первоначальный анализ условия примера указывает на то, что в программе следует использовать указатели и предусмотреть динамическое выделение памяти. Во-вторых, расчет среднего арифметического значения не вызывает затруднений. А вот с дисперсией нередко бывают неокоторые неточности. Обычно вычисляется средневыборочная дисперсия D по формуле

1 n

D = -£ (Xi — x )2, ni=1

где n – размер выборки, x _i – случайная величина, x – среднее арифметическое значение исследуемой выборки чисел, вычисляемая по формуле

_   1 n

X = —^ Xi.

n i = 1

Здесь надо отметить, что приведенная формула расчета дисперсии есть состоятельная, но смещенная оценка дисперсии генеральной совокупности [4]. Вообще, надо применять несмещенную оценку дисперсии, а именно

1 n .

D = —;Ё ^{( x} i - ^x ) • n - 1 i = 1

В плане программирования особых проблем нет. Приведем возможный программный код решения примера на языке С:

/*

* Пример расчета исправленной выборочной дисперсии

*/

#include

#include

#include const int N = 123456789; // размер одномерного массива int main(void) { double a = 1.0,    // левая граница интервала b = 5.0; // правая граница интервала double Mx = 0.0,  // среднее

D = 0.0;  // исправленная выборочная дисперсия double *ptr;      // указатель на тип double int i;

// Выделение памяти под массив вещественных чисел ptr = (double*) calloc(N, sizeof(double));

if (ptr == NULL) { printf("\n Memory is not allocated. Press any key: ");

_getch();

exit(1); // завершение выполнения программы }

// Заполнение выделенной памяти равномерно

// распределенными случайными числами из интервала [1, 5]

for (i = 0; i < N; ++i) { ptr[i] = a + (b - a)*rand()/RAND_MAX;

// RAND_MAX = 32767, не менее }

// Расчет среднего арифметического выборки - массива for (i = 0; i < N; ++i) {

Mx += ptr[i];

}

Mx /= N;

// Расчет исправленной выборочной дисперсии for (i = 0; i < N; ++i) {

D += (ptr[i] - Mx)*(ptr[i] - Mx);

} // фигурные скобки не обязательны

D /= (N - 1);

free(ptr); // освобождение памяти

// Результаты printf("\n Mean = %g; Variation = %g\n", Mx, D);

printf("\n Press any key: ");

_getch();

return 0;

}

Возможный результат выполнения программы:

Mean = 3.00022; Variation = 1.33356

В этом примере необходимо учитывать, что статические массивы под заданный большой размер не пригодны. Поэтому приходиться выделять память в куче с помощью указателя. Функция rand() – функция генерирования псевдослучайных целых чисел. В данном случае при многократном запуске программы будут получаться одни и те же результаты. Выделение памяти и заполнение ее данными под такой большой размер достаточно трудоемкая операция. В связи с чем возможны улучшения программного кода, для чего необходимы некоторые дополнительные знания из математической статистики.

Теперь можно перейти к формулировке заданий к данной программе:

• 1.    Дополните программный код инструкцией, позволяющей получать различные результаты при многократном выполнении программы.

• 2.    В программе примените только один цикл расчета среднего значения и исправленной выборочной дисперсии.

Первое задание состоит на знание функций стандартной библиотеки языка С, следует применить функцию srand(). Второе задание оптимизирует программу, сокращает количество длительных циклов (N = 123456789 – велико). Для его выполнения необходимы знания по математической статистике. Как известно [4], дисперсия – это математическое ожидание от квадрата отклонения случайной величины x от своего математического ожидания M x , т. е.

D = M [(x - Mx )2].

Вместо математического ожидания M x вынуждены использовать среднее арифметическое значение m _x – несмещенную оценку математического ожидания. В результате, как указывалось выше, будет применяться выборочная дисперсия, которая является смещенной оценкой истинной дисперсии – дисперсии генеральной совокупности. Для решения задания к программе раскроем выражение определения дисперсии:

D = M[(x-Mx)2] = M[x2 -2xMx + Mx"] = M[x2]-2MxM[x] + Mx =

= M [ x 2] - 2 Mx + Mx? = M [ x 2] - Mx?.

Таким образом, дисперсия D может быть вычислена через известное математическое ожидание и второй начальный момент. Это позволит избежать второго цикла в программе при расчете дисперсии. Только опять вместо математического ожидания и второго начального момента (теоретических значений) придется использовать их оценки – средние арифметические значения. В частности, оценка второго начального момента может быть вычислена по формуле

n

M [ x 2] = M 2 = -£ x2.

n i = 1

Для получения несмещенной оценки результат расчета дисперсии следует умножить на n /( n –1) [4].

Пример 2 . Моделирование дискретной системы, состоящей из полидисперсных сфер, заданных своими диаметрами. Моделирование выполнить в MATLAB с построением плоской модели.

Полидисперсность реализуется по определенной закономерности, заключающейся в том, что в свободном пространстве трех плотно сомкнутых сфер теку- щего подмножества размещается касающаяся их сфера последующего подмножества [6].

Плоская модель элемента дискретной системы, состоящей из полидисперс-ных сфер, приведена на рис. 2.

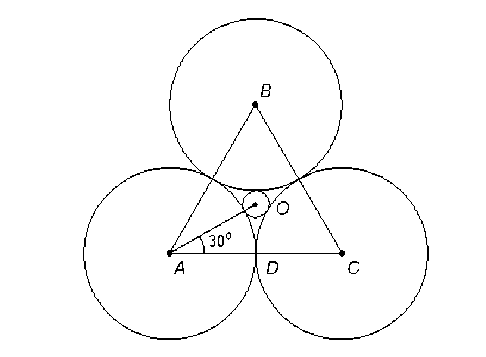
Рис. 2. Модель элемента дискретной системы, состоящей из полидисперсных сфе р

Обозначим через r и R радиусы малой и больших окружностей. Задача заключается в определении связи между радиусами большой и малой окружности. Треугольник ABC является равносторонним, поэтому угол ∠ OAC равен 30^o ( π /6). Рассмотрим прямоугольный треугольник AOD . Очевидно, что сторона (гипотенуза) AO равна сумме двух радиусов, т. е. AO = R + r . В свою очередь катет AD есть большой радиус R, следовательно, AD = R . Выразим AO в следующем виде: R + r = R /cos( π /6). Разделив обе части уравнения на R , получим

• 1    + r / R = 1/cos( π /6); r / R = 1/cos( π /6) – 1 = 1.1547 – 1 = 0.1547.

Полученный результат означает, что r = 0.1547 ⋅ R . При подобном рассмотрении можно получить аналогичную зависимость между следующими подмножествами. Обобщая, для n -го подмножества будем иметь r n = (0.1547) ⁿ ⋅ R [6].

При моделировании можно напрямую использовать константу в виде выражения 1/cos( π /6) – 1.

В соответствии с полученным результатом программа моделирования в MATLAB может быть представлена в виде следующих трех функций:

function task3

%% Модель полидисперсных сфер

%% x0, y0, R - координаты центра и радиус базовой окружности

%% Nt - число точек базовой и последующих окружностей

%% n - число уровней самоподобия

%% Три сферы имеют точки соприкосновения, не пересекаются clc,close all x0 = -7 + 14*rand; % из [-7, 7] по равномерному закону y0 = -5 + 10*rand; % из [-5, 5] по равномерному закону

R = randi([3, 21]); % случайный размер радиуса, целое число

Nt = 2000;

n = randi([1,4]); %% 4, 5, 6, ...

о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/о/ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

[ R3, Rn, XYC, XT, YT ] = Repeat(R, x0, y0, Nt);     %% пользовательская функция

Dgram(Nt, x0, y0, XYC, XT, YT, 1, R, R3, Rn, false, n);

for k = 1 : n

[ R3, Rn, XYC, XT, YT ] = Repeat(Rn, x0, y0, Nt);

Dgram(Nt, x0, y0, XYC, XT, YT, 1, R, R3, Rn, false, n);

end end %% end function task3

function [ R3, Rn, XYC, XT, YT ] = Repeat( R, x0, y0, Nt )

% Функция создания массивов для построения окружностей

% Прототип функции:

% [ R3, Rn, XYC, XT, YT ] = Repeat( R, x0, y0, Nt )

% Аргументы функции:

% R - радиус порождающей окружности

% x0, y0 - координаты центра порождающей окружности

% Nt - число точек окружностей

% Возвращаемые значения:

% R3 - радиусы трех окружностей

% Rn - радиус малой вложенной окружности

% XYC - массив координат центров трех окружностей

% XT, YT - массивы для построения трех окружностей x1 = R*cos(pi/6);

R3 = x1*R/(x1 + R);% радиусы трех окружностей

D = 2*R3; % диаметр каждой из трех окружностей d = D*(1 - cos(pi/6))/cos(pi/6); % диаметр малой окружности

%%% z = d/D; % z = 0.1547 - const

%% Радиус малой внутренней окружности

%% между тремя большими окружностями

Rn = d/2;

%% Возвращаемые массивы построения вложенной окружности t = linspace(0, 2*pi, Nt);

%% Массив для координат центров трех окружностей

XYC = zeros(3,2);

%% Цикл построения трех окружностей

XT = zeros(3, Nt); % координаты X для трех окружностей

YT = zeros(3, Nt); % координаты Y для трех окружностей k = 0;

for ug = -pi/6 : (pi/2 + pi/6) : 2*pi k = k + 1;

%% Координаты центров малых окружностей xm = (R-R3)*cos(ug) + x0;

ym = (R-R3)*sin(ug) + y0;

xt = R3*cos(t) + xm;

yt = R3*sin(t) + ym;

if k < 4

XYC(k, 1 : 2) = [xm, ym]; %% сохранение в массиве

XT(k, 1 : Nt) = xt;

• YT(k, 1 : Nt) = yt;

end end %% end for end %%% end Repeat()

function Dgram(Nt,x0,y0,XYC,XT,YT,gnum,R,R3,Rn,da,n)

% Прототип функции:

% Dgram( Nt, x0, y0, XYC, XT, YT, gnum, R, R3, Rn, da );

% Аргументы функции:

• %    Nt - число точек окружностей

• %    x0, y0 - координаты центра порождающей окружности

• %    XYC - координаты центра трех окружностей

• %    XT, YT - массивы для построения трех окружностей

• %    gnum - номер диаграммы

• %    R - радиус порождающей окружности

• %    R3 - радиус каждой из трех окружностей

• %    Rn - радиус вписанной окружности

• % da - булевый тип, для построения меток центров окружностей

% n - число уровней самоподобия figure(ceil(gnum))

%% Порождающая окружность t = linspace(0, 2*pi, Nt);

x = R*cos(t) + x0;

y = R*sin(t) + y0;

line(x,y,'color','k', 'lines', ':') % порождающая окружность hold on

%% Координаты центральных окружностей if da line(x0, y0, 'marker', 'o', 'markersize', 4, 'color', 'k', 'markerfacecolor', 'k') end grid off

%% Одна вложенная окружность xr = Rn*cos(t) + x0;

yr = Rn*sin(t) + y0;

line(xr, yr, 'color', 'k')

%% Построение центров трех окружностей for k = 1 : 3

if da line(XYC(k,1), XYC(k,2), 'marker', 'o', 'markersize', 4, 'color', 'k', 'markerfacecolor', 'k')

end line(XT(k, :), YT(k, :), 'color', 'k')

%% три окружности, сдвинутые на 120 градусов угловых end

%% Границы координатных осей xlim([min(x)- R/10, max(x) + R/10])

ylim([min(y)- R/10, max(y) + R/10])

z = Rn/R3;

title([ ' r_0 = ', num2str(R3), '; r_1 = ', num2str(Rn), '; r_1/r_0 = z = ', num2str(z), '; n = ', num2str(n)],...

'FontName', 'Consolas','fontsize', 10, 'FontWeight', 'demi')

xlabel('\it\fontsize{14}\fontname{georgia}x')

ylabel('\it\fontsize{14}\fontname{georgia}y') axis equal set(gcf, 'name', 'Плоская модель полидисперсных сфер', 'color', 'w') end % end Dgram()

Пример выполнения программы показан на рис. 3.

Гу = 0.0025764; г, = 0.00039858; Г^Гу = Z 0.1547; П = 3

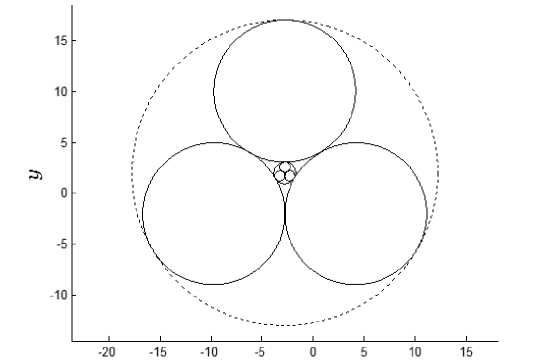
Рис. 3. Модель полидисперсных сфер с уровнем самоподобия n = 3

По данной программе может быть предложено следующее задание: распространить построение подмножеств подобных фигур в каждой из окружностей, выполнить в пространстве. Возможно, следует привести образцы заданных диаграмм без представления реализующего программного кода.

Заключение

Рассмотрены этапы структурирования учебно-практического практикума инженерных специальностей для дисциплин, связанных с программированием. Приведенные примеры в различных средах программирования раскрывают предложенную структуру создания описания лабораторных работ, показывают соотношения между теоретическим и практическим наполнением практикума. Отмечается необходимость развития математических компетенций при написании программ по решению поставленных задач. В качестве образцов выполнения лабораторного практикума можно рекомендовать работы авторов [1–3].

Развитию математических компетенций посвящен реализуемый при поддержке Европейской Комиссии проект «Современные образовательные технологии преподавания математики в инженерном образовании России» в рамках гранта программы Темпус 543851-TEMPUS-1-2013-1-DE-TEMPUS-JPCR). Основой проекта является электронная система поддержки обучения математики Math-Bridge , позволяющая реализовывать различные педагогические стратегии и обучающие сценарии. Платформа разработана консорциумом европейских вузов и является распределенным инструментом поддержки технологии расширенного обучения ( Technology-Enhanced Learning). Анализ возможностей Math-Bridge показал, что предлагаемый подход к структурированию лабораторно-практических занятий органично реализуется в предлагаемых системой сценариях обучения.

Данный проект профинансирован при поддержке Европейской Комиссии в рамках программы Темпус (№ гранта: 543851-TEMPUS-1-2013-1-DE-TEMPUS-JPCR). Эта публикация отражает исключительно взгляды авторов. Комиссия не несет ответственности за любое ис- пользование информации, содержащейся здесь

This project has been funded with support from the European Commission.

This publication [communication] reflects the views only of the author, and the Commission cannot be held responsible for any use which may be made of the information contained therein.