О связи константы распространения блоховской поверхностной волны с толщиной верхнего слоя фотонного кристалла

Изучение свойств поверхностных электромагнитных волн (ПЭВ), распространяющихся в различных диэлектрических и металлодиэлектрических структурах, привлекает в последнее время большое внимание, связанное как с фундаментальным интересом, так и с перспективами их применения в различных областях [1]. Наибольшее число работ посвящено поверхностным плазмон-поляритонам (ППП), распространяющимся вдоль границ раздела металла и диэлектрика, и плазмонным модам, распространяющимся в более сложных металлодиэлектрических структурах различной конфигурации. Несмотря на локализацию энергии плазмонной моды в субволновой области, достижимую в некоторых плазмонных волноводах, существенным недостатком таких структур являются высокие потери на поглощение в металле, прямо пропорциональные степени локализации энергии моды. При этом существует тип ПЭВ, которые могут распространяться в полностью диэлектрических структурах. Такие волны называются блохов-скими поверхностными волнами (БПВ) [2–6] и распространяются вдоль границ раздела между однородной средой и фотонным кристаллом или между двумя различными фотонными кристаллами. В случае, когда все материалы структуры – диэлектрики, потери на поглощение при распространении такой поверхностной волны могут быть практически полностью устранены. Отсутствие потерь на поглощение делает БПВ перспективными в различных приложениях, в частности, в химических и биологических датчиках [7–12], а также в интегрированных на кристалле элементах интегральной оптики [13 – 18], предназначенных для передачи и обработки информации.

Несмотря на то, что дисперсионные соотношения для БПВ, распространяющихся вдоль границы раздела одномерного диэлектрического фотонного кристалла (ФК) и однородной среды, были исследованы в различных работах [2–6], в известных работах не приведено явного аналитического выражения, опре- деляющего связь константы распространения (эффективного показателя преломления) БПВ с толщиной верхнего слоя ФК. Данное соотношение представляет большой интерес при расчёте элементов «двумерной оптики» для управления распространением БПВ (линз, призм, делителей пучка, брэгговских отражателей, спектральных и пространственных фильтров и т.д.). Как правило, расчёт таких элементов основан на методе эффективного показателя преломления [19]. Изменение толщины верхнего слоя ФК изменяет эффективный показатель преломления (нормированную на волновое число константу распространения) БПВ и, таким образом, позволяет «кодировать» профиль эффективного показателя преломления аналогично «обычному» оптическому элементу, предназначенному для заданного преобразования плоской волны, распространяющейся в свободном пространстве [16 –18]. В настоящей работе рассмотрен вывод дисперсионного уравнения БПВ в случае, когда толщина верхнего слоя ФК является произвольной. На основе полученного дисперсионного уравнения записано явное аналитическое соотношение, определяющее связь константы распространения БПВ с толщиной верхнего слоя ФК.

• 1.    Дисперсионное уравнение БПВ

Приведём вывод дисперсионного соотношения БПВ, распространяющейся вдоль границы раздела полубесконечного одномерного ФК и однородной среды. Поле такой ПЭВ является затухающим при удалении от границы раздела. В однородной среде, находящейся над ФК, поле соответствует затухающей плоской волне. В области фотонного кристалла поле соответствует затухающей «объёмной» моде одномерного ФК.

Для получения дисперсионного соотношения ПЭВ необходимо записать общее представление поля в области ФК и в однородной среде над ФК. Рассмотрим случай TE-поляризации, при котором E = (0, Ey, 0), H = (Hx, 0, Hz). Пусть период ФК состоит из двух однородных слоёв с толщинами h1 и h2 (d = h1 + h2) и ди- электрическими проницаемостями е1 и е2, е1> е2. Электрическое поле в слоях кристалла при –d ≤ z <0 может быть представлено в виде суперпозиции двух плоских волн противоположных направлений:

E y ,1 ( x ^, z ) = exp ( ik x , 0 x ) { Ct exp ( ik z , 1 z ) ⁺

ставляя получаемые выражения в шестое уравнение, получим:

² k z ,1 k z ,2 sin ( k z ,1 h 1 ) cos ( k z ,2 h 2 ) ⁺

⁺ ( ^kz ²,1 ^{+ k}z ²,2 ) cos ( ^kz ,1 h 1 ) sin ( ^kz ,2 h 2 ) ^-

+ C 1 exp ( - ik 1 z ) } , - h 1 <  z <  0,

E y ,2 ( x , z ) = exp ( ik x , 0 x ) { ^C 2 exp ( ^ikz , 2 [ z ⁺ h l ] ) ⁺

+ C - exp ( - ik_{z 2} [ z + h 1 ] ) } , - d <  z < - h 1 ,

где C ( i =1,2) - неизвестные коэффициенты, k_z i = V k 02 e i - k 20 , k 0 = 2 п / X — волновое число, X - длина волны. Будем теперь считать, что верхний слой ФК «продолжен» или «обрезан» до прямой z = h ₀, h ₀ > – h ₁, соответствующей границе распространения ПЭВ (рис. 1).

Поле над границей раздела z = h 0 соответствует затухающей плоской волне:

E y ,0 ( x , z ) = exp ( ^ikx , 0 x ) exp ( ^ikz , 0 [ z ^{- h}0 ] ) , z >  ^h 0 ^{, (2)} где k_z , ₀ = ^ k ₀ ² е ₀ - k ² ₀ . Для существования электромагнитного поля, имеющего вид плоской волны (2) при z >  h 0 и вид «объёмной» моды ФК при z <  h 0 , необходимо выполнение условий непрерывности тангенциальных компонент поля E y , ₀, H_x ,о да д E y , ₀/ д z и E y ,1 , H_x ,1 да д E y ,1 / д z на границе z = h ₀, условий непрерывности тангенциальных компонент поля E y , i , H_x , i да д E y , i / д z ( i = 1,2) при z =– h 1 и условий квазипериодичности E y ,2 ( x ,- d ) = E y ,1 ( x ,0) ^ ,      H x ,2 ( x ,- d ) = H x ,i ( x ,0) ^ ,      где

£ = exp ( - ikd ), k - волновое число «объёмной» моды ФК. Применяя вышеприведённые граничные условия, получим следующую систему из шести уравнений относительно шести неизвестных: коэффициентов (амплитуд волн) C 1 ⁺ , C 1 ^- , C 2 , C 2 , величины £ и констан -ты распространения БПВ k x ,0 (входящей в систему неявно через величины k z ,0 , k z ,1 , k z ,2 ):

^C exp ( ^ikz , 1 h 0 ) ^{+ C} 1 ^- exp (^{- ik}z , 1 h 0 ) = ¹

^C 1 ^{+ k}z , 1 exp ( ^ikz , 1 ^h 0 ) ^{- C} 1 ^{- k}z , 1 exp (^{- ik}z , 1 ^h 0 ) = ^kz , 0 ,

C 1 ⁺ exp ( - ik z 1 h 1 ) + C 1 ^- exp ( ik z 1 h 1 ) - C 2 - C 2 = 0,

^C 1 ^{+ k}z , 1 exp (^{- ik}z , 1 h )^{- C} 1 ^{- k}z , 1 exp ( ^ikz , 1 h )^-

• •    - C 2" k z , 2 + C 2 - k z , 2 = 0,                                (3)

№ ^C 4

• -    C 2 exp ( - ik z ₂ h 2 ) - C ₂ exp ( ik z ₂ h 2 ) = 0,

C 2 k z ,£- C 2 k z 3

• ^-    C 2 k z , 2 exp (^- ik z , 2 h ) ^{+ C} 2 ^k , 2 exp ( ik z , 2 h 2 ) = ⁰.

Последовательно выражая неизвестные C 1 ⁺ , C , C + , C -- , ^ из первых пяти уравнений в (3) и под-

k

-

2 z ,1

-

k ² z ,2

k

2 z ,1

-

² z ,0

sin ( k_{z 2} h 2 ) x

^x { ( ^kz ²,1 ^{+ k}z ²,0 ) ^cos ( ^kz ,1 [ 2 h 0 ⁺ h 1 ] )^-

^{- 2 ik}z ,1 ^kz ,0 sin ( ^kz ,1 [ ^{2 h} 0 ⁺ h 1 ] ) } = 0.

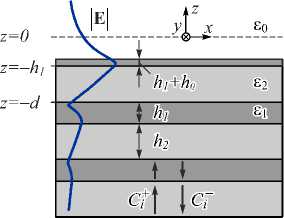
Рис. 1. Геометрия структуры

Уравнение (4) является дисперсионным уравнением БПВ. При заданных длине волны X и параметрах ФК из него может быть найдена константа распространения k x ,0 БПВ.

Система уравнений (3) соответствует граничным условиям для случая ТЕ-поляризации. Для ТМ-поля-ризации граничные условия также можно описать системой уравнений вида (3), однако в этом случае нужно выполнить две следующие замены. Во-первых, величины k z , i , i = 0,1,2 в (3) нужно заменить на k_z , i / е i . Во-вторых, величины h_i , i =0, 1,2 нужно заменить на е i h i . Поскольку при данных заменах вид системы (3) не изменяется, то дисперсионное уравнение (4) будет описывать случай ТМ-поляризации, если в уравнении (4) выполнить вышеуказанные замены:

^kz , i ^ ^kz j/e- , i = ⁰,^1,2, h 0 —> e 1 h 0 , h i —>e i h i , i = 1,2.

2. Анализ связи константы распространения БПВ с толщиной верхнего слоя фотонного кристалла

Из уравнения (4) можно в явном виде определить связь константы распространения k x ,0 с величиной h 0 , определяющей толщину верхнего слоя ФК. Действительно, представим последнее выражение в скобках в левой части (4) как косинус суммы:

^{2 k}z ,1 ^kz ,2 sin ( ^kz ,1 h 1 ) cos ( ^kz ,2 h 2 ) ⁺

⁺ ( ^kz ²,1 ^{+ k}z ²,2 ) cos ( ^kz ,1 h 1 ) sin ( ^kz ,2 h 2 ) =                    ⁽⁶⁾

= ( kz2,1 - kz2,2 ) sin ( kz,2h2 ) • cos ( kz,1 [2h0 + h1 ] + ф) , где kz,i = Vk02ei- k20 , i = 0,1,2, ф = - arccos [(kz 1 + kz2 0) / (kz2 1 - kz 0)]. Отметим, что поле БПВ в однородной среде над ФК соответствует за-

тухающей плоской волне, т. е. величина k_{z ,0} является чисто мнимой. При этом k Z1 + k z 0 <  k 21 - k^ 0 и

|cos ф | < 1.

Из (6) несложно получить искомое выражение для h ₀ в виде

h = ±—-— arccos ⁰       2 k z ,1

2 k k

, 2 z1 / 2 sin ( kz ,1 hl ) ctg ( kz 2 h ) + kz ,1   kz ,2

+

cos ( k_{z ,1} h ₁ )

+--arccos

2 k z ,1

^kz .1 ^{+ k}z .0

k ², V ^z .1

^^^^^™

k ² ₀

z ,0 У

^^^^^™

h  n m

— +--, m e Z.

2     k z ,1

Для ТМ-поляризации в уравнении (7) нужно выполнить замены (5). Согласно (7), величина h ₀ определена с точностью до п / k_z ,1 . Это условие определяет существование БПВ с одинаковыми константами распространения k_{x ,0} при различных значениях h ₀. Аналогично модам плоскопараллельного волновода будем называть такие БПВ модами различных порядков. Кроме того, при некоторых значениях h 0 может существовать несколько БПВ с различными эффективными показателями преломления [17].

Напомним, что дисперсионное уравнение (4) определяет поле, имеющее вид плоской волны (2) при z >  h 0 и вид моды ФК при z <  h 0 . В ФК всегда существуют две моды противоположных направлений с константами распространения ± k . Знаки «±» у первого слагаемого в правой части уравнения (7) как раз описывают случай этих двух мод. В фотонной запрещённой зоне одна из мод является затухающей в направлении от границы раздела (| ^ |< 1), а вторая - возрастающей (| ^ |> 1). Следовательно, решения уравнений (4) и (7) будут соответствовать ПЭВ только при выполнении следующих условий: k x , ₀> k ₀ е ₀ (условие затухания плоской волны (2) в области над ФК) и | ^ | < 1 (условие затухания моды ФК в направлении от границы). Таким образом, при расчёте h 0 по заданному k x ,0 необходимо в уравнении (7) выбирать знак первого слагаемого в соответствии с условием | ^ |< 1. Выражение для £ может быть получено последовательным выражением коэффициентов C 1 ⁺ , C 1 ^- , C 2 , C 2 из первых четырёх уравнений в (3) и

3. Численный пример

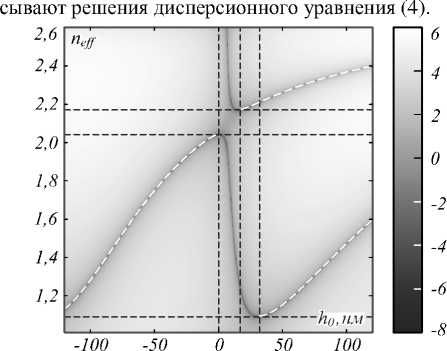
Расчёт зависимости константы распространения ПЭВ k_{x ,0} (или эффективного показателя преломления n eff = k x , ₀/ k 0 ) от какого-либо параметра у ФК может быть произведён «графически», то есть на основе анализа нулей графика функции |D( n ef , у )|, являющейся левой частью дисперсионного уравнения (4). Для понимания вида дисперсионных зависимостей h ₀ = h ₀( n_e ff ) на рис. 2 показано полутоновое изображение функции ln(| D ( n eff , h 0 )|), рассчитанной при следующих параметрах: X = 800 нм, е ₀ = 1, е 1 =7, е ₂ = 2,25, h 1 = 120 нм, h 2 =200 нм (рис. 2). Такие параметры использовались в работе авторов настоящей статьи [17] и были выбраны для последующего сравнения результатов расчёта. Линии минимумов на рис. 2 опи-

их подстановкой в пятое уравнение в следующем виде:

5 = cos ( kz ,1 [ h + h ])х х ik,0 cos ( kz,2h ) + kz,2 sin ( kz,2h ) + ikz,0 cos ( kz ,1 h0 ) + kz,1 sin ( kz,1 h0 )

+ sin ( kJ h0 + h1])x x kz2,1 cos ( kz,2 h2 )-ikz ,0 kz ,2 sin ( kz ,2 h2 ) ikz,0kz,1 cos ( kz,1 h0 ) + kz2,1 sin ( kz,1 h0 ) ’

где h ₀ = h ₀( k_{x ,0}) имеет вид (7). Таким образом, расчёт величины ^ по формуле (8) позволяет выбрать правильный знак перед первым слагаемым в правой части формулы (7).

Рис. 2. Полутоновое изображение функции ln(|D(n_e ff , h₀)|), где D(n_e ff , h₀) – левая часть дисперсионного уравнения (4). Пунктирными линиями показаны дисперсионные кривые, рассчитанные по формулам (7), (8)

Графики зависимостей эффективного показателя преломления ПЭВ n eff от величины h ₀ e [-120,120] нм, рассчитанные по формулам (7), (8) для двух мод соседних порядков ( m =0 и m = 1 в (7)), показаны пунктиром на рис. 2 и совпадают с линиями минимумов функции ln(| D ( n eff , h 0 )|). На основе приведённого в пункте 2 анализа можно заключить, что линии минимумов на рис. 2, которые не отмечены пунктиром, описывают решения дисперсионного уравнения, для которых мода фотонного кристалла является возрастающей при удалении от границы раздела. Горизонтальными точечными линиями на рис. 2 показаны границы фотонных запрещённых зон. Согласно рис. 2, вне запрещённых зон не существует волн с действительным значением n eff , имеющих вид плоской волны (2) при z >  h 0 и вид моды ФК при z <  h 0 . Отметим, что вне запрещённых зон значения h 0 , рассчитываемые по формуле (7), получаются комплексными. Вертикальными точечными линиями на рис. 2 показаны соответствующие границам запрещённых зон значения h ₀ =0 и h ₀ = 17 нм, а также значение h ₀ = 32 нм, соответствующее началу «двухмодового» режима, в котором для одного значения h ₀ существуют две ПЭВ с различными константами распространения.

Результаты расчётов по формулам (7), (8) (пунктирные линии на рис. 2) полностью совпали с графиками, представленными в работе [17]. Профиль поля ПЭВ при n eff = 1,44 и h 0 =–83 нм приведён на рис. 1 и также совпадает с профилем поля, представленным в указанной работе. Это подтверждает правильность полученных формул (4), (7), (8). Отметим, что в работе [17] и других известных работах не приведено законченных аналитических выражений для расчёта зависимостей h ₀ = h ₀( n_e ff ). В частности, в [17] значение h 0 = h ₀( n eff ) определялось через параметр ц = C 1 -/ C 1 ⁺ , который определялся численным расчётом.

Заключение

Рассмотрен вывод дисперсионного уравнения БПВ, распространяющейся вдоль границы раздела полубес-конечного одномерного фотонного кристалла и однородной среды. Дисперсионное уравнение решено относительно толщины верхнего слоя фотонного кристалла. Полученное аналитическое соотношение позволяет рассчитать зависимость константы распространения БПВ (эффективного показателя преломления) от толщины верхнего слоя фотонного кристалла. Указанное соотношение может быть использовано для расчёта интегрированных «на чипе» оптических элементов для БПВ с использованием метода эффективного показателя преломления.

Работа выполнена при поддержке гранта РФФИ 17-47-630323 (получение дисперсионного уравнения БПВ); гранта РНФ 14-19-00796 (получение и анализ выражения, описывающего зависимость константы распространения (эффективного показателя преломления) БПВ от толщины верхнего слоя фотонного кристалла) и Федерального агентства научных организаций (соглашение № 007-ГЗ/Ч3363/26) (расчет численного примера и его анализ).