О связи строения стационарных подгрупп группы графа и эффективности учёта симметрии при решении переборных задач структурного анализа

Графовые модели систем (ГМС) рассматриваются в качестве математических моделей объектов и процессов всё в большем числе прикладных областей. В связи с этим увеличивается значимость методов структурного анализа и возрастает актуальность повышения эффективности точного решения базовых задач структурного анализа. К ним относятся такие труднорешаемые (в том числе NP -полные) задачи, как различение ГМС (изоморфизм и изоморфное вложение), декомпозиция ГМС на неизоморфные фрагменты, анализ сходства ГМС (в первую очередь — поиск максимальных общих фрагментов) и другие.

Подходы к повышению эффективности решения переборных задач на графовых моделях многообразны, но наиболее интересны обладающие достаточной универсальностью. Можно выделить как минимум четыре широко используемых подхода: применение инвариантов ГМС и их частей; применение эвристик, учитывающих специфику исследуемой ГМС и специфику (семантику) задачи; применение методов форсирования поиска решения; учёт симметрии анализируемых ГМС. Методов учёта симметрии также предложено много. Может учитываться симметрия расположения вершин и более крупных фрагментов, сама симметрия может пониматься по-разному.

Мы рассмотрим точный учёт симметрии расположения вершин ГМС при реализации метода поиска с возвратом и его обобщений, когда частичное решение представляет собой некоторую последовательность вершин и/или рёбер ГМС. На основе подобных алгоритмов построено подавляющее большинство программных средств точного решения базовых задач структурного анализа для ГМС общего вида. Это направление исследований развивается давно и достаточно плодотворно, некоторые результаты приведены в [1–2].

Точный учёт симметрии подразумевает, что множество кандидатов для достройки частичного решения строится таким образом, что включает только по одному представителю каждой орбиты фиксатора или стабилизатора (в зависимости от решаемой задачи) вершин, уже присутствующих в частичном решении. Введём необходимые определения (даются по [3]).

Пусть задана ГМС в виде конечного обыкновенного графа G = (V,E) с числом вершин p и её группа автоморфизмов Aut(G). Фиксатор [pointwise stabilizer] подмножества вершин V 0 ⊂ V — подгруппа Aut(G,V0), оставляющая неподвижной каждую вершину множества V 0 , то есть Aut (G,V 0) = Пуск о Aut (G,v). Стабилизатор [setwise stabilizer] подмножества вершин V1 С V — подгруппа Aut[G,V 1], оставляющая множество V1 неподвижным, то есть Aut[G,V 1] = {g G Aut(G) : Vv G V 1[g(v) G V1 ]}. Орбита [orbit] вершины v G V — подмножество 0 (Aut (G), v) вершин графа G, которые могут быть отображены на вершину v: 0(Aut(G),v) = {vf : [3g G Aut(G) : g(v) = v]}.

Орбиты вершин относительно фик-сатора/стабилизатора определяются аналогично. Далее для краткости мы будем говорить просто об орбитах фиксато-ра/стабилизатора.

Для анализа симметрии на практике никогда не используется полная группа автоморфизмов графа (ГАГ), так как её порядок может быть очень велик (вплоть до факториала числа вершин). Используются различные порождающие множества (ПМ) ГАГ. Для полного описания ГАГ достаточно менее p автоморфизмов, но для эффективного решения большинства задач анализа ГАГ более удобно так называемое «сильное ПМ» мощностью не более чем p • ( p — 1) / 2 автоморфизмов.

Башней орбит фиксаторов графа G назовём корневое дерево FT ( G ), с каждым узлом которого, кроме корневого, ассоциирована вершина w графа G и фиксатор некоторого подмножества вершин G , включающее w . С корневым узлом вершина не ассоциирована и ассоциирован фиксатор пустого подмножества вершин, то есть сама Aut ( G ). Для каждой нетривиальной (содержащей более одной вершины) орбиты фиксатора любого узла существует единственный дочерний узел, ассоциированный с произвольной вершиной из этой орбиты, не ассоциированной ни с каким узлом на цепи от данного узла до корневого, и фиксатором Aut ( G,W ) множества вершин W , состоящим из этой вершины и вершин, ассоциированных со всеми узлами, лежащими на цепи от данного узла до корневого. Очевидно, с листьями дерева ассоциированы тождественные фиксаторы.

Для общей характеризации «симметричности» графа в терминах башни орбит фиксаторов используются интегральные показатели, называемые числами тождественной и нетождественной стабильности [4].

Подмножество вершин V + С V называется экстремальным подмножеством тождественной стабильности графа, если

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 справедливо

( Aut ( G,V ⁺ ) « E p )&( V v G V ⁺ : Aut ( G,V ⁺ \{ v } ) ^ E p ) .

Подмножество вершин V - С V называется экстремальным подмножеством нетождественной стабильности графа, если справедливо

( Aut ( G,V - ) ^ E p )&( V v G V \ V - :

Aut ( G,V ^- U { v } ) ^ E p ) .

Пусть П ⁺ и П - обозначают соответственно множество всех подмножеств V ⁺ и V - вершин графа G . Тогда ^ = min v + _{е П} + | V ⁺ 1 — число тождественной стабильности графа, а X = max v - _Е п - I V ^- | — число нетождественной стабильности графа. Для тождественного графа по определению ^ = 0 и X = — 1. Число тождественной стабильности графа представляет собой минимальную мощность подмножества вершин графа, относительно которого фиксатор группы автоморфизмов является тождественным, а число нетождественной стабильности графа представляет собой максимальную мощность подмножества вершин графа, относительно которого фиксатор группы автоморфизмов не является тождественным. Другими словами, минимальный уровень FT ( G ), на котором появляются листья, равен ( ^ + 1), а максимальный — ( x — s + 2), где s — число вершин, входящих в тривиальные орбиты фиксатора родительского узла листа и не ассоциированных с узлами-предками листа.

Рассмотрим транзитивный граф, изображённый на рис. 1. Башня орбит этого графа приведена на рис. 2.

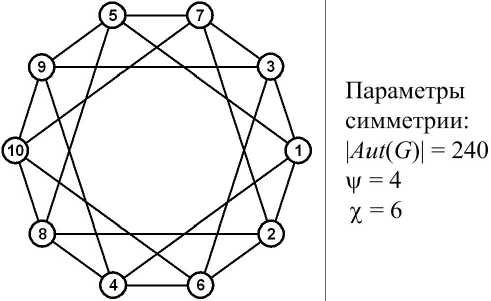
Рис. 1. Транзитивный граф, для которого будет построена башня орбит фиксаторов

Башня орбит стабилизаторов (корневое дерево ST (G)) определяется аналогич- но, но с тем отличием, что листом дерева может быть нетождественный стабилизатор, когда все вершины его нетривиальных орбит уже были ассоциированы с родительскими узлами.

Строение башен орбит может быть совершенно разным даже у похожих графов одного класса. Рассмотрим класс транзитивных графов степени 4 [3]. Отметим, что практическая значимость класса транзитивных графов очень высока, например, в качестве топологий вычислительных сред, в качестве моделей оптимальной связности при анализе надёжности сетей и т. д.

В этом классе присутствует очень интересное семейство (рис. 3) со сложным строением стационарных подгрупп (назовём его «сложным»).

Fix:       -

Orbits: (1,2,3,4,5,6,7,8,9,10)

Fix:

Orbits:

(4,5)(6,7)

j---------------------

Fix:

Orbits:

(3,4)(7,8)

j---------------------

Fix:

Orbits:

(3,4)(7,8) j---------------------

Fix:

Orbits:

(2,3)(8,9) 1---------------------

Fix:      4

Orbits: -

Fix:      3

Orbits: -

Fix:      3

Orbits: -

Fix:      6

Orbits: -

Fix:      7

Orbits: -

Fix:      7

Orbits: -

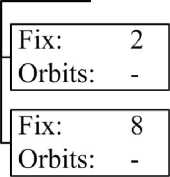
Рис. 2.

Пример башни орбит фиксаторов (Fix — фиксируемая вершина, Orbits — нетриви- альные орбиты фиксатора)

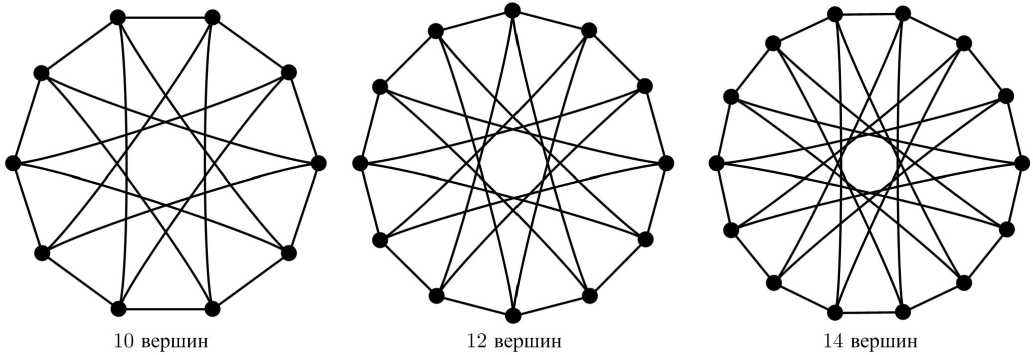
Рис. 3. Семейство транзитивных графов степени 4 (сложное)

У графов этого семейства ^ = р/ 2, а X = Р - 2 [3]. Поэтому учёт симметрии при фиксации частичного решения без дополнительных ограничений будет продолжаться до уровня р/ 2 (причём на всех ветвях!). А учёт симметрии без ограничений при стабилизации частичного решения может вообще потерять смысл.

Существуют в некотором смысле противоположные «вырожденные» семейства транзитивных графов с тождественным фиксатором вершины (полурегулярной группой), у которых ^ = 1, а х = 0. Но мы рассмотрим другое семейство («простое») того же класса транзитивных графов степени 4, представители которого приведены на рис. 4, то для него ^ = 3 и х = 3 (для стое» относительные, то есть только по отношению друг к другу и только в смысле строения башни орбит.

любого числа вершин ^ 10). Это семейство вполне отражает ситуацию в среднем. Отметим, что определения «сложное» и «про-

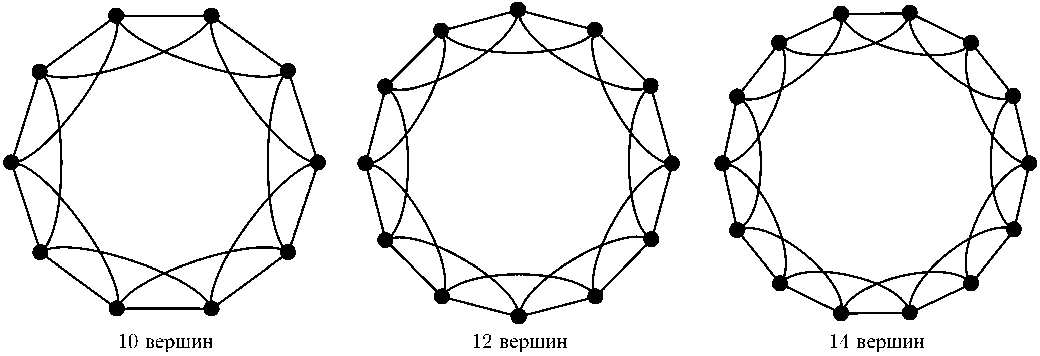
Рис. 4. Семейство транзитивных графов степени 4 (простое)

Рассмотрим вопрос трудоёмкости построения башни орбит, так как оценка времени построения башни орбит даёт верхнюю границу накладных расходов на учёт симметрии. К настоящему времени результаты, полученные в рамках вычислительной теории групп, позволяют выбирать различные подходы к алгоритмизации основных задач анализа ГАГ [5–7]. Некоторые давно развиваемые и широко используемые алгоритмические разработки свободно доступны: B.D. McKay, The nauty page au/ ∼ bdm); GAP System for Computational Discrete Algebra .

Авторами было реализовано четыре алгоритма построения башни орбит, из которых выбрано два лучших, имеющих несравнимые напрямую преимущества. Алгоритм 1 один раз строит сильное ПМ ГАГ, после чего использует перестройку ПМ методом Шрейера–Симса для поиска фиксаторов/стабилизаторов. Алгоритм 2 строит каждый фиксатор/стабилизатор независимо методом уточнения упорядоченных разбиений множества вершин графа (с нахождением не более p автоморфизмов). В табл. 1 приведены результаты построения башни орбит фиксаторов для сложного и простого семейства. Здесь и далее все замеры времени работы проводились на компьютере с процессором AMD Athlon 64 X2 4200+ и 1 ГБ оперативной памяти.

Ясно, что учёт симметрии как метод повышения эффективности решения дру- гих задач структурного анализа можно дополнительно оптимизировать в зависимости от решаемой задачи. Были реализованы алгоритмы установления факта изоморфного вложения пары графов и поиска максимального общего связного фрагмента пары графов по методологии монотонного расширения частичных решений (ММРЧР), предложенной Коховым В.А. и Грызуновым А.Б., а также некоторые другие переборные алгоритмы. Для повышения их эффективности Незнановым А.А. был реализован универсальный настраиваемый механизм учёта симметрии.

После реализации исследовательских версий алгоритмов и накопления статистических данных выяснилось, что пространство параметризации учёта симметрии весьма велико. Только основных параметров в итоге оказалось более восьми, среди которых:

• 1)    метод учёта симметрии, то есть манипуляции ПМ ГАГ (в настоящий момент реализовано три различных метода);

• 2)    вариант использования учёта симметрии (зависит от решаемой задачи);

• 3)    уровень дерева поиска, на котором директивно прекращается учёт симметрии;

• 4)    использование кэша орбит (зависит от решаемой задачи) [8];

• 5)    метод кэширования орбит (бинарное дерево, хэш-таблица и т. п.);

• 6)    объём памяти, резервируемый под кэш орбит.

Таблица 1

Время построения полной башни орбит фиксатора

Число вершин	Сложное семейство			Простое семейство
	Число узлов	Время (мс)		Число узлов	Время (мс)
		Алг. 1	Алг. 2		Алг. 1	Алг. 2
12	165	5	11	7	2	7
14	980	13	14	8	4	8
16	6852	73	60	9	5	7
18	54802	610	487	10	7	7
20	493207	6136	4737	11	10	8
22	4932052	70846	51315	12	12	8
24	54252558	896316	604997	13	17	9

Таблица 2

Эмпирический анализ алгоритма поиска МОСП для сложного семейства

Числа вершин 10–12	Без учёта симметрии		С учётом симметрии
	Время (мс) 382	Число узлов 197970	Время (мс) 40	Число узлов 42	ДВУС (%) 94,919
12–14	3097	1744153	42	76	46,589
14–16	28748	15067344	49	146	59,631
16–18	189379	95674410	68	310	72,277
18–20	1630707	776847730	103	678	86,808
20–22	—	—	206	1536	97,178
22–24	—	—	491	3451	97,408
24–26	—	—	1284	7779	97,766

Таблица 3

Эмпирический анализ алгоритма поиска МОСП для простого семейства

Числа вершин 10–12	Без учёта симметрии		С учётом симметрии
	Время (мс) 198	Число узлов 103795	Время (мс) 35	Число узлов 1000	ДВУС (%) 60,543
12–14	1158	600306	43	4630	31,824
14–16	7423	3654100	87	23617	14,896
16–18	39380	18067888	277	108852	5,286
18–20	199214	83500454	1239	479568	0,836
20–22	—	—	17428	6337745	0,194
22–24	—	—	90325	30750542	0,047
24–26	—	—	362730	112877665	0,015

Очевидно, что существуют оптимальные значения этих параметров для конкретных входных данных. Возникает вопрос: как алгоритм может приблизиться к этому оптимуму в автоматическом режиме, то есть без ручного задания дополнительных параметров? Ответ на этот вопрос разбивается на две части. Первая часть связана с применением алгоритмов анализа строения ГАГ. Действительно, можно относительно просто определить некоторые свойства стационар- ных подгрупп ГАГ и использовать полученную информацию для настройки учёта симметрии. Это является актуальным направлением дальнейших исследований. Вторая часть связана с использованием технических приёмов, не затрагивающих суть алгоритма. Среди них можно выделить следующие. 1. Применение адаптивных методов динамического программирования для исключения повторных вычислений орбит фиксатора/стабилизатора для одного и того же подмножества вершин [8].

• 2.    Cравнение относительных затрат времени и выигрыша от учёта симметрии на разных уровнях и ветвях дерева поиска для возможного отказа от учёта симметрии на некотором уровне/ветви.

• 3.    Создание нескольких версий алгоритма, которые могут заменяться друг на друга во время выполнения (например, при переходе с уровня на уровень дерева поиска).

• 4.    Распараллеливание как базового метода решения задачи, так и учёта симметрии (анализа подгрупп ГАГ).

Таким образом, не вызывает сомнений возможность дальнейшего повышения эффективности с одновременной специализацией механизма учёта симметрии.

В качестве модельного примера рассмотрим поиск максимального общего связного подграфа (МОСП) пары графов. Первый вариант алгоритма не использует каких-либо улучшений стандартной схемы ММРЧР. Второй вариант использует схему ММРЧР, дополненную учётом симметрии. Подчеркнём, что никаких других методов повышения эффективности в исследовательских вариантах алгоритмов не использовалось намеренно. Реализация алгоритма без средств сбора статистики, с использованием инвариантов, форсирования и т. п. средств заметно эффективнее. Учёт симметрии выполнен по схеме неограниченного кэширования орбит стабилизаторов. В качестве входных данных используем уже упомянутые ранее показательные семейства. Пары графов образуются как граф и последующий граф того же семейства.

В табл. 2 содержатся результаты выполнения алгоритмов для сложного семейства: время выполнения алгоритма («Время») и число узлов («Число узлов») в дереве поиска, а для варианта алгоритма с учётом симметрии дополнительно приведена доля времени, затраченного на учёт симметрии, от общего времени выполнения алгоритма («ДВУС»). В табл. 3 содержится аналогичная информация для простого семейства. Прочерки в таблицах — следствие резкого возрастания времени работы алгоритма при малой значимости получаемых данных.

Особо отметим асимптотику доли времени (рис. 5), затраченного на учёт симметрии. Для сложного семейства доля стремится к 100%, а для простого — к 0%. Но это не должно вызвать удивления после приведённой выше информации о высоте башен орбит, времени их построения, уменьшении числа узлов дерева поиска МОСП при использовании учёта симметрии.

Анализ табл. 2 и 3 (а также результатов других вычислительных экспериментов) позволяет сделать интересные выводы.

• 1.    Несомненно, учёт симметрии при обработке симметричных (в данном случае — транзитивных) ГМС полностью оправдан. Эффективность может повышаться не просто в несколько раз, а на много порядков.

• 2.    Поведение учёта симметрии (как компонента некоторого переборного алгоритма) может кардинально меняться в зависимости от исходных данных.

• 3.    Поведение учёта симметрии в основном определяется строением башни орбит стационарных подгрупп ГАГ.

• 4.    В большинстве случаев накладные расходы на учёт симметрии становятся пренебрежимо малыми с ростом размеров входных данных. Но существуют уникальные вкрапления графов с очень сложным строением ГАГ, где накладные расходы на учёт симметрии резко возрастают, однако это не мешает общему повышению эффективности.

Эти выводы подтверждаются объёмными вычислительными экспериментами, проведёнными в АСНИ «Graph Model Workshop» на различных классах ГМС (в том числе взвешенных). Исследовались наиболее показательные (обладающие представительными группами) семейства обыкновенных графов (сильнорегулярные, транзитивные, симметрические), а также практически значимые классы ГМС: полициклические молекулярные графы, регулярные топологии вычислительных сред и др. (всего более 147 000 ГМС). Учёт симметрии в области её применимости является действительно универсальным методом повышения эффективности решения переборных задач, но требует понимания её особенностей и подстройки параметров при применении.

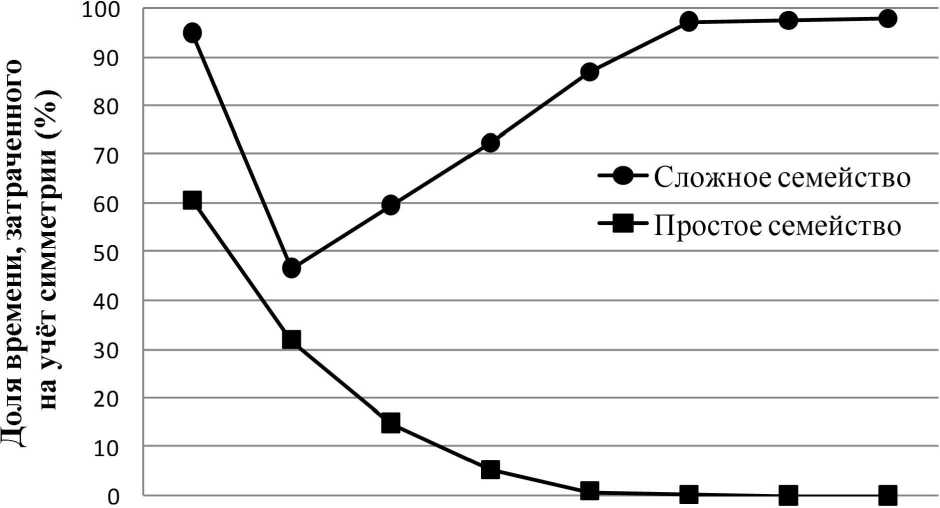
12-14   14-16   14-16   16-18   18-20   20-22   22-24   24-26

Рис. 5. Сравнение поведения учёта симметрии

В заключение заметим, что учёт симметрии зачастую полезен даже при решении задачи полиномиальной сложности. Это может происходить, например, в следующих случаях.

• 1.    Задача имеет полиномиальную сложность из-за особенности обрабатываемого класса ГМС. В этом случае и задача анализа симметрии скорее всего тоже будет полиномиальной. Так, это верно для деревьев [9].

• 2.    Задача является составной частью более крупной задачи, и учёт симметрии используется многократно. Это активно используется при проведении многоэтапных вычислительных экспериментов, например, при уточняющем многоэтапном поиске структурной информации [10].