О сводимости оптимальной проблемы моментов к парциальным в задачах управления многомерными линейными системами

Решение задач оптимального управления для многомерных динамических систем связано, как правило, с существенными затруднениями. В этих случаях находит применение принцип Сандерса [1], существо которого заключается в том, что многомерная система управления декомпозируется на парциальные подсистемы меньшей размерности так, чтобы решение задач оптимального управления для таких систем не представляло значительных затруднений. Получаемые таким образом частные решения затем принимаются в качестве начального или последующего (в рамках соответствующих итерационных процедур [1]) приближения для решения исходной задачи оптимального управления.

Если многомерная динамическая система является линейной и вполне управляемой, то ее декомпозиция по входам осуществляется с приведением к канонической форме управляемости с двусторонней связью, предложенной Луенберге-ром [2, 3]. Для линейной системы

dx

— = Ax + Bu (!) dt где X Е Rn - вектор переменных состояния, UЕ Rm - вектор управляющих параметров, A Е Rnхn — матрица динамики, B Е Rnхm - матрица входов, каноническая форма управляемости с двусторонней связью имеет вид dz                  m

-=- = F k x k + e n_k u k + Z D kj z j , k = 1, m , (2) dt                           j =1

( j * k )

где Z k Е R n^k - вектор переменных состояния k -й

m подсистемы ( Znt = n), enk = col(0>—,0J)ERnk, k=1

Fk =

0 n k -1

En_k -1

Е R n k ^х n k - матрица Фро

бениуса, в которой E n k -1 - единичная матрица соответствующего порядка, а ^ k = col ( a n k , a n k _{- 1}) - вектор коэффициентов характеристического многочлена, сопровождаемого матрицей F _k , а также

D kj =

^{0 (} n k ^-1)х n

d T kj

Rnk х n j                        v j – матрицы связей, а

d kj Е R n j - вектор коэффициентов связей; j = 1,2,..., m , d kk =^{- co1 (} a n k , a n _k -1 ) . Если вве-

сти

m вектор-функции f^ = Z Dkjzj k=1

, то парци-

альные системы (2) будут представляться в виде n_k -кратных интеграторов. Аналогичная декомпозиция возможна и для нелинейных систем уп-

dx равления ----= f (t, X, u) , если они допуска- dt

ют представление в таком виде:

dx

---= Ax + Bu + CT (t, x, u)     (3) dt где a (t, X, u) - вектор-функция “остаток” от f (t, X, u) после выделения в последней линейной части по x и u ; отметим, что в общем случае матрицы динамики и входов в (3) могут

зависеть от t . Соответствующий подход был рассмотрен в [4] с помощью итерационной процедуры синтеза решения задачи оптимальной переориентации космического аппарата в пространстве и при сведении последней к задачам оптимального управления по отдельным каналам ориентации.

1. ПОСТАНОВКА ЗАДАЧИ

где u ( т ) - оптимальное управление. В (7), (8) l T C = 1 и, h T ( . ) = l T ® ( t f , т ) B = [ Л ₁ o ( T )| ^ | Л m 0 ( т )] ,

|| h ( ' ) |_л" = L _p

f (|| й «) pt k p

V t 0                      V

1 <  p <^ ,

|| h OHt ) = max || h ( т ) ||_v , "      те[ 1 0 , t f ]

В связи с изложенным далее рассматриваются управляемые линейные системы такого вида:

d x

—— = Ax + Bu + f ( t ), dt

|| h ( т )|| _у - векторная норма ( V = 1,2, ^ )

1 ₊ 1 = 1

V Ц

Кроме того, предполагается, что для граничных

которые допускаю декомпозицию в прямую сумму парциальных подсистем вида (2):

dxr = Akxk + bkuk + fk(t) , k = 1, m , (5) dt где x = col (x1,...,xm)eRn , u = col (U1,...,um)eRm, матрицы динамики и входов имеют следующее устройство: A = diag {Ak}m, B = diag {bk}m, а пары {Ak, bk} имеют согласованные размеры при включении в состав (4) и являются вполне управляемыми для всех k = 1m, а f = col (ffm)e Rn (fk e Rnk) -’некоторая заданная вектор-функция (здесь и далее предполагается, что здесь f t = f k (t) ), с помощью которой могут моделироваться перекрестные связи как в (2) или (3) между подсистемами (5) системы (4).

Для граничных условий:

x ( t ₀) = x ⁰ ; x ( t f- ) = x ^f , (6) задача управления (4), (6) на заданном интервале [ t o , t f ] - двухточечная граничная задача, сводящаяся при минимизации функционалов типа нормы в L q ^[ t 0 , t f ] ( q = 1,2, ^ ) к решению оптимальной проблемы моментов в L _p , где

1 1 1

--1— = 1. Моментные равенства здесь имеют pq вид: f f Ф (tf, т) Bu (т) d т = c , где Ф(tf, т) - пе-

J t о         f реходная матрица системы (4), а вектор c вычисляется так: C = xf - Ф( tf, tо) x0 - P Ф( tf,т) f (т) dт.

• 0

Решение указанной проблемы моментов с помощью принципа максимума Н.Н. Красовского [5, 6] сводится к последовательному решению следующих двух задач:

А 0 ); P 0 = min|| l ^T Ф ( t, , ■ ) B || L ⁾ = || h 0 < . )|| L ⁾ (7) l ^T c =1                         p                 p

Б ₀) max

| u (<’ = -

L q P 0

f h 0 ( т ) u ( t ) d r = f h 0 ( т ) u ( т ) dr = 1 , (8)

условий (6) выполняется условие || c || _V > 0 .

Соответственно, для граничных условий парциальных подсистем (5), задаваемых исходя из условий (6):

x_k ( 1 0 ) = x k ; ^x k ⁽ t f ) = x^{f f} , ⁽ k = 1, m ) ⁽9) можно также рассматривать парциальные задачи оптимального управления для (5), (9) с функционалами типа нормы J k = H ^uk OH L _q и также сформулировать соответствующие проблемы моментов в L _p , которые сво дятся к решению следующих пар задач ( k = 1, m ):

A k ) л k = min П ^ T ^ф k ⁽ t f , •) b k П _L p =

5 1 Ck =1

kk

= ^min H ⁵ k g k ⁽.⁾h

5 T Ck =1 kk

^| L _p = ^|| g k 0 ⁽ ■ ^)|| L _p ;

tf

Б k )      ^max 1 f g k 0 ^{( т )} u_k ^{( т )} d ^т =

^|| u k ('^ L q ⁼ n k 1 0

tf

= f g k 0 ^{( т )} u k ^{( т ) d т} = ¹ ,        ⁽¹¹⁾

t ₀

где uk (т) - оптимальное управление, Фk (tf, т) -переходные матрицы для парциальных подсистем (5), а векторы ck вычисляются по форму- лам: Ck = xkf - 0k (tf, t0) xk - P 0k (tf,т) fk (т) dт ,

^J t 0

|| C k | | _V >  0 ; если же C k = 0 , то управление k -й системой (5) не требуется, то есть и_к ( т ) = 0 Vт e [ 1 0 , t f ] , поскольку в этом случае граничные условия (9) удовлетворяются автоматически. Отметим также, что g k 0 ( т ) = 5 T0 g k ( т ) , 5 k ^T0 C k = 1 , и по определению системы (4) и ее парциальных подсистем (5):

Ф ⁽ t f , ^{т ) B} = ^diag ^{{ 0} k ⁽ t f , ^{т )} b k ^} m = diag { g k ( т )} m .

2. РЕШЕНИЯ ЗАДАЧ ПО СВЕДЕНИЮ ОПТИМАЛЬНОЙ ПРОБЛЕМЫ МОМЕНТОВ В L _p К ПАРЦИАЛЬНЫМ ПРОБЛЕМАМ МОМЕНТОВ

решение задачи на минимум (10), где ^ _{к 0} = р _k G _kk с _к ,

В настоящей статье рассматривается решение задач сведения проблемы моментов А₀ ), Б д ) (7), (8) к пар циал ьным проблемам моментов А _к ), Б _к ), к = 1, m , (10), (11) и построению на их основе решения задачи оптимального управления для (4), (6). В общем случае имеется девять вариантов постановок таких задач с учетом того, что p = 1,2, то и v = 1,2, то . Очевидно, что не все из возможных вариантов постановок задач являются равноценными в аспекте решения прикладных задач. Тем не менее, далее представлены результаты по всем возможным вариантам, в том числе для случаев, когда оптимальная проблема моментов А ₀ ), Б₀) (7), (8) не сводится к парциальным А _k ), Б _k ) (10), (11), но получаемые при этом результаты не исключают построения на их основе вполне эффективных итерационных процедур для решения задачи оптимального управления рассматриваемого класса для систем вида (4), (5). Итак, далее в следующем порядке: p = 2,1, то , рассмотрим решения задач по сведению оптимальной проблемы моментов в L _p к парциальным, отвечающим задачам оптимального управления для (5), (9), и возможности построения на основе их решений для задачи (7), (8).

Вариант L ₂ ( p = 2 ). Вначале рассмотрим решения задач (7), (8) и (10), (11) в случае p, v = 2 . Для этого введем _n представление l = col ( l ,..., l _m ) , где l n k ^G К. , и с учетом структуры переходной матрицы для системы (4) задачу (7) перепишем в виде

tf

Gkk = J 8к(т)gT(т)dт ,    рк =(cTGkk1 ск Г1   и t0

^T Ск = 1. При этом также получим л к = Рк и u<т> = 7Т ^кТ0§к(т) = CTG§к(т), Vtg [t0,tf]. (12) рк                                     J

Сравнивая решения задач Б 0 ) и Б к ) ус тано ^вим, что ^hk 0 ⁽ т ) = а к^дк 0 ⁽ 0 , ¹ к 0 = ^а к £ к 0 , к = 1, m .

mm  m

Поскольку Z ^l T0 ^С к = Z ^a к ^ м ^с к = Z ^a к = ¹ , ^то к =1            к =1                к =1

m

P 0 = Z' к =1

2_2

,^а к ^Л к . Задача р ₀

m

2_2

а к Л к имеет

m

Z а к =1 ^к -¹

к = 1

m

-2    _-2

решение: а к = Л к Z Л j , к = 1, m , а также j=1

m

P0 = Z

^Л к

V к =1     7

В конечном счете, имеет место:

P 0 = min ||[ l 1^T g 1⁽ - )| - I l m g m С)]^ = m -г

Z l k c = 1

к = 1

= !![ 1 T g 1 ( - )! - | l I c g m OlH^ .

Следовательно, р 0

t f _m

= J Z h k ²0^{( T )} d ^т ’ ^{а из (8)}

1 0 ^{k =1}

получим:

t fm

JZ h k 0 ^{( t )} u к ^{( т )} d ^т = ¹ ;

1 0 k =

t fm

J Z ^йк ^{( т )} d ⁷:.

,, к =1                Po

й _к ( т ) = и к ( т ) , к = 1, m , ^Vte ^[ t 0 , t f ^] , то есть решение задачи оптимального управления для системы (4) или, что то же самое, для решения задач А 0 ) и Б 0 ) в L 2 вполне достаточно решить задачи меньшей размерности А _k ) и Б _k ) (также в L 2 ) для подсистем (5), оптимальное управление для которых (12) также будет оптимальным управлением и для системы (4).

Задачи управления для случаев v = 1, ^ (при p = q = 2 ), по-видимому, не представляют особой ценности для решения прикладных задач и, с другой стороны, в общем случае они могут быть решены, как правило, только с помощью численных методов. В связи с этим следует отметить важное значение решение такого класса прикладных задач оптимального управления (1), (3), сводящихся к оптимальной проблеме моментов в L j с функционалами типа нормы !! U ( - )!!,-

L то ⁽ Ц = 1,2, то ).

Вариант L 1 ( p = 1 ) . Тогда задачу (7) следует переписать так:

tf

P 0 =

Из (10) следует, что Л _к

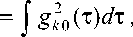
а в усло- t0

min

m

Z l T с = 1

к = 1

!![ 1 1^T g 1 ( - )!-! l , T g m ( - >]Il L '1 ^> =

вии максимума (11) имеет место:

= !![ l T0 g 1 ( - )! - ! l ,T« g m ( - )]II ^, _I ^, ₁ ^, .

t f                      1

J^{[ и} к ^{( т )]} 2 d Т = — . Здесь д к 0 ⁽ т ) = ^ T g k СО ^- t ,                    ^Л к

Здесь

P 0

t f

=J

t 0

m

Z! Кк 0( т )r к=1

1 V

d т , а из (8)

tf m следует j E hk0 (т)йk (т)dТ = 1 при условии, что

1 0 ^k =1

max || ( т )|| „=— . Последнее означает, что здесь

1E[ t о, tf ]

оптимальные управления ограничены по норме, а именно: при ц = 2 ограничения будут накладываться на модуль вектора управлений, то есть m1

max E u²_k ( т ) <— ; при ц = ^ - на каждую ком-

Т t о, tf] к=1

поненту вектора управлений в отдельности, то есть здесь max | uk (т) | <   , Vк = 1, m . Если же t о, tf ]

ц = 1, то ограничивается суммарная “скорость”’ m1

расходов управления: max E i u k ^{( T )|} <^_.

TE [to’tf] k=1

Вначале рассмотрим случай ц = 2 . Тогда

в

t f _m

(7), (8): P o = j E h k ²o ( T )

t к = 1 t o L-

² d т ,

m max E uk (т)

^{ТЕ [} t o , t f ^] k = 1

^, P o

Из условия максимума в (8)

m

E ^a k ^л k = ^P o . Здесь имеет место: Л k = P _o , k =1

k = 1, m , и, стало быть, оптимальные управления (14) будут оптимальными и для задачи (4), (6) с функционалом || U ( • )|| L ) .

t _f

Если ц = 1 , то в (7), (8) P o = j max | Z^g k (т) | dT

1-k < m to m1

и max E | u _k ( t) | - —. Из условия максимума

ТЕ [to,tf] k=1

(8) здесь имеет место:

tf m                        m1

maxjE|zkogk(т)|^k(t)|dT=1; E|uk(t)|et, uk (•) , k_!                                        k=!

t _o k =1

что эквивалентно простейшей задаче оптимального распределения заданного ресурса [7] для каждого момента времени ТЕ [ t o , t f ] . Решение этой задачи в силу линейности ее целевой функции является очевидным.

Вводя функцию ko (t) = arg max 11Togk (t) |, 1-k < m получим в рассматриваемом случае следующую программу оптимального управления

( V k = 1, m ):

^{u ( T )}

¹     h o^{( T )}

^P o H h o ^{( t )||} 2

или u _k (t) =

¹     h k o^{( T )}

^P o  H h o ^{( t )||} 2

k = 1, m , Vte [ t o , t f ] .

Соответственно, в задаче (10)

t f 1

Л k = fl gk o(T)| dT и | Uk (t)| < —, t                             " k to а из условия максимума (11) получим uk(Т) = — signgko(t), Vte[to,tf]. лk

Из сравнения (13) и (14) видно, что u _k ( т ) не является оптимальным управлением для задачи (4), (6). Степень неоптимальности управлений (14) в сравнении с (13) можно оценить, если подставить u k ( т ) в (5) вместо U ( т ) . Если она мала, то u k ( т ) можно использовать как начальное приближение для решения задачи (4), (6) с функционалом J = || U ( • )||^ .

В случае Ц = ⁰⁰ из (7), (8) получим

U i k ( Т ) = — sign h k o ( т ) , V k = 1, m , а из (10), (11) ^P o                          m

- (14). При этом lko = akCko, где E ak = 1, и k=1

~ A   rEign l^k о g k ^{( Т )}

Uk (Т) = ^Po      ko o,

k = k o ( ^T );

, Vte [ t o , t f ] . ^k ^ W,

Из сравнения этой программы с (14) видно, что здесь, как и в случае ц = 2 , управление (14) не является оптимальным для двухточечной граничной задачи (4), (6) с функционалом J = || u ( • )||™ . -•-'co

Вариант L ^ ( p = ^ ). Предваряя рассмотрения еще одного решения задачи сведения оптимальной проблемы моментов к парциальным, отметим, что выше установлено: решения задач (10), (11) доставляют решение и для задачи (7), (8) только в случаях p, v = 2 ( q,Ц= 2 ) и p ,v = 1 ( q , ц=^ ). В иных рассмотренных вариантах постановок задач (7), (8), когда v ^ p , получаемые решения для парциальных задач (10), (11) можно рассматривать только как соответствующие приближения. То же самое справедливо в общем случае и для варианта p = ^ , в котором при v = ^ решение задачи (10) будет иметь вид:

^л k

= mm

< i c = 1 L

max | ^ T g k ( t )| ^{te [} t o , t f ^]

= ^| C To g k ^{( T} ,_k ^)|, ¹ <  i_k <  r k <~

где m k ( t ) = C _iT_o g _k ( t ) — функция, наименее уклоняющаяся от нуля [8], а ^Т i_k ^{Е [} t o , t f ^] - точки

максимума |ю = ( т ) | . Здесь из условия максимума

(11) при

f              1

J |ик (т)| dт = — ,                Л к имеет место:

tf j юк (т)u= (т)dт = 1. Таким образом, отсюда сле- дует, что здесь оптимальное управление будет 5 -импульсным, а именно:

u k ^{( т} )

0,

^А i k ^{5 ( т}"^т i k )’

^v^ ^[ t о , t f 1\ I k ;

^т = ^т i _k ^e I k ,    ⁽¹⁵⁾

где It = {т, }. ;—, и, соответственно, полный k 1 ik ’Ч =1,rk rk                 1

импульс управления будет равен V | Аi | = —, ______               i k =1 k л k а значения А- , Ц = 1,Г, , отыскиваются с уче-ik kk том граничных условий (9).

Если теперь в (7) принять I T с = = tt k , где

m

V ttk = 1, и lk = аk£k0 ( k = 1,m ), то в силу k = 1

свойств функций ю= (т) тогда выполняются сле дующие условия: Ро = «1Л 1 = ■■■ = tt m Л m . Отсю да получаем tt k =-Р0- , k = 1m , то есть Ро -л k среднее гармоническое {лk }k=fm • Соответственно, оптимальное управление (15) для подсистем (5) является таковым и для системы (4).

ЗАКЛЮЧЕНИЕ

Основной результат в настоящей статье заключается в следующем: проблема моментов (7),

(8) в Lp , p = 1,2,^, для задачи оптимального управления (4), (6) в общем случае сводится к решению проблем моментов для парциальных подсистем (5), (6) только тогда, когда имеет место V = p для показателя векторной нормы ||(-)||v . Если V ^ p, то решения парциальных задач оптимального управления (5), (9) с соответствующими функционалами типа нормы в т / 1 1 , X

L q ( — + — = 1 ) не доставляют решения задачи pq

(4), (6), хотя в том случае, когда степень их нео-птимальности является вполне допустимой, они могут быть приняты не только как соответствующее приближение в процедуре реализации принципа Сандерса, но и в качестве приближенно оптимального управления для исходной многомерной системы (4), (6).