О сжигании распыленного жидкого топлива

Полидисперсность системы капель распылённого жидкого топлива можно учитывать на основании кинетического уравнения для функции распределения частиц по радиусам f(r_s,t), аналогично рассмотренным в работах [1, 2]. Новым в таком подходе является то, что эволюция функции распределения зависит от кинетики процесса горения отдельной частицы, а не выбирается произвольным образом, что встречается в ряде работ.

Решение кинетического уравнения возможно при представлении скорости горения единичной капли в виде произведения двух функций O(r _s ) и m(t):

W(r _s ,t) = ^ = Q (r _s )xw(t), (1) где W (r _s , t) — скорость горения единичной капли; r s – радиус капли; t – время.

Тогда функция распределения частиц по радиусам также представляется в виде произведения двух функций, зависящих только от радиуса, и только от времени. Это позволяет получить функцию распределения для автомодельных режимов горения в виде [2]

ffeO = A Q"1(rs)exp[—a J Q-1(rs)drs] x

x exp [a J w(t)dt]. (2)

Конкретный вид функций Q (r _s ) и w(t) вытекает из рассмотрения кинетики горения единичной капли. Для определения скорости горения использован кондуктивный перенос теплоты на испарение и горение капли жидкого топлива, предложенный в работе [3].

Капли топлива впрыснуты в газ, содержащий окислитель, с температурой среды Тср.0 выше температуры воспламенения, имеют сферическую форму, их массовая концентрация мала. В зоне горения (фронте пламени) весь окислитель расходуется и его концентрация равна нулю, так же как расходуются все пары топлива. Можно считать, что зона горения очень мала и имеет радиус фронта пламени rf [3].

В такой постановке задачи можно принять, что в пространстве между каплей и фронтом горения ( r s <  r <  r f ) находятся пары топлива, которые нагреваются от температуры поверхности капли T s до температуры воспламенения, которая при горении быстро даёт температуру фронта пламени T f , т. е. можно считать, что нагрев топлива происходит до температуры T f . За фронтом пламени ( r >  r f ) происходит кондуктивная передача теплоты на нагрев среды, окружающей каплю, в которой находится окислитель и продукты горения, разбавленные инертным газом.

Из уравнений баланса энергии для областей ( r s <  r <  r f ) и ( r >  r f ) получается выражение для расчета массовой скорости горения, из которого получена скорость изменения радиуса капли. Её можно представить в виде произведения двух функций:

W(rs,t) = Q(rs) x m(t) , где Q(rs) = -;

' s

":'    ;. Л1 ■ :7^Ih

+ In [1 + С2(Т/~Тср) ],(3)

PTc2 L Qr-L-c1(T/-Ts)J’ где λ1, λ2 – коэффициенты тепловодности среды до и после фронта горения; c1, c2 – удельная теплоемкость среды до и после фронта горения; ρ1 – плотность жидкого топлива; L1 – теплота испарения топлива; QR – теплота сгорания, rs – радиус капли; Тf – температура фронта горения; Тs – температура поверхности капли.

В условиях интенсивного горения температура поверхности капли Ts близка к температуре кипения [3]. Температура Tf незначительно отличается от теоретической Ta и может быть определена через нее, т. е. её можно считать известной и постоянной, поскольку она изменяется в процессе горения слабо. При постоянных средних коэффициентах теплопроводности и удельной теплоемкости временная часть скорости горения ω(t) будет зависеть только от температуры среды Tср.

Подстановка в (2) конкретного вида функции Ω( r s ) из (3) даёт

f(r_s, t) = A r _s exp [- ^ r _s ² ] exp [а / w(t)dt], (4) где а - константа разделения; A - константа интегрирования.

Соотношение (4) позволяет получить в дальнейшем усредненные характеристики полидис-персной системы: среднюю поверхность, объем, температуру среды и т. д. На основании (4) доля несгоревшего топлива y ( t ), как отношение несгоревшей массы капель M k ( t ) к их начальной массе M k 0 получается в виде

y(t) = ^^ = exP [а £ ®⁽t⁾^t]. (5)

Из уравнения (5) получим дифференциальное уравнение для расчёта доли несгоревшего к данному моменту времени топлива y

^ = -am(t)y. (6)

Для его решения необходимо связать температурный напор ( T f - T с _р), входящий в m(t), с долей несгоревшего топлива y , что получается из уравнения теплового баланса системы капель. Предполагается, что горение паров топлива идёт до образования двуокиси углерода, поэтому в нагреваемой среде содержится кислород и азот воздуха совместно с продуктами горения. Теплота реакции горения расходуется на испарение капель топлива, подогрев паров топлива от температуры поверхности капель T_s до температуры фронта горения T f с добавлением теплоты, поступающей от продуктов сгорания в окружающую среду из фронта пламени.

Уравнение теплового баланса принимает вид:

(aM _k c _k + aM _N2 c _N2 + М п- с п. ⁾    =

= - -^ [Q _fi - L - _{С 1} (7 > - T_s) - С пг (7 > - 7 ср )], (7) где a - коэффициент избытка воздуха; M k , M_N ^ , M _пг, M _Т – массы кислорода, азота, продуктов сгорания и топлива соответственно; c k , c _N2 , c _пг -теплоемкости кислорода, азота и продуктов сгорания.

Вводя обозначения

М то _r   ОШ   ш п

И MN2, cпр mN2 ck + шт Спг, где mT, mk, mпг – молекулярные массы топлива, кислорода и продуктов горения, с учетом, что горят пары топлива, уравнение (7) для доли несгоревшего топлива y приводится к виду

[1 + и ^-^К’

= ;^N; le+^с пг (⁷ > -^т с, М.             (8)

где β = Q_R – L – c _п1( T f – T_s ) и c _п1 – теплоемкость паров топлива в области радиуса r ( r_s< r < r f ).

Формула (8) связывает искомую температуру T _cp с долей несгоревшего топлива y . Определив Т _ср из (8) и упростив полученное выражение, на основании (3) и (6) получим дифференциальное уравнение для степени выгорания топлива:

• -■^ + а (а * + d * )y - ad * y ² = 0.             (9)

где введены обозначения:

а = ²Г²⁽^^/2) ; а * = 3^in [i + £ 1 (т - 7)];

Г^²           Рт ^с1    ^L I ^{v ; s}

• d* =----²---; т^З" - средний начальный ра-

• Cn2Ptmno

диус частиц; Г(3/2) – неполная гамма-функция.

Уравнение (9) решается в конечном виде. На рис. 1 и 2 представлены выгорание паров топлива во времени (см. рис. 1) и степень выгорания по длине камеры сгорания в одномерном стацио-

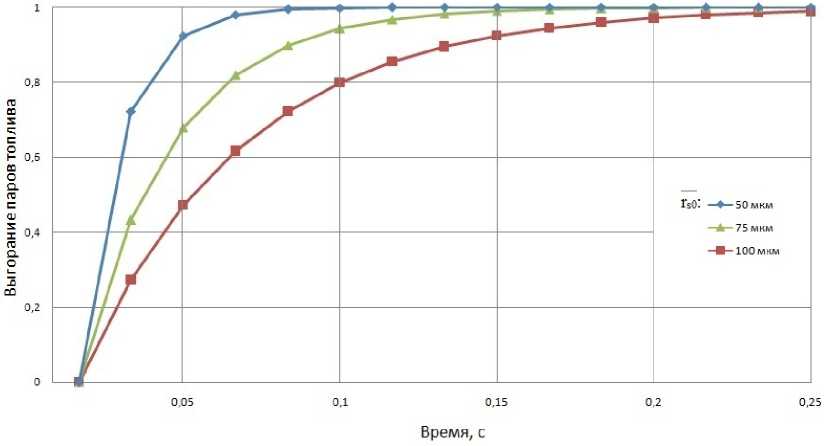
Рис. 1. Выгорание паров топлива во времени

Голдобин Ю.М., Кузнецов П.С.

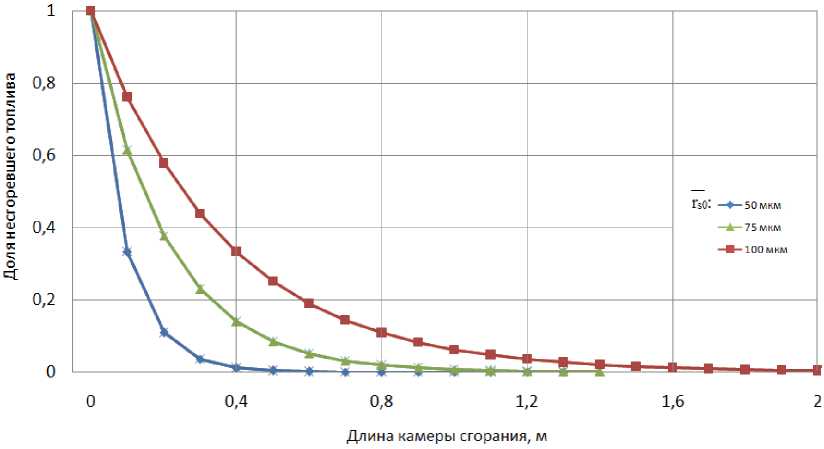
Рис. 2. Изменение доли несгоревшего топлива по длине камеры сгорания

на рном пото ке при с ред н е й с корос ти д в и ж ени я капель 6 м/с (см. р и с. 2) . Увели ч ен и е ск о р о с т и в ед ёт к ув еличе н ию д ли ны факе л а . За в исим ос ти р а с с чита ны д л я диз ел ьного топли в а с о с л ед ую щими характеристиками: L = 189 кДж /кг, T f = 1973 К, T s = 426 К, λ 1 = 0,06 Вт/м∙к, λ 2 = 0 , 08 Вт/м∙к.

Выводы

• 1.    Д л я пров е де н ия ра с чё тов не обх од им о экс пе рим ен та л ь но опре де лить ил и з а датьс я с ре дн им начальным размером частиц т^.

• 2.    Предлагаемая методика р а с чё та а де кв атно о п ис ыв ает в ыгора ние пол и д и сп ерс ного т опл и в а по длине ка м ер с гора ни я и м ож е т бы ть ре ком е ндова на д л я пре д в ари те л ь ной о ц е нк и д л и ны ка м е р при сж и га н и и ра з личны х жид ки х топ л и в .

• 3.    Методику расчёта можно уточнить, учитывая внешний теплообмен к стенкам камеры сгорания.