О течении в окрестности плоскости симметрии холодного треугольного крыла при стремлении показателя адиабаты к единице

Характер течения в пространственном ламинарном пограничном слое на плоском холодном треугольном крыле, обтекаемом потоком при больших числах Маха на режиме сильного вязконевязкого взаимодействия, существенно зависит от угла стреловидности передней кромки крыла в и от величины показателя адиабаты y = Cp/Cv (Cp и Cv — соответственно удельные теплоемкости при постоянном давлении и постоянном объеме) [1, 2]. Крыло считается холодным, если температура его поверхности Tw мала по сравнению с температурой торможения T0 набегающего потока. Известно [3], что для каждого конечного значения параметра е = 7 ~ 1 существует критический угол стреловидности крыла β ∗ . При углах больше критического в пограничном слое на всем крыле реализуется область докритического течения, в которой возмущения распространяются от плоскости симметрии крыла вплоть до передних кромок, так как течение в ней является в среднем «дозвуковым» [1]. При углах стреловидности меньше критического в пограничном слое возникают области как закритического, так и докритического течений. В областях закритического течения, расположенных около передних кромок, возмущения не распространяются вверх по потоку, так как поток в них является в среднем «сверхзвуковым» [1]. Как показали численные исследования, при обтекании холодных треугольных крыльев с удлинением s = ctg в = O (1) безразмерный размер области докритического течения существенно уменьшается [3, 4], то есть, за исключением узкой области в окрестности плоскости симметрии, практически на всем крыле реализуется режим закритическо-го течения. Определение параметров в этой области при малых значениях ε из решения уравнений в частных производных с помощью конечно- разностных методов представляет определенные сложности.

Рассматривается обтекание полубесконечной треугольной пластики на режиме сильного вязконевязкого взаимодействия. Предполагается, что температура поверхности T _w мала по сравнению с температурой торможения T 0 набегающего потока и параметр ε асимптотически стремится к нулю. Газ считается совершенным с постоянными значениями C _p и C _v . Вязкость линейно зависит от температуры ц 0 Jц ^ = C ^ T 0 JT ^ , где C ^ = const, а индекс го обозначает параметры в невозмущенном потоке. Компоненты вектора скорости u ⁰ ,v ⁰ ,w ⁰ направлены соответственно вдоль осей x ⁰ ,y ⁰ ,z ⁰ декартовой системы координат, начало которой расположено в вершине крыла с полууглом ш о (рис. 1). Удлинение крыла s = tg ш о . В невозмущенном потоке u _∞ — скорость, ρ _∞ — плотность и g _∞ — энтальпия торможения стремятся к постоянным значениям, когда число Маха М ∞ → ∞ . Тогда p ∞ — давление, a ∞ — скорость звука и T _∞ — температура стремятся к нулю.

Рис. 1

Согласно гиперзвуковой теории малых возмущений [5] при М _L ^ 1 и безразмерной толщине ламинарного пограничного слоя 5 ^ 1 в случае выполнения предположения о сильном скачке М _L 5 ^ 1 индуцированное давление имеет порядок p 0 — р ^ и ^ 5 2 . Статическая энтальпия в пограничном слое h 0 — и L / 2. Для плотности газа в пограничном слое имеем оценку:

р 0 _— Р 0 h ^ ρ ∞   p ∞ h

_— P ^ uU 2    a L    _{— 5} 2 -1

p l   ⁽ Y ^- 1) u L

∂u0    ∂ р и dx° — dy° (ц

ρ∞ δ2 u2∞   μ0u∞ eL — 52 L2 ,

Для оценки толщины δ , приравнивая порядки главных вязких и инерционных членов, получаем ∂u ⁰ ∂y ⁰

5 — e ¹ / 4 Re 1 / ⁴ . (2)

Здесь Re ° = p _L u _L L/^ 0 — число Рейнольдса, ц 0 — динамический коэффициент вязкости, вычисленный при температуре T 0 , L — характерный размер, который при рассмотрении обтекания полу-бесконечной пластики из конечных результатов выпадает.

Рассматривается случай, когда плотность газа в пограничном слое мала по сравнению с его плотностью в невозмущенном потоке р ⁰ /р ™ ^ 1 и, следовательно, e ^ 5 ² . Из уравнения количества движения вдоль оси z ⁰ оценим величину поперечной компоненты скорости w ⁰ , которая создается в пограничном слое перепадом давления вдоль оси z ⁰ :

р ° и ° ^aw + р ° v °     + р ° w ° dw o =

∂x ⁰         ∂y ⁰         ∂z ⁰

- dp ° + d / ° dw ° \ (3) ∂z ⁰ ∂y ^{0 μ} ∂y ⁰

Если удлинение крыла s достаточно велико, то оценку можно получить из равенства порядков величин следующих членов уравнения (3):

° ° dw ° _— dp °    р ™ 5 ² u ^ w ° _— р ™ 5 ² и L

^ρ ∂x ⁰ ∂z ^{0 ,} εL           sL ^,

— - es ^{- 1} .                (4)

u ⁰

В рассматриваемом случае

(р ° w ° dw °/dz °)(dp °/dz °)-1 - e/s 2, и следовательно, для удлинений крыла s ^ ут конвективным членом ρ0 w0 ∂w0/∂z0 в уравнении (3) можно пренебречь. Заметим, что вне пограничного слоя для рассматриваемого случая 5/s ^ 1 согласно «теории полос» этот компонент скорости имеет порядок w° — ul52/s ^ uLe/s [6].

Заметим, что другой предельный случай реализуется для малых удлинений s . Оценка для w ⁰ тогда следует из условия равенства членов:

Причем продольные конвективные члены в уравнении (3) оказываются малыми при условии ( р ° и ° dw ° /dx ° )( р ° w ° dw ° /dz ° ) ^{- 1} ^ 1, то есть при s ^ V e . Уравнения пограничного слоя в этом случае вырождаются — выподают члены, содержащие производные по продольной координате x ⁰ .

Общий случай, когда все члены имеют одинаковый порядок, реализуется при удлинениях крыла s — eTe , и при этом сохраняется оценка для компоненты скорости поперечного течения (5) — w ° /u _l — e ¹ / ² .

Далее рассматриваются крылья с удлинением s = O (1) ^ e ¹ / ² , и при выполнении предположения М _L 5 ^ 1 для определения индуцированного давления, создаваемого толщиной вытеснения, можно использовать приближенную формулу «касательного клина» [5].

Согласно обычным оценкам для ламинарного пограничного слоя в гиперзвуковом потоке [2, 5] и учитывая (1), (2), (4), вводятся безразмерные автомодельные (по оси x ⁰ ) переменные и преобразование А.А. Дородницына:

А x° = Lx, y° = L5x3/4 С —, z° = Lsxz, ρ р ° = р™и L52 x 112 p* (z), р ° = р™5 2 e-1 x-1 / 2 р (X,z),

Ц ° = ц ° ц ⁽ X,z ) , g ° = 1 ^и L g ⁽ X,z ) , ^и ° = ^и ™ ^{и (} X,z ) , ²                            (6)

v ° = ul5s 1 x 1 /4 р 1 x x fv* (X,z) - suX - sxJ^ - ew^ ^ , 4      dx dz w ° = uLew (X,z), 5° = L5x3 /4 5* (z),

5 = e ¹ 1 ⁴ s ¹ 1 4 Re ^{- 1} / ⁴ .

В переменных (6) система уравнений пространственного пограничного слоя сводится к двумерной, зависящей от λ и z , так как продольная координата выпадает из краевой задачи.

Для учета особенностей поведения функций течения в случае e ^ 1 в окрестности передних кромок вводятся переменные, которые не являются автомодельными (по оси z ) в окрестности этих кромок даже при наличии здесь областей с закри-тическим режимом течения:

^П = _V 2 y (1 ^X - z 2 ) " / 2 ' ^{p (} z ’ = ^ ^{T T z} 2 '

Д( z ) = (1 - z 2 ) - ³ / ⁴ 5 * ,             (7)

° ° dw ° _— dp ° р ™ 5 ² ( w ° ) ² _— р ^ и L 5 ² w °

^ρ    ∂z ⁰    ∂z ^{0 ,}   εsL         sL u ∞

-

e ¹ 1 ²

-XX    w - «иг ) dn + ,    v*    , 1 .

p               dz   ^2 y (1 - z ² ) 1 1 ² J

Система уравнений пространственного пограничного слоя и граничные условия на холодной треугольной пластинке с учетом (6), (7) принимают вид f = (ew — suz )(1 — z 2) p-1,

∂u ∂u       sε fdz + vdn =  2(1 + e) p(g u

— e ² w ² ) x

/ 1 + z ²     1 — z ² dp ) d ² u

2          p dz dn ² ,

∂w ∂w fdz + vdn

—    —r— ( g — u ² — e ² w 2 ) x

2(1+ e ) p^vy             '

z +

1 — z2 dp    d2 w p ∂z ∂η2 ,

„dig    dg    d / 1 dg   1 — ad ( u ² + e ² w ² ) )

∂z    ∂η   ∂η σ∂η σ ∂η ,

dv            z   ssu    du dw 1 — dn = (ew-suz)_ — I _—,,_+edz) —

∞

—,        - ( g — u ² — e ² w ²) dn,

V20+ e_Р Г^У        ' ^h

p =

^{2 + e Г}|(1 + z ² )A

(a d A I ²

^{— z (1 — z} >  db

■

n = 0 : u = w = v = g = 0 ,

n ^ ж : u ^ 1 w ^ 0 g ^ 1 .

Здесь σ — число Прандтля. Система уравнения (8) существенно отличается от соответствующей системы [3] тем, что при предельном переходе e ^ 0 в данной системе толщина вытеснения уже не обращается в ноль. Решение краевой задачи (8), определяющее течение в пограничном слое на всем крыле, зависит в общем случае от параметров s , а и e = y — 1. Переходя в (8) к пределу e = 0, получаем

1 — z2 du    du p ∂z    ∂η

_∂ 2 _u

∂η ^{2 ,}

П = 0 : u = w = v = g = 0 , П ^ ж : u ^ 1 , w ^ 0 , g ^ 1 .

Систему (9) можно рассматривать как систему уравнений для определения главных членов разложения функций течения в степенные ряды по параметру ε . Эта система разделяется, так как в ней функции u , g , v , p и A зависят только от параметров s и σ и не зависят от поперечной компоненты скорости w , и этим она существенно отличается от общего случая, описываемого системой (8). Уравнение для компоненты скорости w является линейным с нулевыми краевыми условиями, и его решение определяется после нахождения указанных выше функций. Учитывая, что коэффициент при производной по координате z в уравнениях переноса в системе (9) пропорционален z име-няет знак только в плоскости симметрии крыла ( z = 0), то, следовательно, реализуется течение с плавным стеканием к данной плоскости, и на каждой половине крыла направление параболич-ности системы (9) сохраняется. Так как градиент давления в плоскости z = 0 равен нулю в силу симметричности течения, то для w в плоскости симметрии получается обыкновенное дифференциальное уравнение с решением w ( n,z = 0) = 0 [7]. Аналогичные результаты получены в [8] при рассмотрении ламинарного пограничного слоя на конусе при малых углах атаки в сверхзвуковом потоке и в [9] при исследовании обтекания крыльев специальной формы, обеспечивающей малые градиенты давления.

На передних кромках крыла z = ± 1 система (9) вырождается в две системы обыкновенных дифференциальных уравнений. В случае a = 1 решения для последних можно выразить через решение задачи Блазиуса [4, 10].

При исследовании течений в областях с закри-тическим режимом можно рассматривать течение около одной из передних кромок, например, z = 1 и ввести вместо (7) автомодельные переменные [4]:

1 — z ² dg    dg    д Г 1 dg 1 — a du ²

p ∂z    ∂η   ∂η σ ∂η σ ∂η

П а =

_V 2 Y (1 — z ) 1 / 2 ’ p ⁽ z ⁾⁼          ' ’

∂v ∂η

-suz ²

su ∂u

(T ^— sz^j

z ²

A( z ) = (1 — z ) ^{- 3} 1 ⁴ 5 e ,            (10)

p

v a

∞

^A= V 2 p P ^g u ^{2 )} dⁿ, 0

—z [( ew — suz ) d^ a + ,      v '      , 1 .

pa [           dz     ^ 2(1+ e )(1 — z )1 1 / 2 J

p = Г 3(1 + z2)A — z(1 — z2) dT 1 , 4

1 — z2 dwdw p ∂z∂η

—!(g - u2) (z +1—^2 ddp) + |2w, 2 p                p dzdn

Тогда в области закритического течения, в которой функции течения зависят от координаты П а (( u = u a ( П а ), w = w a ( П а ), v = v a ( n a ) , g = g a ( n a )), в случае ее существования при z k ^ z ^ 1 получаем систему обыкновенных дифференциальных уравнений [4].

Значение координаты z k перехода от закрити-

ческого режима течения к докритическому определяется в случае обтекания полубесконечной треугольной пластики из условия обращения в ноль

интеграла [1, 11], который в автомодельных переменных (10) имеет вид

I —

П/              22 2

ε            g a - u ² _a - ε ² w _a ²

2 u a sin( w 0 — w 1 ) — ew a cos( w 0

— w 1 )

—ga + ua + e2waj dna =0,

_ tg(w0 — w 1) Zk —.

tg w 0

Здесь угол ω 1 отсчитывается от передней кром-кис z — 1, а функции течения определяются из решения системы обыкновенных дифференциальных уравнений.

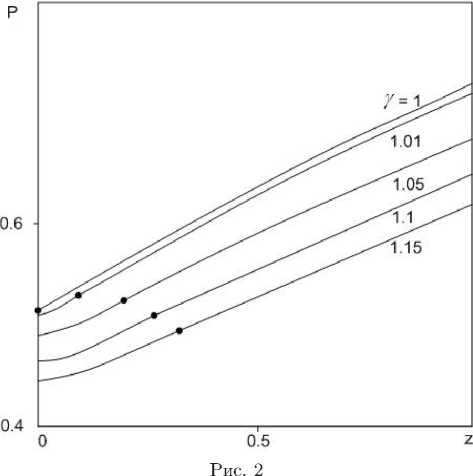
Система уравнений (8) решалась конечноразностным методом, изложенным в [9]. Расчеты проведены для случая s — 1, ст — 1 и Y — 1; 1 , 01; 1 , 05; 1 , 1;1 , 15. На рис. 2 представлено распределение давления по размаху крыла для различных γ . Точками обозначены координаты перехода от закритического к докритическому режиму течения. На рис. 3 представлено распределение индуцированного давления p в автомодельных переменных (10). В области докритического течения (область между звездочкой и плоскостью симметрий крыла) функции давления изменяются наиболее сильно. Согласно приведенным данным при уменьшении параметра γ координата перехода сдвигается к плоскости симметрии крыла, и, следовательно, размер области докритического течения уменьшается. При y — 1 область докри-тического течения исчезла.

Для исследования поведения функций течения в пограничном слое в окрестности плоскости симметрии крыла предполагается, что имеют место следующие разложения по ε :

и — u оо ( п ) + U 01 ( п ) e + и 02 ( п ) e ² + и 03 ( п ) e ³ +

+( и 10 < п ) + и 11 ( п ) e + и 12 < п ) e ² + ... ) z * ² +

+( и 20 ( п ) + и 21 ( п ) e + ... ) z * ⁴ + O ( e ⁴ ,e ³ z * ² ,e ² z * 4 ) , g — H 00 ( п ) + H 01 ( п ) e + H 02 ( п ) e ² + H 03 ( п ) e 3 +

^{+ ( H} 10 ⁽ п ) ^{+ H} 11 ⁽ п ) ^{e + H} 12 ⁽ п ) ^e 2 ⁺ ... ) ^z * 2 ⁺

+ ( H 20 ( п ) + H 21 ( п ) e + ... ) z * ⁴ + O ( e ⁴ ,e ³ z * ² ,e ² z * 4 ) , v — v 00 ( п ) + v 01 ( п ) e + V 02 ( п ) e ² + v 03 ( п ) e 3 +

+ ( v ю( п ) + v 11 ( п ) e + v 12 ( п ) e ² + ... ) z * ² +

+( v 20 ( п )+ v 21 ( п ) e + ... ) z * ⁴ + O ( e ⁴ ,e ³ z * ² ,e ² z * 4 ) , (12) w — ( w 00 ( п )+ w 01 ( п ) e + w 02 ( п ) e ² + w 03 < п ) e ³ + ... ) z * +

+( w 10 ( п ) + w 11 ( п ) e + w 12 ( п ) e ² + ... ) z * ³ +

+( w 20 ( п ) + w 21 ( п ) e + ... ) z * ⁵ + O ( e ⁴ z * ,e ³ z * ³ ,e ² z * 5 ) , A — A 00 ( п ) + ^д 01 ( п ) e + A 02 ( п ) e ² + A 03 ( п ) e ³ +

+(A xq ( п ) + A_n( п ) e + A 12 ( п ) e ² + ... ) z * ² +

^{+ (A} 20 ⁽ п ) ^{+ A} 21 ⁽ п ) ^{e +} ... ) ^z * 4 ⁺ O ^{( e} 4 ^,e 3 ^z * ^{2 ,e 2 z} * ^{4 )} ,

P — P 00 ( п ) + P 01 ( п ) e + p 02 ( п ) e ² + p 03 ( п ) e ³ +

+( P ю( п ) + P 11 ( п ) e + p 12 ( п ) e ² + ... ) z * ² +

+( P 20 ( п ) + P 21 ( п ) e + ... ) z * ⁴ + O ( e ⁴ ,e ³ z * ² ,e ² z * ⁴ ) .

После постановки разложений (12) в систему уравнений и краевые условия (8), собирая члены одного порядка по степеням ε и z , получаем соответствующие краевые задачи. Все эти системы являются системами обыкновенных дифференциальных уравнений. Для всех систем, кроме C 00 ^ 1, краевые условия нулевые.

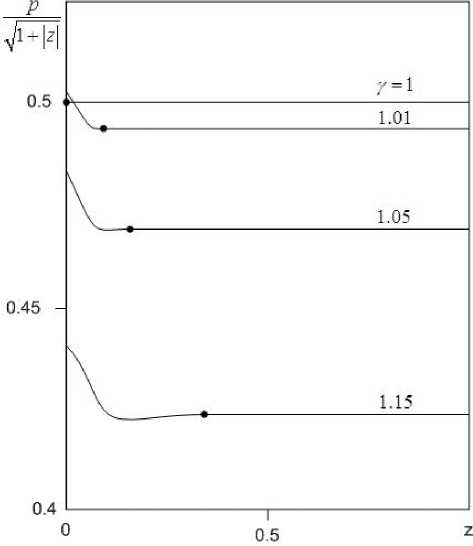
Рис. 3

Система C 00 ~ 1 и её решение:

du 00     d ² u 00

⁰⁰ dη dη ²

(13) ,

dH 0 ₀ _ 1 d ² H ₀₀    1 — ст d ² и 00

^{v 00} dη σ dη ² σ   dη ²

△ 00 ^_

dv 00 _ _ su 00 dn       4 p 00 ’

V² p 00

∞

I ( H 00

^_ u 00 ) dn,

Р 00 _(|) ² Д

Уравнение для w 00 отделяется, но оно зависит от p 10 из системы C 10 :

v ^dH 00 + v ^dH 10   2 ^su 00 H 10 _

¹⁰ dη ⁰⁰ dη        p 00

_ 1 d ² H 10 _ 2 1  ст d ² ( u 00 u 10 )

σ dη ² σ     dη ²

dv 10 _ _ su 00 / 1 _ Р 10 A + 7 su 10

dn 4 Р 00 V     Р 00)   4 Р 00 ’

Д 10 _

∞

~x=—    ^{( H} 10 ^{_ 2 u} 00 ^u 10) ^{_ ( H} 00 ^{_ u} 00) ~— dn,

2 p 00                                        p 00

dw 00 v 00

dη

su 00

---w00 _ p00

_ — f 2 p 00

1 + 2 РЮ- p00

■ ) * ⁽ H ^{00 _} u 00 ) ⁺ d_n 200 • ⁽¹⁴⁾

Р 10 ^_ о ^Д 00 ^(3Д 00 ^{_ 5Д} 10 ) • 8

Из системы (15) можно найти p 10 и замкнуть систему C 00 ~ 1, тогда из решения уравнения (14)

Граничные условия:

n _ 0 : u 00 _ v 00 _ H 00 _ w 00 _ 0 ,

П   ж. : u 00 ^ 1 , H 00 ^ 1 , w 00 ^ 0 •

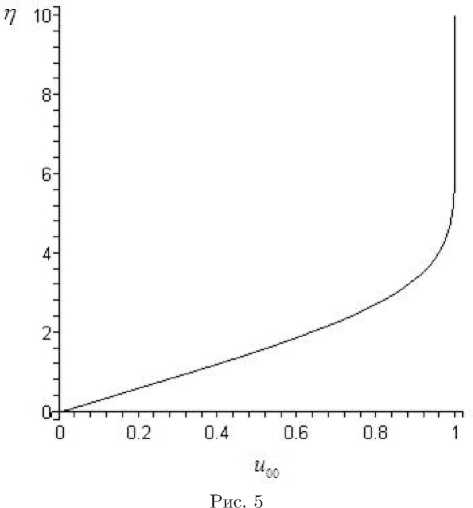
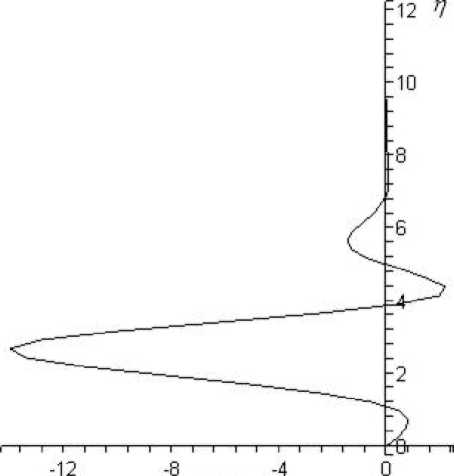
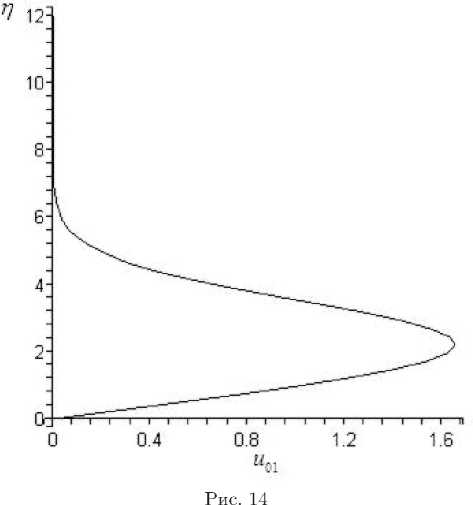
В качестве примера на рис. 4, 5 приведены компоненты скорости v 00 ( n ) и u 00 ( n ), полученные при решении системы уравнений пограничного слоя на треугольном крыле (13) при ст _ 1 и s _ 1. Поскольку ст _ 1, профиль энтальпии H 00 ( n ) точно совпадает с профилем u ₀₀ ( n ). В результате решения определяются следующие значения коэффициентов разложения: p 00 _ 0 , 498, Д 00 ⁼ 0 , 941. Согласно данным на рис. 5 видно, что верхней границе пограничного слоя соответствует координата n — 6 , 2. Уравнение (14) можно решить только после решения части системы C ю ~ z ² .

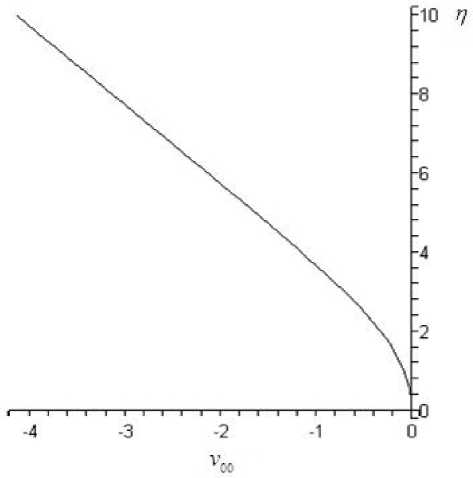
Рис. 4

определяется w 00 .

Уравнение для w 10 отделяется, но оно зависит от p 20 из системы C 20 ~ z 4 :

v dw 00 + v dw 10

10 dη 00 dη

s p00

x ( u 00 ( 1 + — ) _ u 10 ) w 00 _ 3 u 00 w 10 _ p 00

___L [ ₂ f 2 p 20 _ f p 10 ^Л

² p 001 у p 00     \p 00

( H 00 - u ² ₀₀ ) -

^{_ ( H} 00 ^{_ u} 00 ) f ² p 10 ^ ⁺ p 00

⁺ f ^{1 + 2}~—^{( H} 10 ^{_ 2 u} 00 ^u 10 ) ^_ p 00

f 1 + 2 p ¹⁰) ( H 00 _ u 00 ) p 00

Граничные условия:

/ p 10 Al, d 2 w 10

I p 00) J ⁺ dn ² ’

Система C ю ~ z ² и её решение:

v du 00 + v du 10

10 dη 00 dη

2 su 00 u 10 p 00

d ² u 10 dη ²

n _ 0 : u 10 _ v 10 _ H10 _ w 10 _ 0, n ^ ж : u 10 ^ 0, H10 ^ 0, w 10 ^ 0 •

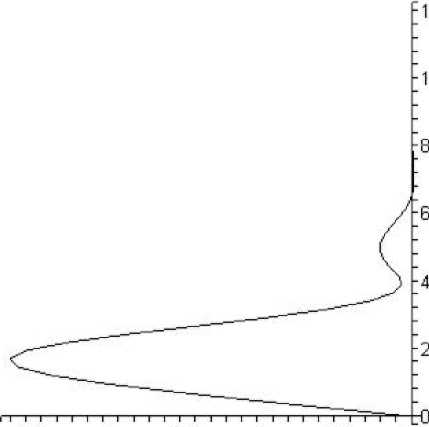
В качестве примера на рис. 6, 7, 8 приведены профили скорости v ₁₀ ( n ) и u ₁₀ ( n ) и производной по z

поперечной скорости w 00 ( n ), полученные при решении уравнений пограничного слоя на треугольном крыле (14) и (14) при ст = 1 и s = 1. В результате решения определяются p 10 = 0 , 28, Д 10 = - 0 , 0108.

1 d ² H 20    1 - ст d 2 (2 u 00 u 20 + u 10 )

σ dη ² σ         dη ²

dv 20 = 15 s 0 u 20 _— sp 10

dn      ⁴ P 00      4 p 00

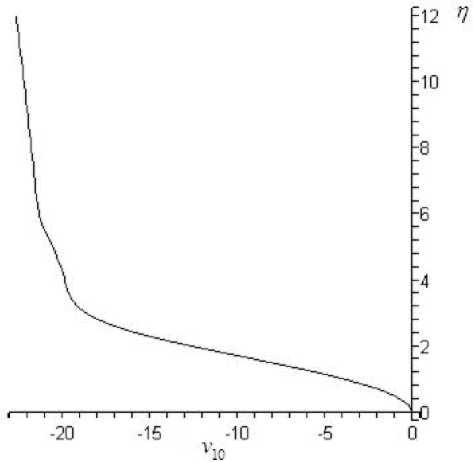
Рис. 6

■2.5       -2       -1.5       -1        -0.5        0

Рис. 7

Система C 20 ∼ z ⁴ и её решение:

v du оо ₊ v du io ₊ v du 20 _— 4 su 00 u 20 +

20 dη 10 dη 00 dηp su10        p10                 d2 u20

+2        1 +      u00 — u 10 = , ? , p00         p00

v dH 00 + v dH 10 + v dH 20   ^ su 00 H 20 +

20 dη 10 dη 00 dηp

+2HL [Л + EK) „00 - n„1 = p00

9 su 10 _— su 00

4p 00

,

∞

^Д 20 = “7=-- H 20 ^{— 2 u} 00 ^u 20 ^{— u} 10 ^—

2 p 00

— ( H10 — 2 u 00 u 10)”—+ p00

+( H 00 — u 00 ) ( — p + ( p ¹⁰ Й1 dn, ⁰⁰      p 00      p 00

p 20 = Т7[6^(11Д 10 ^{— 13Д} 20 ^)Д 00 ^{+ (ЗД} 00 ^{— 5Д} 10 ^{) 2} ] .

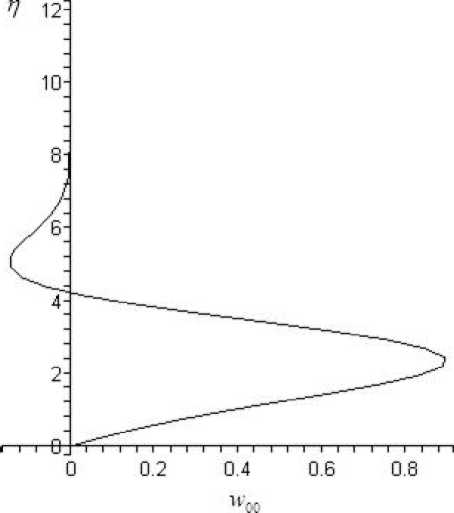
Рис. 8

Граничные условия:

n = 0 : u 20 = v 20 = H 20 = 0 ,

П • ^ : u 20 ^ 0 , H 20 ^ 0 .

Из решения системы (17) можно найти p 20 иза-мкнуть систему C 10 ∼ z ² , тогда из краевой задачи (16) определяется w 10 .

Уравнение для w 20 для краткости не приведено, но оно отделяется и зависит от p 30 из системы C 30 ∼ z ⁶ .

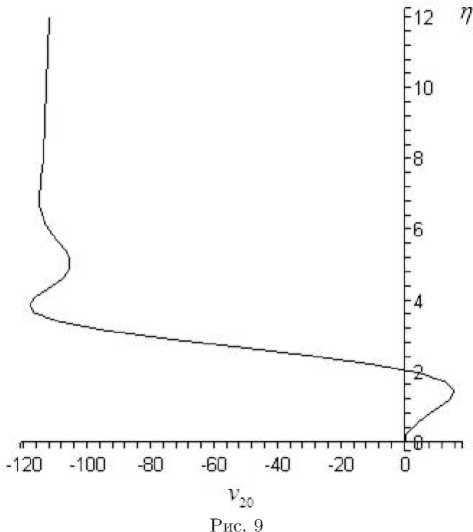
В качестве примера на рис. 9, 10, 11 приведены профили скорости v 20 ( n ), u 20 ( n ) и w 10 ( П ), полученные при решении уравнений пограничного слоя на треугольном крыле при ст = 1 и s = 1. В результате определяются коэффициенты p 20 = 0 , 33, Д 20 = — 0 , 921.

М2С

Рис. 10

Используя полученные значения коэффициентов, можно построить следующее координатное разложение p = 0 , 498 + 0 , 28 z ² + 0 , 33 z 4 , соответствующее e = 0.

Процедуру нахождения решений и замыкания систем уравнений представлена на рис. 12.

Учитывая [4], указанное разложение применимо в первом приближении для значений координаты z < z k и 0 , 8921 s ¹ д/ ё при числе о = 1.

Далее рассматриваются разложения по степеням ε .

Система C 01 ∼ ε и её решение:

du 00 du 01 s                 d ² u 01

" ⁰¹ W⁺ v ⁰⁰ "ПТ - 4⁽ H ⁰⁰ - “ оо > = "ПьТ • ⁽¹⁸⁾

^dH 00      ^dH 01 _ ¹ d ^{2 H} 01 Д - ^{od 2 (} u 00 u 01 )

⁰¹ dη ⁰⁰ dη σ dη ² σ      dη ²

dv 01 +  1 w = - su 01 + su 00 P 01

dn P 00          4 p 00      4 p 20 ’

△ 01

V2 p 00

∞

( H 01 - 2 u 00 u 01 ) -

- ⁽ H 00 - ^u 00 ) f^ ⁺ p ⁰¹ ) dⁿ, 2    p 00

(2Д 00 Д 01 +0 , 5Д 20 ) .

p 01 =

(I)2

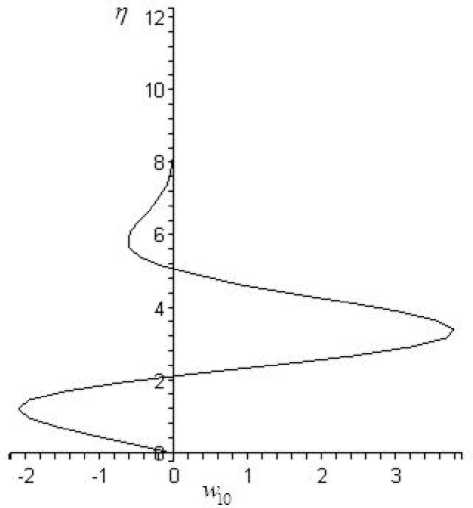
Рис. 11

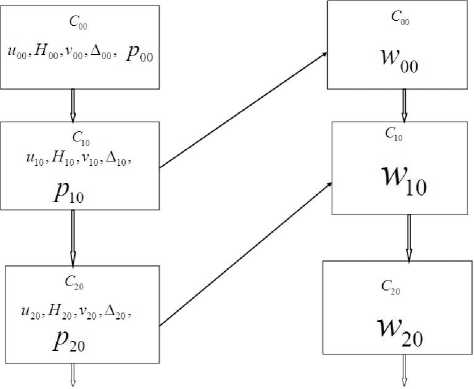
Рис. 12. Процедура нахождения решений и замыкание системы уравнений.

Граничные условия:

n = 0 : u 01 = v 01 = H 01 = 0 , у ^ ж : u ₀₁ ^ 0 , H ₀₁ ^ 0 .

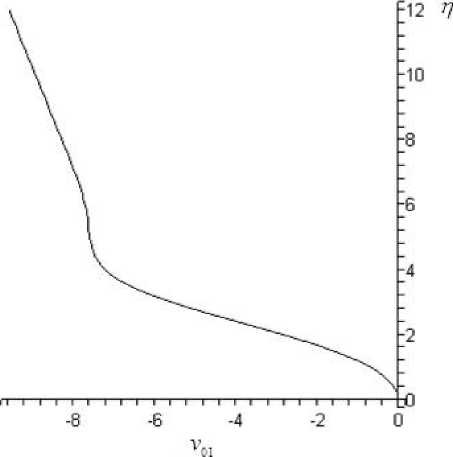
Рис. 13

Граничные условия:

n = 0 : w 01 = 0 ,

П ^ ж : w 01 ^ 0 .

В качестве примера на рис. 13, 14 приведены профили скорости v 01 ( n ) и u 01 ( n ), полученные при решении системы уравнений пограничного слоя на треугольном крыле при ст = 1 и s = 1. В результате решения найдено: p 01 = — 0 , 32, А 01 = — 3 , 436.

Система C 11

∼ εz ² и её решение:

p 00

u 10 w 00

p 01

su 01 + su 00--- p00

du 01

du 10

su 00 u 11 +

du 11

+ v ^du 00 + v ^du 01 + v ^du 10 + v ^du 11 =

¹¹ dη ¹⁰ dη ⁰¹ dη ⁰⁰ dη

= 2 p — [2 (⁽ H 10 ^{— 2} u 00 u 10 ) ^{— (} H 00

u 00)—) + p 00

^{+ (} H 00

2 A ( 1 , o P 10 M ^u ^U^ p 00 J J

+

d ² u 11 dη ^{2 ,}

p 00

H 10 w 00

p 01

su 01 + su 00--- p00

— su 00 H 11 +

Из решения системы (18) метр p 01 . Уравнение для w 01

зависит от p 11 из системы C 11 ∼ εz ² .

можно найти пара-отделяется, но оно

p 00

w 00

p 01

s 0 ^u 01 ⁺ s 0 ^u 00       ^w 00

p 00

dw 00

+ v 01—;— dη

dw 01

+ v 00—;— dη

— 1 L p^ — 2 p 00 p 00

s 0 u 00 w 01 +

p 10 p 01

)^{( H 00}

p 00

^u 20 ^{) +}

+ (1 + 2---(H01 — 2u00 u01) — p00

( 1 + 2 p ¹⁰) ( H 00

p 00

u 20 ) & + 1)} + dd^

dH 00

+ v 11—, --+ v 10

dη

1 d ² H 11

dH 01      dH 10

dη ⁰¹ dη

dH

+ v 00  - dη

σ dη ²

σ

ст d ² ( u 00 u 11 + u 01 u 10 )

dη ²

,

I v ¹¹ + -^[12 w 10 — 7 su 11 + su 01

dn    4 p 00

6 w 00 +

p 11      p 01 p 10

+su 00---+ 2—2— + p00 p2

⁺ ~— s ⁽7 u 10 ^{— u} 00 ) p 00

— p ¹⁰ (4 w 00 + su 01 )] = 0 , p 00

A 11

V² p 00

∞

j^[( H 11 ^{— 2 u} 00 ^u 11 ^{— 2 u} 01 ^u 10 ) ^—

^{+      (} H 10 ^{— 2 u} 00 ^u 10 )

2 p 00

+

~—⁽ H 01 ^{— 2 u} 00 ^u 01 ⁾⁺ p 00

p^ + 2 ^P ^- ^{P -2} + 1 5 ^) ( H 00 — u 00 )1 dn, p 00 p ₀₀      2 p 00

p 11 =   [А 00 (6А 01 — 10A_u)+

+А 01 (6А 00

10A 10 ) ⁺ A 00 ⁽3A 00

Граничные условия:

5A 1q )] .

n = 0 : u 11 = v 11 = H11 = 0, n ^ ж : u 11 ^ 0, H 11 ^ 0.

Из системы (20) можно найти p 11 и замкнуть систему C 01 ∼ ε , тогда из (19) определяется w 01 .

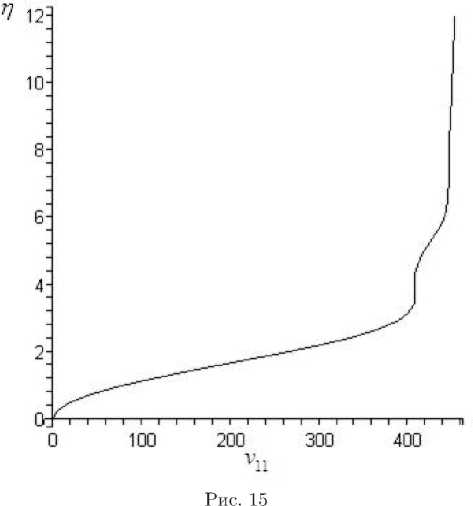
В качестве примера на рис. 15, 16, 17 приведены профили скорости v 11 ( n ), u 11 ( n ) и w 01 ( n ), полученные при решении уравнений пограничного слоя на треугольном крыле при ст = 1 и s = 1. В результате определяются p 11 = 2 , 1, Ац = — 3 , 37.

△ 02 =

V² p 00

∞

( H 02 - 2 u 00 u 02 - u ² ₀₁ ) -

f Z ⁺ ~— ^{( H} 01 ^{— 2 u} 00 ^u 01 ^{) +}

2 p 00

^p 02       ^p 01 ² . ^p 01 . ³

+ (H00 — u 00)--+ —  + -— + - p 00     p 00/     2 p 00   8

p 02 = f 4 ^ [2^ 00 ^ 02 ⁺ △ 21 ⁺ A 00 A 01 ] ,

p 00

w 01

p 01

su 02 — (w 00 — su 01)--- p00

dη

,

-su 00

+ w 00

p 02      p 01

---+  -- w 00 + p00     p00

p 01

su 01 + su 00      w 01

p 00

su 00 w 02   +

+ v 02

dw 00

dη

+ v 01

dw 01

dη

+ v 00

dw 02

dη

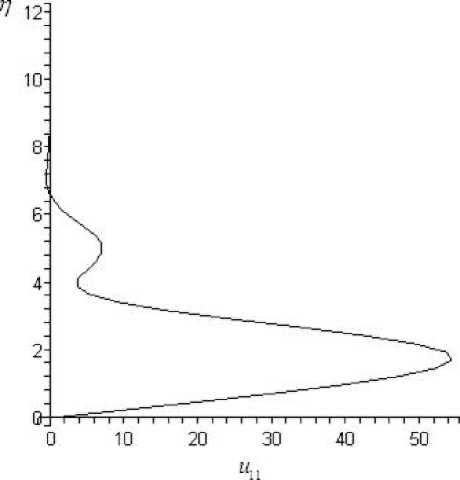
Рис. 16

2 p 00

p 12

p 00

p 11 p 01

p 2 ₀₀

+

^{X [(} H 02 ^{— 2 u} 00 ^u 02 ^{— u} 01 ) ^{+ (} H 00 ^{— u} 00 ) ^X

X f p02 + f p01 A p00     p00

+ ^p 01 + 1

p 00

f ^p 21 + Л [2 f ^p 1! — ^{p 1} p l) ( h 00 — u 2 )+ p 00             p 00      p ²₀₀              ⁰⁰

X

Система C 02 ~ е ² и её решение:

du 00       du 01       du 02

02 dη 01 dη 00 dη

-д ---^[( H 01 ^{— 2} u 00 u 01 ) — f l + ^01 A ⁽ H 00 ^—u 20 ^{)+    02} ,

4 P 00                   \    P 00/               dn ²

dH 00 v 02 dη

+ v dH 01 ₊ v dH 02

01 dη 00 dη

1 d ² H 02    1 — ad 2 (2 u 00 u 02 + u 01 )

σ dη ²       σ         dη ²

p 10         d ² w 02

⁺⁽ H 01 ^{— 2 u} 00 ^u 01)   ^{1 + 2}— I f +—, 9

p 00          dη ²

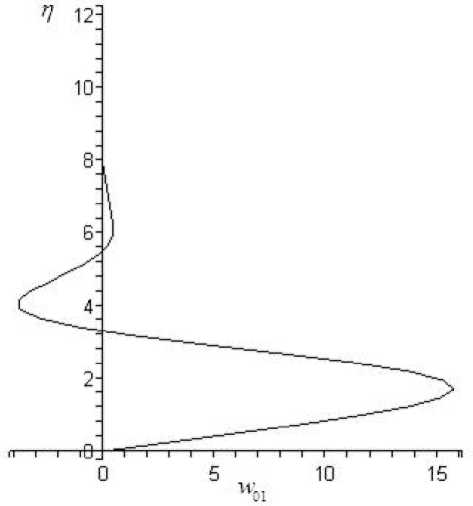
Рис. 17

dv2 + („01 + s^) 2. — (w00 + s^) P01+ dn              4 ) p00   V        4 / p00

Граничные условия:

+ su 00

4 p 00

= 0 ,

П = 0 : u 02 = v 02 = H 02 = 0 ,

П ^ ж : u 02 ^ 0 , H 02 ^ 0 .

Из решения системы уравнений (21) определяется коэффициент P (с нижним индексом "02")=-0,8 Процедура нахождения координатно-параметрического разложения и последовательность замыкания систем уравнений представлена на рис. 18.

При z ^ zk ~ V^

p = 0 , 498 - 0 , 32 e + 0 , 28 z ² - 0 , 8 e ² + 0 , 33 z ⁴ + 2 , 1 ez 2 +

+ O ( e ³ ,e ² z ² ,ez 4 ) . (22)

На рис. 19 представлено сравнение асимптотического разложения (22) и точного решения при s = 1, y = 1 , 1, ° = 1. B — точное решение и C — разложение.

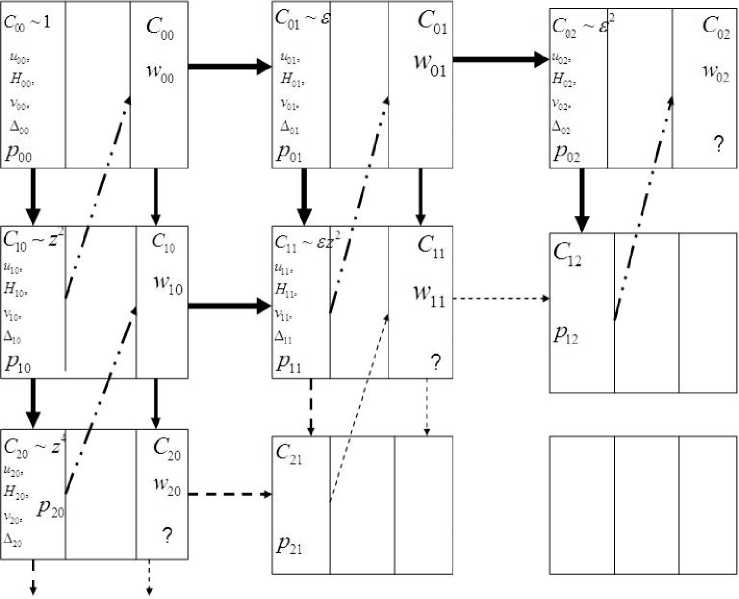
Рис. 18. Координатно-параметрическое разложение. Последовательность решения.

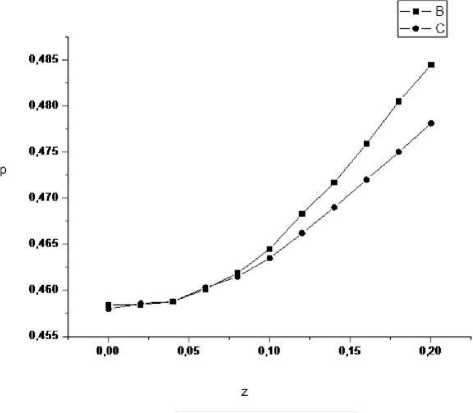
Рис. 19. Сравнение асимптотического и точного решений при s = 1, y = 1 , 1, ^а = 1. В — точное решение и С — разложение.

Выводы. В настоящей работе исследовано течение в пограничном слое на плоском треугольном крыле на режиме сильного вязкого взаимодействия с внешним сверхзвуковым потоком. Аналитическое исследование проведено в случае «ньютоновского» предельного перехода, при ко- тором показатель адиабаты стремится к единице, а значения чисел Маха и Рейнольдса — к бесконечности. Показатель адиабаты минус единица является малым параметром задачи. Сформулирована краевая задача, описывающая течение в пространственном пограничном слое на всем крыле на режиме сильного вязкого взаимодействия. Приведены результаты численных расчетов данной краевой задачи при различных значениях показателя адиабаты, близких к единице, как для закритических, так и докритических областей течения. В области докритического режима течения в окрестности плоскости симметрии крыла проведено разложение функций течения в степенные ряды по указанному выше малому параметру и по значениям поперечной координаты. Приведены системы обыкновенных дифференциальных уравнений с соответствующими краевыми условиями для определения коэффициентов членов разложения. Определены условия замыкания для некоторых из них. Проведено сравнение решения в виде разложения в ряды с численным решением системы в частных производных.

Работа выполнена при финансовой поддержке РФФИ (проект N 10-01-00173-a) и ФЦП ННПКИР (ГК № 02.740.11.0154).