О температуре в канале проплавления при электронно-лучевой сварке

Младенов Георгий Михайлович, доктор физических сварочной ванны, и в расплаве формируется глубокий и узкий канал проплавления, жидкие стенки которого удерживаются давлением паров [4-8]. Поэтому процессы испарения при ЭЛС представляют интерес при разработке теоретических моделей процесса формирования сварного шва [9-10]. На данный момент достигнуты заметные успехи в численном моделировании процессов электронно-лучевой и лазерной сварки [7-8,11-13], но законченные общепринятые модели, до настоящего времени, отсутствуют. Особенно следует указать на отсутствие динамических моделей описывающие процессы в канале проплавления при ЭЛС с периодическим воздействием на электронный пучок. Отметим также, что при моделировании сходной с электронно-лучевыми процессами лазерной сварки температуру в канале проплавления принимают обычно равной температуре кипения при атмосферном давлении, но ЭЛС ведется в вакууме, и данное допущение при моделировании процесса ЭЛС необоснованно. В предлагаемой работе описывается методика экспериментальной оценки температуры в канале проплавления при ЭЛС, которую можно применить для случая ЭЛС с осцилляцией электронного пучка.

Методика экспериментальной оценки температуры. Основой экспериментальной методики являлось определение температуры в канале проплавления при ЭЛС по данным о химическом составе паров, образующихся над зоной сварки. Для экспериментальной оценки состава паров на электронно-лучевой установке с энер-

«SELMI» (Украина) производились проходы осциллирующим электронным пучком по образцу из аустенитной стали 12Х18Н10Т. Вблизи зоны воздействия электронного пучка на образец (на расстоянии 15 мм) была установлена пластина из стекла. Мощность электронного пучка в экспериментах составляла 3,6 кВт (ускоряющее напряжение 60 кВ), скорость сварки – 3,2 мм/с, частота и амплитуда осцилляции пучка – 650 Гц и 1,8 мм, соответственно. Ионизация фокуса выбрана таким образом, что глубина проплавления была максимальна – порядка 7 мм. Схема эксперимента приведена на рис. 1. В процессе воздействия осциллирующего электронного пучка на образец из стали 12Х18Н10Т в режиме кинжального проплавления происходило испарение и последующее напыление на пластину из алюминиевого сплава элементов, содержащихся в этой стали. Далее проводился рентгенофлуоресцентный анализ полученного покрытия, и образца, по которому совершался проход электронным пучком. Полученные данные представлены в табл. 1, 2.

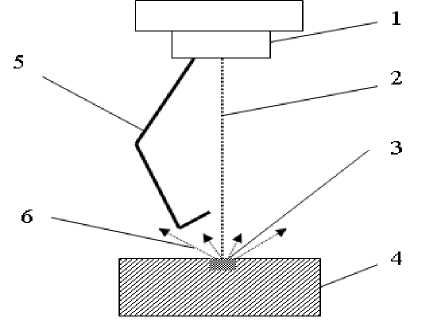
Рис. 1. Схема эксперимента по анализу испарения элементов из стали 12Х18Н10Т при воздействии электронного пучка:

• 1    – электронная пушка; 2 – электронный пучок; 3 – расплавленный металл; 4 – исследуемый материал; 5 – алюминиевая пластина; 6 – пары металла из зоны воздействия электронного пучка

Таблица 1. Химический состав исследуемого образца (сталь 12Х18Н10Т)

Химические элементы	Mn	Si	Cr	Ti	Ni	C	Fe
содержание элементов, %	1,27	0,50	18,99	0,59	10,14	0,09	68,42
стандарт, %	max 2	max 0,80	17-19	-	9-11	max 0.12	баланс

Таблица 2. Химический состав напыленного покрытия

Химические элементы	Fe	Cr	Mn	Al	Ni
содержание элементов, %	33,36	24,94	34,81	2,85	1,891

Для определения количества легирующих элементов, испарившихся из стали 12Х18Н10Т при воздействии электронного осциллирующего электронного пучка, из содержания элементов напыленного на пластину слоя вычиталось содержание элементов химического состава пластины. Результаты расчета представлены в табл. 3. Таким образом, в процессе электронно-лучевого воздействия на образец из стали 12Х18Н10Т происходит интенсивное испарение железа, хрома и марганца.

Таблица 3. Количество легирующих элементов, испаренных их стали 12Х18Н10Т

Химические элементы	Fe	Cr	Mn	Ni
содержание элементов, %	33,08	24,82	34,41	1,891

Далее, для оценки температуры в канале проплавления, образуемом в металле электронным пучком, полученные экспериментальные данные сопоставлялись с результатами термодинамического расчета. При проведении расчетов содержание каждого химического элемента в парогазовой фазе канала проплавления С i определялось с учетом химического состава металла образца (см. табл. 2) по формуле:

Ci = —

P общ

где общее давление пара Р общ в канале является суммой парциальных давлений паров элементов сплава ( Р i ) и освобожденных газов:

n

p. =Ур.

общi

Парциальное давление пара i-того элемента (Рi) определялось через парциальное давление насыщенного пара i-того элемента над чистым элементом Pi0 и активность элемента в сплаве ai по выражению где ΔНисп,i – энтальпия испарения i-того элемента; R – постоянная газовая; В – постоянная (для определенного интервала температур).

Активность элементов в сплаве a i определялась по формуле:

P i = P i 0 • a

^ai = Xi" Y i

,

Термодинамические расчеты парциального давления насыщенного пара i-того элемента над чистым элементом было осуществлен по уравнения Клапейрона-Клаузиуса [9,10]:

. 0____ _ ucni । в

• 2.3 • RT \             (4)

где Х i – атомная доля i -того элемента; γ i – коэффициент активности i -того элемента в сплаве.

Все расчеты проводились в пакете Mathcad. Результаты расчетов для парциальных давлений паров в канале проплавления по приведенным выше формулам представлены в виде графиков на рис. 2. Из графиков видно, что давление паров в канале в основном определяется давлениями трех элементов – железа, хрома и марганца.

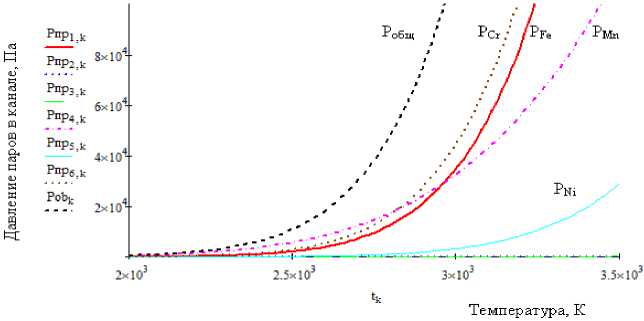
Рис. 2. Изменение давление паров в канале с ростом температуры для стали 12Х18Н10Т:

Р_Fe – давление паров железа; P_Cr – давление паров хрома; P_Mn – давление паров марганца; P_Ni – давление паров никеля; P общ – общее давление паров

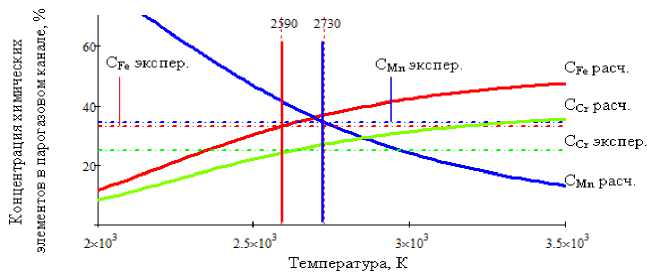
Рис. 3. Зависимость концентрация железа, марганца и хрома в канале для стали 12Х18Н10Т от температуры

Для определения температуры парогазовой фазы в канале проплавления результаты расчетов сопоставлялись с данными, полученными при экспериментальных исследованиях. На рис. 3 представлены результаты расчетов химического состава парогазовой фазы в зоне ЭЛС (представлены результаты только для железа, хрома и марганца, т.к. содержанием остальных элементов можно пренебречь) и концентрации химических элементов, полученные при рентгенофлуоресцентном анализе при экспериментальных исследованиях (горизонтальные линии). Значения температуры парогазовой фазы в канале проплавления определялись по равенству расчетных и экспериментальных значений концентрации элементов и составили: 2590 К (для Fe), 2610 К (для Cr) и 2730 К (для Mn). Как видно из полученных данных, расхождение значений температур незначительно (около 5%) и его можно объяснить неточностями используемой методики. На точность оценки температуры также влияли разброс сведения о значениях энтальпии испарения различных элементов (табл. 4), с которыми связаны результаты расчетов концентрации паров элементов.

Таблица 4. Различные значения энтальпий испарения для химических элементов, входящих в состав стали 12Х18Н10Т

Химический элемент	Значения энтальпии ∆Н, кДж/моль
	данные по [14]	данные по [15]	данные по [16]
Fe	352,0	340,2	351,0
Si	473,0	383,3	439,0
Mn	220,0	220,5	219,7
Ni	374,0	374,8	371,8
Cr	340,0	341,8	348,8

Необходимо отметить, что температура в канале проплавления непостоянна по глубине и испытывает флуктуации по времени. При осцилляции электронного пучка зона максимального энерговыделения совершает возвратно-поступательное движение от поверхности вглубь канала и обратно [17-18], в связи с чем температура какого-либо выделенного элемента поверхности канала проплавления становится периодической функцией. В соответствии с этим, описанная методика позволяет оценить лишь некоторую эффективную по времени и глубине канала проплавления температуру.

Расчет распределения температуры по глубине канала проплавления. Распределение температуры в канале проплавления при ЭЛС можно рассчитать с использованием модели, основанной на предположение о равновесия элементов стенки канала проплавления, при котором обеспечивается равенство давления паров в канале и суммарного давления гидростатических сил и сил поверхностного натяжения [2, 1213]:

P = pgh + — r                  (6)

где ρ – плотность материала; h – глубина канала проплавления; σ – коэффициент поверхностного натяжения материала; r – радиус канала.

Поверхностное натяжение и плотность материала в первую очередь зависят от температуры. С повышение температуры плотность вещества и коэффициент поверхностного натяжения снижаются. Поэтому важным является точное определение этих параметров для заданных значений температуры. Коэффициент поверхностного натяжения расплава стали 12Х18Н10Т определим по формуле, предложенной в работе [19]:

—Fe = —Fe - 2000 • lg Z (F" X . )    (7)

где σ Fe – поверхностное натяжение чистого железа, Дж/м²; Х – атомная доля -го компонента в сплаве; F – параметр, характеризующий капиллярную активность легирующих элементов. При температуре 1600⁰С значения F , для большинства элементов, входящих в состав стали 12Х18Н10Т, имеются в справочной литературе [10], а для определения F при других значениях температуры используется следующее выражение:

T        1873 T

F = ⁽ F )              (8)

Таблица 5. Значения параметра, характеризующего капиллярную активность легирующих элементов (F i ) и атомные доли компонентов (Х i ) в стали 12Х18Н10Т

Легирующий элемент	C	Si	Mn	Ni	Cr
F i	2,0	2,2	5,0	0,7	2,5
Х i	4,15∙10-3	9,88∙10-3	0,013	0,095	0,202

Из уравнений (7) и (8) получаем выражение для расчета поверхностного натяжения для стали 12Х18Н10Т для заданного значения температуры

Cт

— T

1873              1873              1873              1873              1873

= 1800 - 2000 • lg F ₂ • X ₂ + F ₃ • X 3 + F 4 • X 4 + F 5 • X 5 + F 6 • X 6

,

мДж м ²

На рис. 4 представлен график зависимости коэффициента поверхностного натяжения расплава стали 12Х18Н10Т от температуры, полученный с использованием выражения (9).

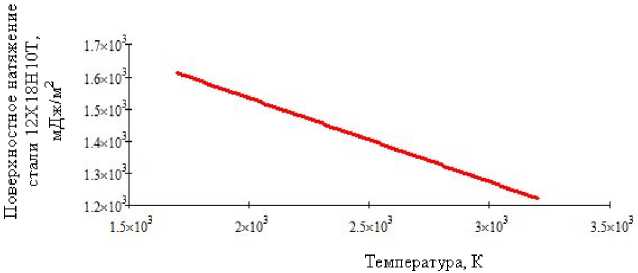
Рис. 4. График зависимости поверхностного натяжения стали 12Х18Н10Т от изменения температуры

Канал проплавления при ЭЛС имеет достаточно сложную, меняющуюся со временем форму. Аппроксимируем форму канала усеченным конусом с полусферическим дном (рис. 5) и выполним расчеты для глубины проплавления h=7 мм. Величину максимального радиуса канала (в верхней его части) в первом приближении примем равным радиусу пучка электронов R=rп=0,3 мм. Анализ корневых дефектов – пиков проплавления, формирующихся при ЭЛС остро-сфокусированным электронным пучком, показывает, что в корневой части канала его радиус на порядок меньше указанной величины. Примем радиус кривизны канала в корневой части 0,03 мм. Значения плотности стали 12Х18Н10Т в зависимости от температуры представлены в табл. 6. Результаты расчетов зависимости давления пара в канале проплавления от температуры, полученные с использованием уравнения (6) и данных табл. 6, представлены на рис. 6.

Таблица 6. Значение плотности стали 12Х18Н10Т с ростом температуры

Температура, К	2000	2100	2200	2300	2400	2500	2600
плотность ρ, кг/м3	7020	6970	6930	6880	6840	6790	6750

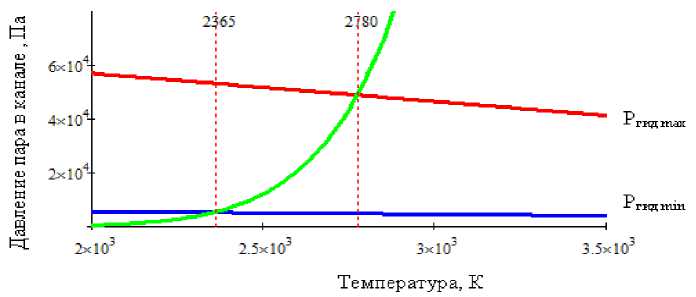
Рис. 6. График зависимости давления паров от роста температуры:

P_общ – общее давление пара в канале; P_гид – суммарное давление гидростатических сил и сил поверхностного натяжения на поверхности жидкой ванны: Р гид max – на поверхности канала, Р гид min – на дне канала

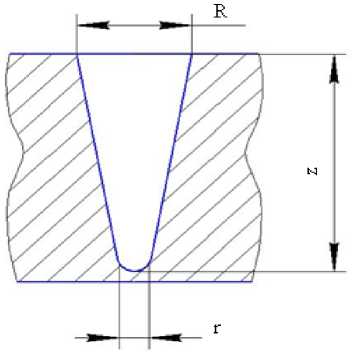
Рис. 5. Схематичное изображение парогазового канала в жидком металле при ЭЛС

Равенство давления паров в канале и давления в жидкой фазе определяет температуру на заданной глубине в канале проплавления. Для стали 12Х18Н10Т при заданных условиях интегральная температура на поверхности канала равна 2365 К, а на дне равна 2780 К. Аналогично, можно рассчитать температуру стенок канала и давление паров на произвольной глубине, для чего в формулу (6) вместо глубины парогазового канала h подставляется глубина z, измеряемая относительно поверхности свариваемого изделия (рис. 7, 8) и соответствующий этой глубине радиус кривизны канала проплавления.

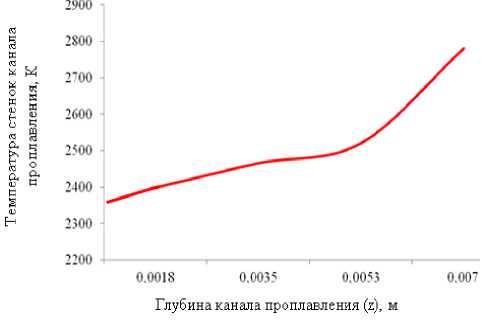
Рис. 7. Зависимость температуры от глубины канала проплавления при ЭЛС стали 12Х18Н10Т с учетом изменения глубины и радиуса канала

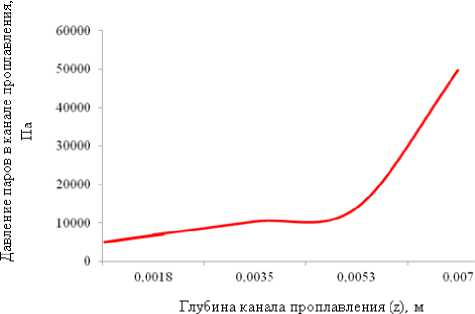
Рис. 8. График зависимости давления паров в канале при ЭЛС стали 12Х18Н10Т с учетом изменения радиуса канала

Результаты показывают, что температура в канале проплавления существенно зависит от глубины и составляет на дне канала проплавления 2800 К, а на поверхности – 2400 К. Полученные данные удовлетворительно согласуются с результатами работы [12] и с результатами, полученными с использования экспериментальной методики, описанной выше. Средняя температура стенок канала, рассчитанная по методике, основанной на оценке равновесия элемента стенки канала проплавления, имеет величину около 2600 К, а температура, определенная экспериментально по анализу испарения компонентов стали 12Х18Н10Т, составила 2660 К.

Выводы:

• 1.    Предложен метод экспериментальной оценки температуры в области взаимодействия электронного пучка со стенками канала проплавления при ЭЛС. Метод основан на измерении концентрации паров над зоной сварки с использованием химического анализа пленки, напыленной на установленную вблизи зоны сварки подложку.

• 2.    Проведено сравнение полученных путем экспериментальной оценки значений температур в канале проплавления с данными, полученными в результате расчетов с применением модели, основанной на рассмотрении равновесия элемента стенки канала проплавления, при котором обеспечивается равенство давления паров в канале и суммарного давления гидростатических сил и сил поверхностного натяжения. Определенные экспериментально значения температуры в канале хорошо согласовываются с расчетными значениями температуры стенки канала проплавления.

• 3.    При ЭЛС стали 12Х18Н10Т при глубине парогазового канала 7 мм температура на дне канала составляет величину порядка 2800 К, а давление 50000 Па. С уменьшением глубины в канале проплавления температура стенок и давление парогазовой фазы в канале уменьшаются.

• 4.    Полученные результаты в дальнейшем могут быть использованы для расчета интенсивности процессов испарения в канале проплавления при ЭЛС, что позволит определить соответствующие расходы тепловой энергии и учесть этот фактор при численном решении связанной тепловой и гидродинамический задачи.

Работа выполнена при поддержке грантов РФФИ-Урал №11-08-96016, РФФИ №13-08-00397A и при финансовой поддержке Министерства образования Пермского края.