О температурной зависимости энергии активации процесса стеклования

Машанов А. А., Мантатов В. В., Сандитов Д. С. О температурной зависимости энергии активации процесса стеклования// Вестник Бурятского государственного университета. Химия. Физика. 2019. Вып 4. С. 47–54.

Природа перехода аморфного вещества из жидкого (высокоэластического) в стеклообразное состояние остается одной из нерешенных проблем. Стеклование жидкости тесно связано с повышением вязкости при охлаждении расплава. При этом энергия активации процесса стеклования, как правило, совпадает с энергией активации вязкого течения (времени релаксации) в области перехода жидкость-стекло.

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА.

Температурная зависимость вязкости простых маловязких жидкостей типа ацетона успешно описывается уравнением Я.И. Френкеля [1]

f и n - no expl —

V RT c постоянной энергией активации U = const. Здесь η0 — предэкспоненциаль-ный множитель, R — газовая постоянная. Однако для стеклообразующих расплавов в формуле (1) энергия активации в области стеклования довольно сильно зависит от температуры: U = U(T). В связи с этим предложены эмпирические уравнения вязкости, которые в неявном виде учитывают эту зависимость U(T). Среди них широкое распространение получило соотношение ВЛФ (Вильямса-Ландела-Ферри) [2, 3]

In a_T — — C 1

T - T g

T — T g + c 2 ,

_n _ ^{t ( t} ) ~ n ^{( T} ) ^a T ^— TT g ) - ПЙ ’

где С 1 и С 2 — эмпирические постоянные, T g — температура стеклования, τ — время релаксации. Оправданность этого уравнения показана во многих работах для различных стеклующихся систем [2-4].

Ранее был предложен вывод этого выражения без конкретизации функций τ ( Т ) и η ( Т ) [5]

In a_T =

( A ² )

—

( B

T - Tg

A

^{J T} — T g +b^Tg V B

,

d ln n

= - d(T / Tg )

,

t — T g

^_ 1 d ² In n

” 2 9 ( T / T g ) 2

,

^T — T g

Было использовано разложение в ряд функции ln η ( Т ) вблизи T g по малому безразмерному параметру X = ( T — Tg^Tg [5].

Таким образом, постоянные уравнения ВЛФ (2) приобретают физический смысл, выражаясь через производные А и B

C ^-    .                                  (6)

C _— AT

• ² B^{T g} .

Настоящая работа посвящена оценке температурной зависимости энергии активации процесса стеклования U ( T ) с привлечением данных о параметрах уравнения ВЛФ С 1 и С 2 .

Расчет температурной зависимости энергии активации стеклования с помощью уравнения Вильямса-Ландела-Ферри

Легко убедиться в том, что уравнение ВЛФ (2) алгебраически выводится из известного соотношения Фогеля-Фульчера-Таммана [4]

(

П = П о exp

V

T - To )

,

где эмпирическая постоянная В o имеет размерность температуры и измеряется в кельвинах. При этом их параметры оказываются связанными равенствами

B o = C 1 C 2 , T o = T g - C 2 .

Из сравнения формул для вязкости (1) и (8), полагая в них предэкспоненци-альные множители равными, получаем следующую зависимость энергии активации вязкого течения от температуры

и = B o RT-

.

T - T o

Поскольку для многих аморфных полимеров и неорганических стекол известны значения параметров уравнения ВЛФ С 1 и С 2 [2-4], с помощью выражений (9) и (10) целесообразно перейти от зависимости (11) к величине U ( T ) как функции этих параметров

C 1 C 2 RT

T - T g + C 2

.

Из данного равенства вытекает простое соотношение для расчета энергии активации процесса стеклования U g = U ( T g ) при температуре стеклования T = T g

U g = C i RT g .

Для листового (оконного) силикатного стекла, например, С 1 и T g равны, соответственно [6]: С 1 = 36 и T g = 807 К, откуда имеем (R = 8.3 Дж/(моль.К)): U g = 241 кДж/моль. Методы релаксационной спектрометрии [4, 6] для этого стекла приводят практически к такому же значению U g = 242 кДж/моль. Для полиизобутилена ( T g = 202 К, С 1 = 38) и натурального каучука ( T g = 300 К, С 1 = 38) значения U g , равные, соответственно, 64 кДж/моль и 95 кДж/моль, также согласуются с данными, полученными методами релаксационной спектрометрии [6].

Известно, что многие стеклующиеся системы переходят из жидкого в твердое стеклообразное состояние практически при одной и той же вязкости η g ≈ const ≈ 10¹² Па·с (приближенное правило постоянства вязкости при T g ). Высокотемпературный предел вязкости η 0 ≈ η(T → ∞) также оказывается в первом приближении постоянным η 0 ≈ const ≈ 10^-3,5 Па·с. Поэтому энергию активации при температуре стеклования U g = U ( T g ) можно оценить по формуле (1) при T = T g , η g ≈ η ( T g ) ≈ 10¹² Па·с и η 0 ≈ 10 ^-3,5 Па·с [4]

U g

( n ^

= In- g RT

V  По)

g

36 RT g ,

что практически совпадает с соотношением (13).

Следовательно, слабая зависимость параметра уравнения ВЛФ С1 от природы стекол: С1 ≈ const ≈ 35–40 (табл. 1) [2, 4] объясняется приближенным постоян- ством вязкостей ηg и η0:

C 1

= In f ⁿ

V П о )

Таким образом, для расчета U ( T ) в области стеклования по формуле (12) необходимо знать значения трех величин: C 1 , C 2 и T g . Данные о параметрах уравнения ВЛФ C 1 и C 2 , а также о температуре стеклования T g , для многих аморфных органических полимеров имеются в книге Ферри [2], а для неорганических стекол — в монографии Сандитова и Бартенева [4]. Один из способов определения C 1 и C 2 описан в этой книге [4, c. 86].

Таблица

Параметры уравнения ВЛФ (2) и энергия активации процесса стеклования при T = T g для аморфных органических полимеров и неорганических стекол (использованы данные [2, 4])

№	Аморфные вещества	T g , К	C 1	C 2 , К	U g
					кДж/моль
1.	PbO — SiO 2
	PbO, мол. % 42.07	711	36	250	212
2.	Na 2 O — B 2 O 3
	Na 2 O, мол. % 2.8	544	29	130	131
3.	Листовое стекло	807	36	305	241
4.	Полиизобутилен	202	38	104	64
5.	Поливинилацетат	305	38	104	96
6.	Полиуретан	238	36	33	71
7.	Натуральный каучук	300	38	54	95

U g — расчет по формуле (13).

На рис. 1 приводится температурная зависимость энергии активации процесса стеклования для листового силикатного стекла. Кривая — расчет по формуле (12), а точки — экспериментальные данные. Экспериментальные точки получены из данных о вязкости lg η ( T ) с помощью уравнения (1), из которого следует

U = 2.3 RT [lgn(T) - lgno ]

Как видно, точки ложатся на расчетную кривую, что фактически подтверждает хорошую применимость формулы ВЛФ. Аналогичные графики U — T построены нами для ряда органических аморфных полимеров (см., например, для поливинилацетата рис. 2).

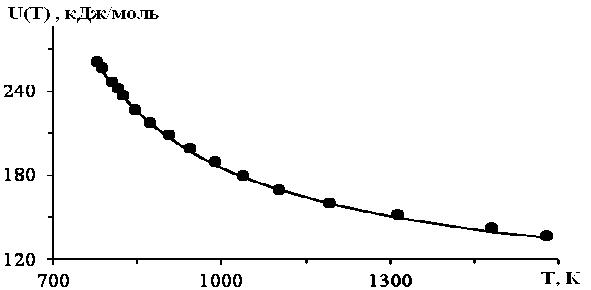
Рис. 1. Температурная зависимость энергии активации стеклования U(Т-T g ) для листового силикатного стекла. Точки — экспериментальные данные, кривая — расчет по формуле (12).

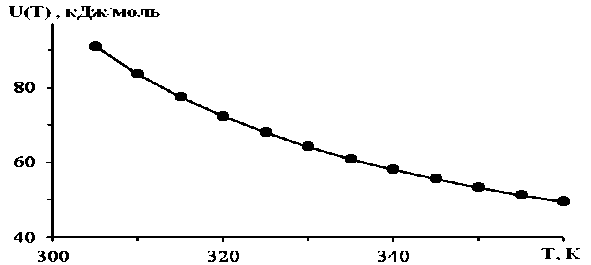
Рис. 2. Температурная зависимость энергии активации стеклования U(Т-T g ) для поливинилацетата. Точки — экспериментальные данные, кривая — расчет по уравнению (12).

В табл. 1 для некоторых стекол и полимеров приводятся значения параметров ( C 1 , C 2 и T g ), входящих в соотношение (12), а также величина U g , рассчитанная по формуле (13).

О природе зависимости U ( 7 )

Основные закономерности процесса стеклования в качественном отношении оказываются одинаковыми для подавляющего большинства аморфных веществ независимо от их природы: для неорганических стекол, аморфных органических полимеров, металлических аморфных сплавов, водных растворов, халькогенидов, что подтверждается наличием в области стеклования универсальных уравнений и правил [4-7].

Исходим из представления о том, что физической причиной резкого повышения энергии активации процесса стеклования с понижением температуры является конфигурационное изменение структуры стеклообразующего расплава.

В рамках модели делокализованных атомов [8, 9] у стеклообразующих жидкостей энергия активации процесса стеклования (вязкого течения) в уравнении (1) представляет собой сумму двух слагаемых

U = U. + Us (T) ,

где U » — потенциал перехода кинетической единицы (атома, молекулы) в новое локальное положение, U s ( T) — потенциал конфигурационного изменения структуры, который является функцией температуры,

U s ( T ) = RT ex.

^AS e

RT

Здесь A E e — энергия делокализации атома (его предельного смещения из локального равновесного положения). Делокализация атома обусловлена перегруппировкой соседних частиц (флуктуацией ближнего порядка) и отражает локальное конфигурационное изменение структуры.

При повышенных температурах RT >> A E e потенциал конфигурационного структурного изменения равен нулю U s ( T ) = 0 и уравнение вязкости (1) с учетом (21) и (22) переходит в обычную аррениусовскую (френкелевскую) зависимость с постоянной энергией активации U = U »

U- ) п = ПоехР|      I •

С этой точки зрения величина U _в оказывается высокотемпературным пределом энергии активации вязкого течения.

При низких температурах, в области стеклования, энергия делокализации атома A E e становится сравнимой с энергией тепловых колебаний решетки (~ 3 RT) и относительное число делокализованных атомов ( N e /N) , ответственных за текучесть выше T g , существенно уменьшается по закону exp( -A s / kT ) [9]. Структура расплава уплотняется и для активационного перескока атома в новое положение требуется предварительное локальное конфигурационное изменение («разрыхление») структуры вблизи него: потенциал конфигурационного структурного изменения U s ( T) резко возрастает. Этим объясняется практически экспоненциальный рост энергии активации текучести в области стеклования.

Идея разделения энергии активации текучести на две составляющие была высказана Я. И. Френкелем [1]. Дальнейшее развитие она получила в работах Филиповича [10] и Немилова [11]. При более строгом подходе под U ( T) следует понимать свободную энергию активации, как это принято в классических работах Эйринга [12].

Таким образом, конфигурационное изменение структуры, которое описывается в рамках модели делокализованных атомов, оказывается ответственным за температурную зависимость энергии активации процесса стеклования (вязкого течения) в области перехода из жидкого (высокоэластического) состояния в стеклообразное.

Заключение

Для аморфных органических полимеров и неорганических стекол рассмотрены способы расчета температурной зависимости энергии активации процесса стеклования U ( T ). Данная зависимость U ( T ) удовлетворительно описывается вблизи T g с привлечением известного уравнения Вильямса-Ландела-Ферри для вязкости (времени релаксации). В рамках модели делокализованных атомов резкий рост энергии активации в области стеклования объясняется возрастанием потенциала конфигурационного изменения структуры при охлаждении стеклообразующего расплава.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (грант № 3.5406.2017/8.9).