О теоретическом обосновании эффекта Ранка

Вместо введения приведем несколько очень кратких цитат из введения к статье Гуцола [1], которые ёмко характеризуют состояние дел с научным обоснованием этого эффекта.

Известен эффект Ранка, заключающийся в том, что в вихревых трубках достаточно простой геометрии происходит разделение потока газа на два, один из которых – периферийный – имеет температуру выше температуры исходного газа, а второй – центральный – соответственно ниже. Этот эффект выглядит еще более странным, если учестть, что … архимедовы силы должны были бы привести к "всплытию" в центре вихря более горячего газа. Эффект температурного разделения газов был обнаружен Ранком в 19321 г…. Интенсивное экспериментальное и теоретическое исследование этого эффекта … не прекращается и по сей день. Техническая простота эффекта стимулировала активность изобретателей…. Спектр разработанных и применяющихся устройств … чрезвычайно широк, а их возможности впечатляющи…. Что же касается попыток найти неоспоримое

Доклады независимых авторов 2016 выпуск 36 научное объяснение самому эффекту, то публикации на эту тему продолжаются до сих пор. Так, за последние 15 лет … (далее Гуцол указывает 21 публикацию – статьи, диссертации, книги ). … Видимо, все еще не найдено такое объяснение эффекта Ранка, которое было бы признано бесспорным. Эффект Ранка является "неожиданным явлением", природа которого "до сих пор представляется загадочной", по мнению ведущих специалистов по аэродинамике вихревых течений.

Далее Гуцол [1] рассматривает существующие теории, показывает их "внутренние недостатки и противоречия в описании экспериментальных данных", а далее предлагает собственную теорию. Однако другой анонимный автор в [2] отмечает недостатки и этой теории, а также нескольких других.

Автор данной статьи, будучи дилетантом в рассматриваемой области, не берется обсуждать приведенные выше высказывания и приводит их только для того, чтобы подтвердить необходимость поиска нового теоретического обоснования эффекта Ранка. И предложить (как водится) свою теорию, объясняющую эффект Ранка с привлечением совершенно иной области физики.

Тот же анонимный автор в [3] формулирует очень глубокое наблюдение:

Традиционная гидродинамика неявно исходит из того постулата, что естественной формой движения жидкостей и газов является ламинарное течение, а турбулентность рассматривается как его нарушение, вызванное тем или иным ограничением его «свободы». Однако, исходя из того факта, что течение, бывшее ламинарным в относительно узком канале, при удалении ограничивающих его стенок и сохранении прежней скорости начинает завихряться, логично заключить, что именно вихревое течение является «естественной» формой движения жидкостей и газов , а ламинарным оно становится вынужденно — как раз под воздействием внешних ограничений! Достаточно взглянуть на формулу числа Рейнольдса — общепризнанного критерия ламинарности или турбулентности потока, — при неизменной скорости потока оно растёт пропорционально диаметру трубы, а значит, течение становится более турбулентным. В узкой трубке мчащаяся с большой скоростью жидкость ламинарна, а в безбрежном океане даже медленные течения сопровождаются водоворотами и завихрениями — такими же медленными, малозаметными и безопасными, как и породивишие их потоки.

Это утверждение о " первичности турбулентного движения " тоже будет обосновано в предлагаемой теории.

2.    Гравитомагнетизм

В [4] анализируются некоторые масштабные природные явления и неожиданные эксперименты. Доказывается, что они могут быть объяснены существованием гравитомагнетизма и значительных по величине сил гравитомагнитного взаимодействия -гравитомагнитных сил. Эти силы имеют значительную величину в вакууме.

В слабом гравитационном поле Земли можно пользоваться максвеллоподобными уравнениями для описания гравитомагнитных взаимодействий – максвеллоподобными уравнениями гравитомагнетизма (МПГ-уравнения). Взаимодействие между движущимися массами описывается гравитомагнитными силами Лоренца (далее ГЛ-силы), аналогичными силам Лоренца в электродинамике. Из аналогии между уравнениями Максвелла для электродинамики и МПГ следует, что существует также поток S гравитационной энергии.

Как уже отмечено, ГЛ-силы имеют значительную величину в вакууме. В потоке жидкости движущиеся молекулы разъединены вакуумом. Поэтому силы их гравитомагнитного взаимодействия могут быть значительными и влиять на характер течения.

Известно, что при увеличении скорости ламинарного течения жидкости или газа самопроизвольно (без наличия внешних сил) возникает турбулентное течение [6]. Механизм самопроизвольного перехода от ламинарного течения к турбулентному не найден. Поэтому цитированное выше утверждение о " первичности турбулентного движения " представляется весьма обоснованным.

На основе вышесказанного в [5] было предложено объяснение механизма возникновения турбулентных течений. Было показано, что движущиеся молекулы текущей жидкости взаимодействуют между собой аналогично движущимся электрическим зарядам. Силы такого взаимодействия могут быть рассчитаны и включены в уравнения Навье-Стокса как массовые силы. Уравнения Навье-Стокса, дополненные такими силами, становятся уравнениями гидродинамики для турбулентного течения. При этом для расчета турбулентных течений можно использовать известные методы решения уравнений Навье-Стокса.

Далее МПГ-уравнения используются для построения математической модели трубку Ранка.

3.    МПГ-уравнения трубы Ранка

Здесь мы рассмотрим только прямоточную трубу Ранка – см. рис. 1 [1], где

• 1    – цилиндрическая труба,

• 2    – завихритель для подачи жидкости или газа по касательной к окружности трубы,

• 3    – входной поток,

• 4    – дроссель, разделяющий общий поток на центральный поток 5 и внешний поток 6,

• 7    – область трубы с завихрителем 2,

• 8    – область гладкой цилиндрической трубы (гладкая область), r , ф , z - цилиндрические координаты.

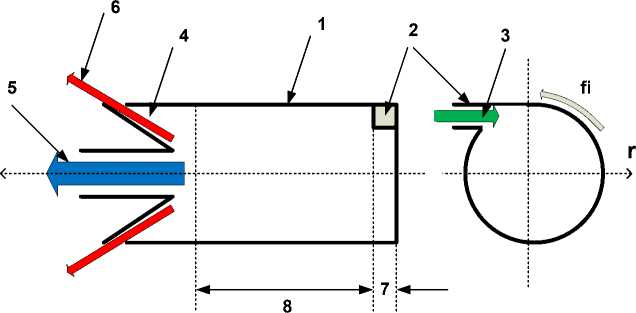
Рис. 1.

Основная задача состоит в том, чтобы объяснить, почему внутренняя энергия центрального потока 5 существенно меньше внутренней энергии внешнего потока 6.

В трубе существуют массовые токи. Обозначим их плотности как     Jr, Jф, Jz.     Эти массовые токи создают магнитогравитационные напряженности Hr, Hф, Hz. Плотности массовых токов и напряженности должны удовлетворять МПГ-уравнениям. Для стационарного случая, который имеет место в нашей задаче, эти уравнения (также, как и уравнения Максвелла для электродинамики) имеют вид div(H) = 0,                                                 (1)

rot(H) = J ,                                                 (2)

или Hr, +dk+1-H + 8H = 0,                  (3) r    8 r   r 8ф    8z 1 -'H'H- = Jr,                                      (4) r оф   оz 8Hr dHz '        = Jф,                                                   (5) оz    dr Hф ?Hф  1 5Hr +            -       = J z ■                                       (6) r    dr   r 8ф Кроме того, массовые токи должны удовлетворять условию непрерывности

div( J) = 0                                               (7)

или JJ. + «Lr + 1.5J. + aJz=o.                        (8) r   3 r   r дф   3z Можно полагать, что поле является однородным вдоль вертикальной оси oz . В приложении 1 показано, что в этом случае система уравнений (3-6, 8) может иметь следующее решение: где α1 Jr. = - - jфr cos(aФ) - ^ J^,r,                         (9) Jф. = ]фГ sin(aФ) + J^or ,                                  (10) Jz = hф ( - a 72)ЗО8(аф)+ Joz,                         (11) α Hr. = — hvr Sina),                                 (12) Jr Hф. = НфГcos(aф) + —o ,                               (13) 11 Hz = - — J»r sin(aФ) - — Jфor ■                          (14) α, jϕ, hϕ, Jϕo , Jzo - некоторые константы, определяемые конструкцией и входным потоком. 4. Область трубы с завихрителем В этой области можно определить массовый ток Jϕo как величину, пропорциональную входному потоку 3. Массовый ток Jzo можно определить как величину, пропорциональную массовому току Jϕo и постоянную вдоль длины этой области (в силу того, что эта длина мала). Наконец, при данном Jzo по (3.11) можно найти Jz . Итак, не вдаваясь в детали вычислений, можно утверждать, что на выходе этой области существует массовый ток (3.11), направленный вдоль оси oz .

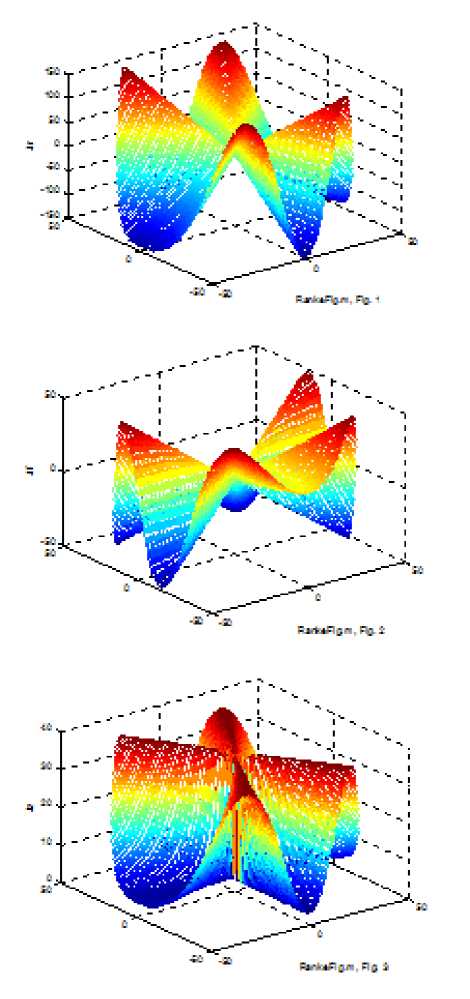
Рис. 2

5.    Гладкая область трубы

Итак, на входе гладкой области существует массовый ток (3.11), направленный вдоль оси oz , а массовый ток с плотностью J o отсутствует ( J o = 0 ). При этом по (3.9, 3.10, 3.11-3.14) могут быть найдены J_r , J _ϕ , H_r , H _ϕ , H_z , поскольку из (3.11) известны J z = a, h _p , J_oz . Полагая, что константа j _; также известна, рассмотрим полученное решение. На рис. 2 показаны графики функций - J r. , J _ф , J_z соответственно при a = 6 , j ^ = 1, h _; = 1 , Jt» = 0, J_zo = 20 .

6.    Потоки энергии

Плотность потока гравитомагнитной энергии – гравитомагнитный вектор Пойнтинга

• 5 = E x H,(1)

где гравитационная напряженность E связана с плотностью массового тока также, как электрическая напряженность связана с плотностью электрического тока, т.е.

E = p- J ,(2)

где ρ - сопротивление массовому току, вызванное вязкостью жидкости. Совмещая (1, 2), получаем:

S = pJ x H.(3)

Векторное произведение (3) в цилиндрических координатах имеет вид:

5 ' = 5 = J x H = ρ

s r s ; s z

J ₉ H_Z — JH JH - J_rH_z JH - J h

При известных J, H можно найти S'. На рис. 3 показаны графики функций (4) при a = 2. На рис. 4-6 показаны графики функций 5Г, S’’, S’ ] соответственно при a = 6, j; = 1, h; = 1,

J;, = 0, Jzo = 20 .

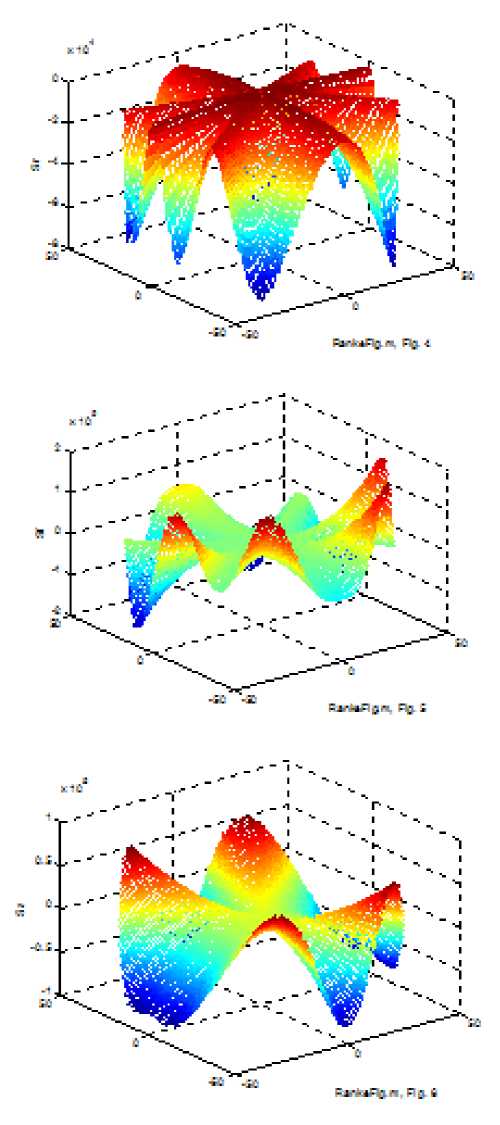
Рис. 3.

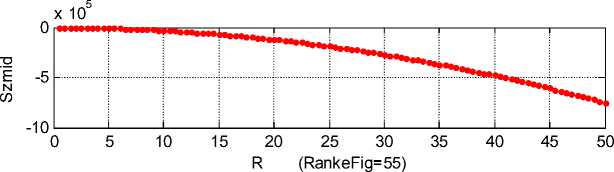
Среднюю по каждой окружности плотность потока энергии обозначим как S mid , S m , S ’ mid J . На рис. 4 показаны графики функций [ S ;mid , S^ , S mid ^J в зависимости от радиуса при ^а = 6 ,

Jv = 1, \ = 1, J

*_____________________________________________________I_____________________________________________________I______________________________________________________I_____________________________________________________I______________________________________________________I_____________________________________________________I_____________________________________________________I______________________________________________________I_____________________________________________________I______________________________________________________

0     5     10    15    20    25    30    35    40    45    50

-2

Рис. 4.

Из этих графиков следует, что потоки энергии в центральной области (при малых радиусах) близки к нулю. Потоки энергии Srmid и Sfmid расходуются на тепловые потери в сопротивлении ρ , т.е. на вязкое трение. Эти потери и определяют температуру центрального и внешнего потоков. Отсюда следует, что внутренняя энергия центрального потока 5 существенно меньше внутренней энергии внешнего потока 6.

Приложение. Решение МПГ-уравнений.

Рассматривается решение уравнений (3.3-3.6, 3.8). Из физических соображений ясно, что поле должно быть однородным вдоль вертикальной оси, т.е. должны отсутствовать производные по аргументу z , и, следовательно, уравнения (3.3-3.6, 3.8) должны быть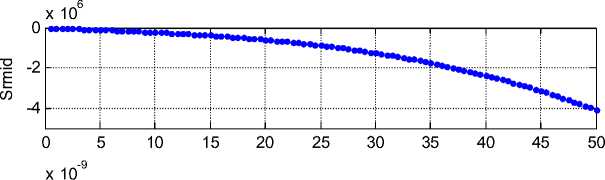

переписаны в виде: H- + ан_+LdH^—0, (1) r    8 r   r дф 1 dHz — J r , (2) r дф -dH, — J dr    ^ (3) H. + dHФ  1 8Hr +           •      — J z, (4) r    dr   r дф ± +J+1.J — 0 (5) r   dr r дф Предположим, что Hr. — hrr sin( аф) (6) Hф.— hфr со8(аф)+ Hфor (7) Из (1, 6, 7) следует: hj 81п(аф),. ./ x ,    • / \ n —----+ hr 81п(аф)- h а 81п(аф)— 0, rϕ (8) Следовательно, hr— ha 12 • (9) Из (4, 6, 7) следует: hr со8(аф)        z x                z x —+ h со8(аф)+ 2H - hra со8(аф)— Jz. rϕ             ϕ (10) Из (9, 10) следует: Jz — hф(1 - a72)^о8(аф)+ Jzo , (11) Jzo — 2 H(po. (11а) Предположим, далее, что Jr . — jrr со8(аф) + Jror , (12) Jф• — jфr 81п(аф) + Jфor . (13) Из (5, 11, 12) следует: jr cos(a^)+ j cos(a^)+ 2Jo + j^a cos(ap)+ J^ = 0, (14) r

Следовательно, jr =- jval 2.(15)

Jo =— J

Предположим, что, что

Hz = - 2 P sin(aP) - 2 J^r .(16)

Из (12, 15, 15а) следует, что выполняются условия (2, 3), которые

принимают соответственно вид:
dH  a P = - у Vcos(aP),		(17) (18)
	dH z = зфг sin(a^) Jr, dr
Итак,
	Jr.=- ta j> cosa) - 2 J»or	(12)
	JV. = j^r sln(aT)+ J^or ,	(13)
	Jz = hp( - a72)^os(a^)+Joz ,	(11)
	Hr . = -2 hpr sln(aP) ,	(6)
	Jr Hp.=hprcos(ap)+2o ,	(7)
	Hz =-2 jpr 2sln(aP) - 1 Jpor 2.	(16)