О тестировании конечно-разностной схемы для моделирования процесса вязкой диффузии с учетом сжимаемости газа в двумерном случае

При расчете течений воздуха с относительно большими дозвуковыми скоростями возникает подзадача расчета вязкости потока с учетом сжимаемости. Соответствующие уравнения данной подзадачи приводятся, например, в [1, 2]. Правильный выбор шага интегрирования по времени является важным при расчете таких течений. В предыдущих работах [3, 4] автором было найдено правило для выбора шага по времени в подзадаче диффузии для несжимаемого потока. Протестируем это правило для случая сжимаемого течения. Тестирование будем производить на примере двумерной задачи об импульсном старте плоской пластины (задача Стокса) [5].

5p + d(pu) + d(pv) = 0 dt    dx     dy и энергии dE d(Eu) d(Ev)

— +     +——--div(Pv) = 0 , (3)

dt dx dy где d              d div(Pv) = — (PnU + Pi2v) + — (P2iu + P22v) . (4) dx             dy

Здесь du 2

d x

, du 2 (d u d v P 11 = ^-P ⁺ 2ц-—-ц —-^т , d x 3 V d x d y ^

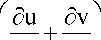
d y d x _v

P 12 = P 21 =ц

Уравнения Навье-Стокса для сжимаемого газа [1] в двумерном случае имеют вид

d v 2

du p a=

^^^^^^^s

d p   _ d (  d u ]   d    (d u   d v

+ 2 I ц1 +ц + d x d x ( d x )  d y ( (d y   d x

^^^^^^^B

2 d

3 d x

V (d x d y J J

d u

^^^^^^^s

_  d v  2 (d u   d v

P₂₂ ^=- P + 2ц---ц-- 1--

d y 3 (d x d y_v .

Также необходимо добавить уравнение состояния

E = —— +¹ p (u ² + v²] к- 1 2 ^k

dv p dT =

d u

^^^^^^^s

d p   d

1ц1

d y d x ( (d y d x

+ 2 — ц — d y    d y J

^^^^^^^s

или    p C_vT = —^ . (6)

к- 1

^^^^^^^B

При этом коэффициент динамической вязкости для воздуха для (1) и (5) определяется следующим выражением [2]

Для замыкания задачи необходимо добавить уравнение неразрывности

ц = 1,45 x 10 ^{- 6}

T32

.

T + 110

При решении данной задачи методами, использующими расщепление по физическим процессам, возникает задача о моделировании процесса диффузии. Данная задача будет опи-

сываться следующими уравнениями

d ( p u) а

„ Г дц д и     д ²и ) 5ц Г d u dv )

= 2 I —— + Ц— т I+—I —+— 1 +

(д х д х     д х² J д у ( д у д х J

Гд 2и д ²у )

Ц(д у² д х д у J

2 [ дц Г д и 5 v ) Гд ²и 5 ²v т I 1 У^ + УТ^- 1 ^{+ ц}1 уу^ + ~

3 ( д х ( д х д у J   ( д х² д у д х

5 ( p v)  дцГд и   5 v )   Г д ² и    д ² v )  „Гдцд у     5 ²v

= — I — + — | + ц|---+ —? 1 + 2I —— + ц—- ду    дх (ду  дх J   (дудх  дх2 J (ду ду   ду

Здесь h – шаг ячейки расчетной сетки по пространству h = ₄ х = ₄ у . В работе [4] путем серии численных экспериментов было найдено значение k = 0.22 , при котором ошибка решения минимальна. Применим это значение и в нашей численной схеме.

2. ТЕСТИРОВАНИЕ ЧИСЛЕННОЙ СХЕМЫ

^дц ₍д у

д и 5 v 1 д х д у

Г д ²и (д х д у

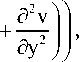
дЕ , д(ци) ди , д2и 2 д(ци) Г ди ду) 2 Г д2и д2у = 2         + 2ци^-^I    +   |--ци|     + д1      дх  дх      дх2  3  дх  (дх  ду)  3   (дх2  дхду

д ( ц v) Г д и   5 v (    Г д ²и    д ²у )  д ( ц и) Г S v   д и (    Гд ²и д ²у )

+11| + цvI+I +1+I + ци I         +I + дх (ду  дхJ    (дхду  дх2 J   ду (дх  дуJ    (ду   дхдуJ

В качестве тестовой задачи была выбрана первая задача Стокса об импульсном старте плоской стенки [5]. При обращенном движении эту задачу можно рассматривать как продольное обтекание бесконечно длинной плоской пластины равномерным потоком со скоростью u „ . В данном случае аналитическое решение данной задачи имеет вид

_{+ 2} д ( ц v) S v д у д у

_ d² v  2 5 ( u v) Г д и   d v (   2    Г д ² и    д ² v

+ 2uv    -       |   +   I— uv!     + ду   3 ду (дх  дуJ  3   (дхду  ду

u e _x = er ^f( n ⁾ , n=

y

V4 V 1

.

Для конечно-разностной аппроксимации системы уравнений (8, 9) использовались следу-

ющие схемы:

д(ри) яР‘+4tut+j4t -p‘,ju‘,j д           Д t ди ~ Ц^-иЦ^

д х      2 ₄ х ,

Расчетная область представляла собой прямоугольник размерами 2b х 0.2b , в центре которого в направлении, совпадающем с осью OX, располагалась плоская пластина длины b. Использовалась однородная расчетная сетка 200 х 20 ячеек.

Были получены профили безразмерной скорости

*

Uj =

u j

^и »

д2и ~ ut-i,j - 22ut,j + ut+i,j дх2            лх2

^д 2^и ^ u i + 1,j + 1    u i + 1,j - 1    u i - 1,j + 1 ^{+ U}i - 1,J - 1

^{5 х 5} у             ⁴ 4 ^х 4 у

где ₄ 1 - шаг по времени, а ₄ х и ₄ у - по пространству. Индекс i отвечает за изменение переменной вдоль оси x, j – вдоль оси y. Остальные производные аппроксимируются аналогичным образом.

Граничные условия прилипания потока на поверхности пластины для слоя фиктивных ячеек J = 0, находящихся с «обратной стороны» пластины, сводятся к ui,0 = —ui,1 , vi,0 = 0 , (11) где ячейка с координатами (i,0) является прилегающей к поверхности пластины.

В работах [3, 4] было показано, что при выборе шага по времени в виде

₄ 1 = kh²/ v (12) ошибка численного решения уравнения диффузии с помощью схемы «донор-акцептор» и схемы «вперед по времени, центральная по пространству» (ВВЦП) зависит только от константы k и от количества сделанных шагов по времени.

для трех сечений, располагавшихся на расстояниях: 0.25b, 0.5b, 0.75b, – от переднего края пластины в численной схеме. В силу выбора переменной п данные профили будут совпадать для разных сечений, и для трех проведенных расчетов. Эти численные расчеты были со следующими начальными условиями (см. таблицу 1). Остальные одинаковые для всех трех случаев начальные условия были равны: скорость набегающего потока и _ю = 14.63394141 м/с, температура T = 290.511 K, динамическая вязкость ц = 1.79266 х 10 ^{— 5} кг/(мхс).

При проведении расчетов для разных величин h и n выяснилось, что, как и в [3, 4], порядок ошибки численного решения зависит только от константы k и количества сделанных шагов по времени. Максимальная относительная ошибка решения определялась следующим образом

5 = тах

I I                   и. — иех(у.)

a j - 100% , a j= -и   e^J , (15)

u^* ex (y j )

где u^*_j – численное решение, u_ex (y_j ) – аналитическое решение.

Сравнение профиля скорости, полученного численно с помощью рассмотренной схемы, с аналитическим решением показано на рис. 1. При этом для выбранного значения k = 0.22 максимальная погрешность для профиля ско-

Таблица 1. Начальные условия, при которых проводились расчеты

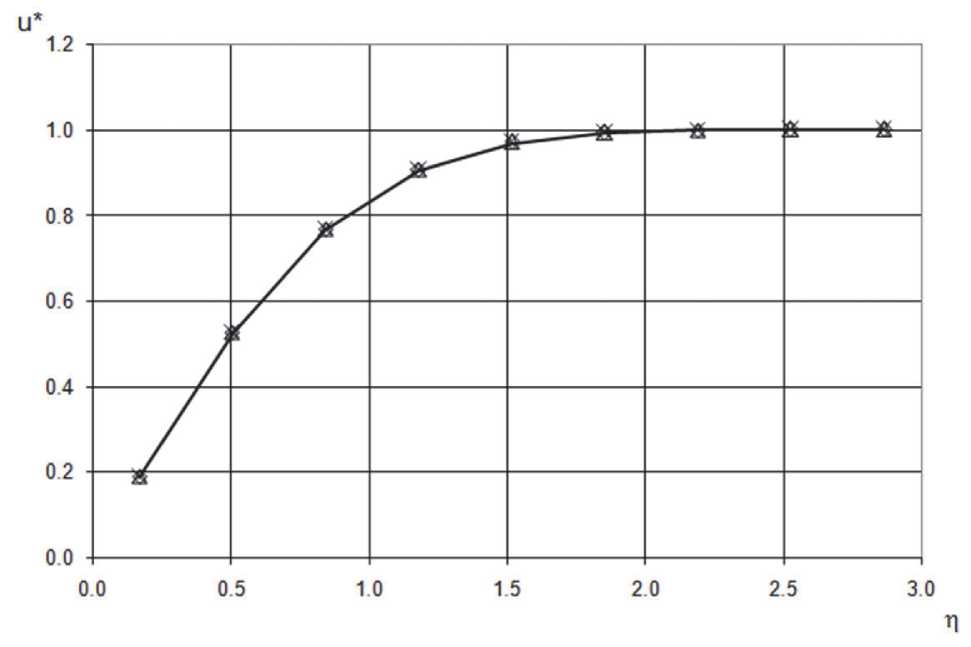
Рис. 1. Распределение продольной безразмерной компоненты скорости u* над поверхностью пластины в сравнении с аналитическим решением; численное решение: – сечение x = 0.25b , – сечение x = 0.5b , – сечение x = 0.75b , – аналитическое решение (12)

рости вдоль линии, перпендикулярной центру пластины, (0.5b) составляет 0.32% для всех трех расчетов.

Это позволяет сделать вывод, что значения коэффициента k, при котором получается достаточная точность решения задачи Стокса для схемы ВВЦП [4], и схемы, рассмотренной в данной работе, совпадают.