O точности численных методов решения уравнений Вольтерра I рода в задачах теплопереноса

В современных технологических процессах, связанных с процессами теплообмена, особое внимание уделяется выбору соответствующих температурных режимов, позволяющих реализовывать требуемые свойства объекта. Прогнозирование результатов воздействия выбранного режима внешнего теплового воздействия вызывает большой интерес у исследователей. Результаты некоторых исследований, посвященных теплопереносу и динамическим измерениям, представлены в работах [1–8].

Осуществление достоверного прогнозирования напрямую зависит от точности решения соответствующих задач измерения, возникающих в ситуациях, когда требуется оценить результаты предполагаемого внешнего теплового воздействия на изменения температуры в контрольной точке объекта. Математически в линейном приближении задача измерения, связанная с проблемой определения температуры в контрольной точке, представлена в виде обратной граничной задачи для уравнения теплопроводности с начальными и граничными условиями.

Граничные и начальные условия в задаче измерения, связанной с теплопереносом, формируются на основе результатов температурных измерений, получаемых от различных датчиков температур. Как правило, датчики расположены вблизи внешней границы объекта, и одним из актуальных направлений в решении прикладных задач прогнозирования и связанных с ней задач измерения является разработка методов, позволяющих по результатам граничных измерений определить температуру во внутренних контрольных точках объекта.

В д а н н ой ра б оте п ре дс тав ле н ы ре зу льта ты с равн ите л ьн ого а на ли за точности численных ре ше н и й з ад а чи и зме ре н и я, ос н ов анных на интегральной аппроксимации, и в ы чи с ли те льной с х е мы , ра зра б от а н н ой н а ос нов е оптимального по порядку метода регуляризации . На д е жн о с ть и э ф ф е к ти вн ость п ос тро е н н ых ме тодов п одт в е рж де н а ре зу льта та ми вычислительного эксперимента, п ров од и мого н а ос н ов е тес тов ых примеров. Предложенные методы могут пос лу жи ть ос н ов ой д ля р а з раб от к и ме тод ов обраб отк и результатов поверхностных температурных и зме ре н и й с ц е лью о с уще с тв ле н и я п рогн озир ов а н и я те мп е ра ту ры в о в н у тре нних контрольных точках.

Постановка задачи

Рассмотрим задачу измерения, связанную с определением температуры в контрольной точке объекта по результатам граничных измерений. Процесс теплопереноса осуществляется в ситуа- ции, когда внутренние тепловые источники не оказывают существенного воздействия на изменения температуры внутри объекта, а основные характеристики процесса теплопереноса – плотность материала, коэффициент теплоемкости, коэффициент теплопроводности – не претерпевают существенных изменений по пространству и времени. Известно, что в начальный момент времени температура в каждой точке объекта была одинаковой. Геометрическая схема измерения представлена на рис. 1. Датчики измерения температуры расположены в точках O и x0 , и по результатам измерений требуется определить температуру в контрольной точке A .

Рис. 1. Геометрическая схема измерений

Введем следующие обозначения. Пусть x – расстояние от точки O , расположенной на границе объекта, до текущей точки на прямой OA, x е [0,£], температура в точке x в текущий момент времени ха- рактеризуется функцией u (x, t).

С огл а с н о п од х од у , изл ожен ному в работе [9], в линейном приближении мате ма ти че с ка я м о де ль те плоп е р е н ос а п р е д ста в ле н а у ра в н е н и е м те п л оп ров од н ос ти :

рые приближения g _δ ( t ) и уровень погрешности δ >0 такие, что g _δ ( t ) - g ₀ ( t ) _C ≤ δ . Требуется найти значения функции φ_δ ( t ) , получаемой в результате внешнего воздействия g _δ ( t ) , удовлетворяющей (1)–(4) и оценить уклонение φ_δ ( t ) от φ ₀ ( t ) .

Получаемая задача измерения относится к классу обратных задач и для ее решения необходимо использовать регуляризующие подходы [10–14].

Интегральная модель теплопереноса

В работе [15] исходная задача (1)–(4) сводится к интегральной модели с помощью прямого и обратного преобразований Лапласа, при этом регуляризующий подход используется после применения обратного преобразования. Использование преобразований Лапласа допустимо в силу свойств функций u ( x , t ) , g ( t ), φ ( t ) , а регуляризирующий подход позволяет установить прямую зависимость неизвестной функции φ ( t ) от контролируемого внешнего теплового воздействия g ( t ) . Результирующее уравнение в интегральной модели имеет следующий вид:

t

A φ = ∫ K_N ( t - s ) φ ( s ) ds = y ( t ), 0 ≤ s ≤ t ≤ T , 0

π ² q ² a ( t - s )

Л                 Z2/3

KN (t - s) =E(-1)q1 q2e    e , y(t)=тт g(t), q=1                                  2π где параметром регуляризации является количество слагаемых N в ядре KN (t,s) . Из этого уравнения требуется найти функцию φ(t) при условии, что yδ(t) - y0 (t)

< 8l ³

^C ≤ 2 π ² .

Решению урав-

нений Вольтерра посвящены работы многих исследователей (см., например, [16, 17]). Преимущество использования представленной интегральной модели заключается в том, что из вычислительной схемы исключается неустойчивая численная процедура обратного преобразования Лапласа, а для приближенного решения интегрального уравнения (5), (6) применяются численные методы, обладающие свойством саморегуляризации. При этом в качестве «естественного» параметра регуляризации выступает шаг дискретизации, определенным образом согласованный с уровнем погрешности исходных данных δ .

Специфика уравнений Вольтерра

Основная особенность уравнений Вольтерра, получаемых в результате построения интегральной модели, заключается в том, что ряд (6), определяющий ядро, является знакопеременным, что требует разработки специального подхода к выбору величины N , гарантирующего корректрость решения задачи (5), (6).

Заметим, что при решении (5), (6) возникают несколько видов погрешностей, связанных с погрешностью численного метода, а также с аппроксимацией исходной задачи (1)–(4). Остановимся сначала на втором виде погрешностей, обусловленных выбором величины N в ядре K_N ( t , s ) , заданном формулой (6). Без ограничения общности в дальнейшем полагаем, что I = 1, a = 1.

В статье [18] показано, что на точность значений K_N ( λ ) , где λ = t - s , в (6) с ростом параметра N влияет специфика операций машинной арифметики. Известно, вещественное число x = s ⋅ M ⋅ 10 ^{- L + p} можно однозначно определить значениями ( s , M , p , f ) , где s ∈ { - 1, 0, + 1} является знаком числа, M ∈ {10 ^{L - 1},10 ^{L - 1} + 1,...,10 ^L - 1} ∪ {0} – мантисса числа, L – число позиций мантиссы, p – порядок числа. Дополнив общепринятое представление вещественного числа параметром f , который соответствует числу достоверных цифр в мантиссе (начиная слева), проиллюстрируем изменение точности результата.

Приведем типовые случаи накопления систематических ошибок. Расчеты выполним в системе компьютерной алгебры MAPLE.

Пример 1. Пусть в ядре (7) количество слагаемых N = 50 . Полагаем

34                 2 2            502 2

x1= ∑(-1)q+1q2e-π2q2λ0, x2= ∑(-1)q+1q2e-π2q2λ0, q=11

10                 2 2             502 2

x3=∑(-1)q+1q2e-π2q2λ0, x1= ∑(-1)q+1q2e-π2q2λ0. q=1

Вычислим значение KN(λ0) , λ0 = 10-3 при длине мантиссы L ≥ 8 . В таблице даны резуль таты точности вычисления суммы xΣ = x1 + x2 и разности x∆ =| x4 | - | x3 | .

Зависимость точности вычисления от параметра N

L	M Σ	f Σ	M ∆	f ∆
8	18656737	6	00000006	0
9	186567422	8	000000004	0
10	1865674269	8	0000000006	0
11	18656742737	11	00000000014	1
12	186567427373	11	000000000133	3
13	1865674273715	12	0000000001339	4
14	18656742737137	13	00000000013396	4

Мантиссы суммы M _Σ и разности M _∆ приведены во втором и четвертом столбцах таблицы, количество достоверных цифр f _Σ , f _∆ в мантиссах указано в третьем и пятом столбцах соответственно.

Таким образом, для обеспечения гарантированной точности вычислений значений функции K_N при t → 0 с ростом числа слагаемых N в (6) требуется увеличивать длину мантиссы L .

Численные методы

Перейдем к численным методам решения уравнения (5), (6). Введем равномерную сетку уз-1T лов ti = ih, tj-1 = ( j - 2)h, i = 1,n, j = 1,i, n = . Определим значение шага дискретизации в зави-

• ⁱ          j - 2          2                               h

симости от параметра N .

Вычислительный эксперимент в [18] показал, что с увеличением числа слагаемых N в (7) значения корней λ* уравнения KN (λ) = 0 убывают (при этом имеет место монотонность отдельно по четным и по нечетным N ). Величина λ* ограничивает сверху величину шага дискретизации h , гарантируя тем самым отличие от нуля значение сеточного аналога функции KN в пер- вом узле сетки. Напомним, что условие KN (0) ≠ 0 является необходимым условием для корректности (5), (6) на паре пространств (C, C[(01,)T]), где y(0) = 0 , y′(t) ∈ C[0,T] , t ∈ [0,T] .

Аппроксимация интеграла в (5) реализовывалась с помощью product integration method и квадратуры средних прямоугольников. Сеточный аналог, получаемый с помощью product integration method, имеет следующий вид:

N               i           ^jh

∑ ( - 1) ^{q + 1} q ² ∑ φ ^h _{j -} 1   ∫ e ^{-π 2 q 2}( ^ih - ^s ) ds = y i ^h ,

q=1              j=1    2 (j-1)h а сеточный аналог, получаемый посредством квадратуры средних прямоугольников, определяет-

ся формулой:

Ni h ∑ ( - 1) ^{q + 1} q ² ∑ e

q =1

j =1

-π ² q ²( j - ¹₂) h h          h

φ i - j + ¹ ₂ = yⁱ

соответственно. С целью оценки точности применения методов, учитывающих специфику урав- нения, был проведен сравнительный анализ погрешностей решений, получаемых с помощью этих методов, с погрешностью приближенных решений, найденных посредством оптимального по порядку метода.

Согласно [19], оптимальным методом является метод, имеющий наименьшую погрешность численных решений. Метод является оптимальным по порядку, если погрешность численных решений, полученных этим методом, имеет тот же порядок, что и погрешности численных решений, полученных с помощью оптимального метода.

Рассматриваемый в данной работе оптимальный по порядку метод использовался для непосредственного решения задачи (1)–(4) без перехода к интегральной модели. Метод основан на применении преобразований Фурье и проекционной регуляризации. В работе [20] доказано, что использование метода проекционной регуляризации позволяет находить приближенные решения задачи (1)–(4) с гарантированной точностью, когда порядок погрешности вычисляемых значений является наименьшим из возможных.

Вычислительная схема метода представлена в работе [15]. Основные этапы вычислительной процедуры заключаются в следующем. Сначала к исходным данным g ( t ) применяют интегральное преобразование Фурье, реализуемое с помощью стандартных программных продуктов. Далее, используя проекционную регуляризацию, полученные образы g_F ( X ) преобразуют в значения g_F ( X , а ( 5 ) ) в зависимости от допустимого уровня погрешности 5 . Параметр а выбирается из принципа невязки. Затем определяют Фурье-образы u_F (X) численного решения согласно формуле

• 2    sh U|I

u F ^{( X )} =---- g F (^X , ^{а ( 5 )} ) ,                                                                   (9)

ц!- t

a где ц = —U(1 + i). Приближенные решения задачи (1)-(4) определяются формулой 2

^ф 5 ⁽ t )

Re(uF (Лt)),

.       0,

t >  0, t <  0.

Порядок теоретической погрешности метода, основанного на проекционной регуляризации, со- ставляет

II ^ф 5 ⁽ t ) ^-ф 0 ( t )H ln

1 1 5J

и, согласно критерию оптимальности, является оптимальным

по порядку.

Результаты вычислительного эксперимента

Найдем приближенные решения задачи (1)–(4) с помощью (5), (6) с заданным достоверным числом цифр в сеточном решении. Рассмотрим случай, когда правая часть (5), (6) известна точно. Также найдем приближенные решения Ф 5 ( t ) задачи (1)-(4) для приближенных значений g 5 ( t ), используя оптимальный по порядку метод (9), (10), основанный на проекционной регуляризации заданных с уровнем погрешности 5 .

Пример 2. Пусть N = 2, h = ™y, T = 1 • В качестве тестовой функции ф о ( t ) используем

। / х 1 — e ^ф( t ) = —

1 - e

t а                         1

у - 1, а = 10 ¹ . На рис. 2 приведены графики погрешностей е j = ф ( t ) -ф ₀ ( t ) , j = 1,4 ,

а

сеточных решений.

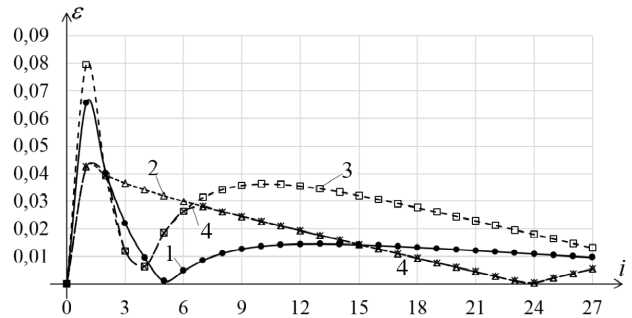
Рис. 2. Погрешности сеточных решений при точно заданных исходных данных

Результаты сравнительного анализа погрешностей методов при точно заданной правой части уравнения (6) представлены на рис. 2. По оси абсцисс указаны номера итераций. График 81 (линия 1) иллюстрирует погрешность решения, полученного с помощью оптимального по порядку метода. График 82 (линия 2) соответствует погрешности решения, полученного с помощью product integration method. График 83 (линия 3 ) соответствует погрешности решения, полученного с помощью метода средних прямоугольников, а график 84 (линия 4) иллюстрирует погрешность результатов комбинированного использования разностных методов. В результате погрешность 84 комбинированного метода составляет 84 = min{| 82 |,| 83}, а максимальные значения погрешностей составили max 8, = 0,0656,              max 82 = 0,0424,

1 < i < 27                                       1 < i < 27

max 8₃ = 0,0795,              max 8 = 0,0424.

1 < i < 27                                       1 < i < 27

Вычислительный эксперимент показал, что оба разностных метода имеют порядок сходимости O ( h ²), хотя при сравнении 8 2 и 8 3 получено, что применение метода интегрирования произведения предпочтительней, так как max 8₂ <  max 8₃.

1 < i < 27       1 < i < 27

Учитывая, что исходные данные известны с некоторой погрешностью 5 , рассмотрим случай пилообразного возмущения сеточной функции:

У(ti) = y(ti) + (-1)i 10-3, i = 1,27, nh = 1, обозначив модуль погрешности численного решения при возмущенных исходных данных через 8j, j = 1,4. Выбор шага для вычисления решения (5), (6) проведем с помощью метода Фибоначчи с десятью испытаниями. На рис. 3 приведены модули погрешностей сеточных решений с шагом h = ” (это значение с точностью 5 = 10-3 соответствует величинам, которые получены с помощью метода Фибоначчи при фиксированном уровне возмущений). При этом максимальные значения погрешностей решений для возмущенных исходных данных составили max 8, = 0,0629,              max 82 = 0,06 1 9,

1 < i < 27 ¹                                    1 < i < 27 ²

max 8₃ = 0,063 8,              max 8 = 0,0609.

1 < i < 27                                       1 < i < 27

Из рис. 3 видно, что наименьшую погрешность из аппроксимационных методов имеет решение (5), полученное с помощью комбинации метода средних прямоугольников (7) и product integration method (8). При этом, несмотря на то, что для оптимального по порядку метода с увеличением числа итераций наблюдается значительное уменьшение значений погрешности 81 , но на начальном этапе эти значения достаточно велики.

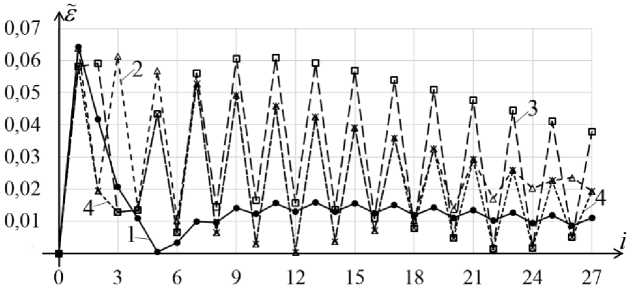
Рис. 3. Погрешности сеточных решений при возмущенных исходных данных

Таким образом, результаты экспериментов для невозмущенных и возмущенных значений y ( t ) показывают сопоставимость по точности вычислений φ ( t ) подходов, основанных на применении оптимального по порядку метода и предлагаемых численных методов приближенного решения интегрального уравнения (5), (6), основанных на интегральной аппроксимации.

Заключение

В работе представлены результаты сравнительного анализа точности численных методов уравнения Вольтерра I рода со специфическим ядром и оптимального по порядку метода решения обратной граничной задачи теплопроводности. Численные методы решения интегрального уравнения основаны на использовании product integration method и квадратуры средних прямоугольников. Оптимальный по порядку метод основан на преобразованиях Фурье и проекционной регуляризации. Показана динамика изменения погрешности каждого метода на каждом итерационном шаге. Показана сопоставимость величин погрешностей аппроксимационных численных методов и оптимального по порядку метода.

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации прикладных научных исследований в рамках базовой части Государственного задания «Разработка, исследование и реализация алгоритмов обработки данных динамических измерений пространственно-распределенных объектов», техническое задание 8.9692.2017/8.9 от 17.02.2017.