О точности определения надежности систем статистическими методами

Традиционно точность статистических оценок, в том числе и надежности, принято определять, используя известные методы расчета доверительных вероятностей на доверительных интервалах. Но эта оценка относится к номинальным значениям, полученным в результате вероятностно-статистических расчетов. При этом сама оценка принимается как безусловная данность. В предлагаемой работе рассматриваются диапазоны возможного рассеяния расчетных оценок надежности элементов и функциональных систем. Рассеяние характеристик надежности элемен- тов определяется по результатам их испытаний. А рассеяние характеристик надежности систем определяется случайным процессом их формирования из элементов .

Функциональные системы самолетов (например, гидравлическая, топливная, кондиционирования воздуха, система электроснабжения и др.) формируются путем последовательного и параллельного соединения элементов в определенные структуры. Элементами систем являются механические и гидромеханические агрегаты, электронные блоки и преобразователи. Характерной особенностью эксплуатации самолетных систем является их восстанавливаемость. После посадки самолета любой отказавший элемент заменяется исправным. При расчете надежности таких систем традиционно применяют теорему умножения вероятностей, в соответствии с которой при последовательном соединении перемножают вероятности безотказной работы, а при параллельном – вероятности отказов. Границы применимости такого подхода подробно проанализированы в работах [1–3].

В предлагаемой работе, в порядке обсуждения, исследование вопросов точности и рассеяния вероятностных оценок надежности систем, выполнено с использованием нового методологического подхода, в котором теорема умножения вероятностей не применяется [4; 5]. Предлагаемый подход основан на том, что вероятность первого отказа элемента в системе определяется суммарным параметром потоков отказов элементов, составляющих систему, и ее наработкой. В работах [3–5] предложено, при стационарном процессе эксплуатации восстанавливаемых авиационных систем, в качестве математической модели вероятности времени отказов элементов, принимать распределение равномерной плотности. Тогда вероятность отказа первого элемента в системе определится как q1(t)=ωΣ ⋅t, 0 ≤t ≤1 ,               (1)

ωΣ

где ω_Σ – суммарный параметр потока отказов N элементов, составляющих систему, определяемый как

N

ω_Σ = ∑ ω _i ,                      (2)

i = 1

где ω _i – параметр потока отказов i -го элемента в системе.

В случае когда все элементы системы имеют одинаковые параметры потоков отказов выражение (2) будет иметь вид

ωΣ =N⋅ω.

Данный подход обеспечивает возможность определения времен отказов элементов, при которых происходит изменение структуры системы. И позволяет рассчитывать надежность систем как без учета восстановления, так и с его учетом. Методы решения этих задач применительно к расчету надежности функциональных систем самолетов гражданской авиации, изложены в работах [6–8]. В предлагаемой работе оценка точности значений времени до отказа элементов выполнена только применительно к первому отказу в системе. Следует сразу отметить, что при решении задач вероятностно-статистическими методами мы не можем заранее знать, какой именно элемент откажет в момент времени t 1 .

Положив вероятность первого отказа q ₁ ( t ) = 1, определим из (1) время первого отказа в системе как t 1 = ¹ .                              (3)

ωΣ

В целях получения и сравнения числовых оценок рассмотрим расчет для приближенного аналога гидросистемы самолета Ту-154М. Гидросистема состоит из N = 60 элементов, расположенных в трех параллельных подсистемах, по 20 последовательно включенных элементов в каждой. В расчетах аналога, примем параметр потока отказов для всех элементов одинаковый и равный ω = 1 ⋅ 10 ^{- 4}ч ^{- 1}, так как гидросистема самолета Ту-154М имеет примерно такие же значения для агрегатов. Время до первого отказа в системе не зависит от схемы соединения элементов и в рассматриваемом случае в соответствии с [6; 8] и выражением (1) при q ₁( t ) = 1 определится как

11 t = =       = 166,6 ч.

• ¹ N ⋅ω 60 ⋅ 1 ⋅ 10 ^{- 4}

Следует отметить, что эта расчетная наработка на отказ элемента в системе близка к наработке элементов в системе Ту-154М, определенной по эксплуатационным данным.

Параметр потока отказов элемента системы определяется его средней наработкой на отказ ω= . t cp

При этом t _ср определяется по результатам испытания большой совокупности однотипных элементов по плану испытаний с восстановлением. Таким образом, t ср является статистически средним для функции распределения вероятности отказа элементов q* ( t ) (см. рисунок). При распределении равномерной плотности, диапазон возможных наработок элементов на отказ изменяется от 0 до 2 t ср .

Авиационные элементы изготавливают на сертифицированных предприятиях по сертифицированным технологиям. Элементы, устанавливаемые в системы самолета при комплектовании или замене отказавших, берутся из партии случайным образом. При этом в системе с одинаковой вероятностью могут устанавливаться элементы с различными наработками на отказ, изменяющимися в диапазоне от 0 до 2 t ср .

Допустим, что в системе, при сохранении ω_Σ неизменным, установлен один из наугад выбранных элементов, имеющий наработку на отказ, равную t_i = 1 ч. Вероятность события P ₁ , выбора наугад из всей партии элементов именно такого элемента, определится как

P = ^ti

¹    2 t cp

.

Поскольку в рассматриваемой системе-аналоге 60 элементов, вероятность события P ₆₀ , попадания в нее такого элемента, выше и равна

P 60 ⁼

60 ⋅ t_i 2 t _cp

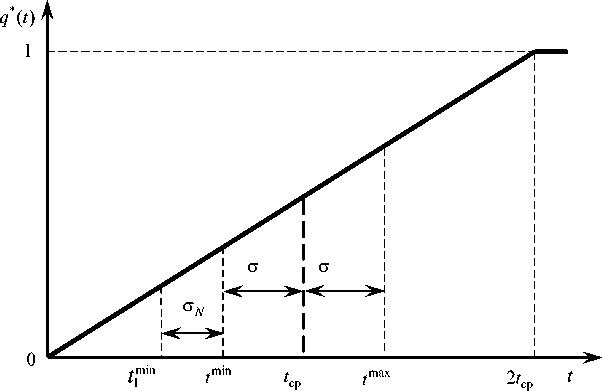
Схема учета среднеквадратических отклонений при определении минимальной наработки на отказ элемента системы

Поскольку рассматриваемый элемент с вероятностью, равной q ( t ) = 1, отказывает не в точке времени t_i , а на интервале [0, t_i ], то естественно допустить, что он откажет в середине этого интервала, т. е. за время t = 0,5 ⋅ t_i . Отсюда вероятность отказа рассматриваемого элемента на отрезке [0, t_i ] будет

q ( t i ) = _0, ^P ₅ ⁶⁰ _{⋅ ti} .                     (6)

Тогда время до отказа этого первого элемента в системе, при условии попадания его в ее структуру, составит совокупности. Но поскольку ωcp

ω

^Σ , то и ω и t

N           cp 1

также не зависят от числа N выбираемых наугад элементов.

В теории надежности из экспериментально построенного распределения вероятности отказа q* ( t ) используется только одна его числовая характеристика, это t ср стремящееся к математическому ожиданию. Но если учесть и другую характеристику, т. е. среднеквадратическое отклонение σ, то возможные значения времени до отказа конкретного типа элементов определятся в диапазоне от t ^min до t ^max (см. рисунок), т. е.

0,5 ⋅ t_{i =} t _c p

P 60     60

t min

= t _cp

-σ ,

При 60 элементах, имеющих t _cp = 1 ⋅ 10 ^{- 4} ч, это время составит 166,6 ч, т. е. тоже, что и t ₁, рассчитанное ранее по (3).

Расчеты показывают, что если принять наработку на отказ выбранного наугад элемента системы равной 10, 100 либо 150 ч, то время до отказа первого элемента в системе t 1 останется прежним и равным t 1 = 166,6 ч, как и определено по выражению (3).

Таким образом, в работе рассмотрена процедура вероятностного комплектования системы элементами выбором их наугад. В соответствии с ней, оценивая время до отказа системы с учетом наименее надежного элемента, необходимо в вероятностной постановке учитывать и вероятности реализации события попадания в систему такого элемента. Второй вывод из полученных результатов указывает на то, что время первого отказа в системе t 1 устойчиво к процедуре ее комплектования выбором наугад элементов и определяется суммарным параметром ω_Σ системы по (3) либо средней наработкой на отказ t _ср по (7).

Таким образом, показано, что ω_Σ и t 1 не зависят от процедуры выбора элементов наугад из некоторой

max t= tcp +σ.

Неравенство Чебышева (закон больших чисел) указывает на то, что вероятность отклонений случайной величины от ее математического ожидания может выйти за пределы трех среднеквадратических отклонений не более чем на 1/9. При распределении равномерной плотности вероятность выхода случайной величины за пределы σ составляет 0,71, за пределы 2 σ – 0,42, и за пределы 3 σ – 0,13.

В связи с изложенным проблема определения возможных границ отклонения случайной величины, наработки на отказ элемента, от ее математического ожидания представляется актуальной. Ее решение возможно сопоставлением результатов расчета надежности систем с экспериментальными значениями. Выполненные авторами ускоренные испытания восстанавливаемой системы из ламп накаливания показали приемлемость оценки отклонения 2 σ . При этом для распределения с равномерной плотностью вероятности [9] оценка отклонения примет вид

2 σ= t ^cp

.

Распределение q*(t) определяет надежность одного конкретного типа элементов. Но существует еще рассеяние времени отказов элементов относительно tср, зависящее от числа N выбираемых наугад элементов. Это рассеяние также может быть определено среднеквадратическим отклонением σN . Нетрудно понять, что при N = 1 σN =σ, определяемому по (9), а при увеличении N до бесконечности σN →0 . Тогда при распределении равномерной плотности σN естественно определить как min

σ N = t . (10) 3 ⋅ N

Этот же результат получается при использовании одной из основных теорем теории больших чисел теоремы Чебышева [9]. Таким образом, нами получено подтверждение необходимости использования теоремы Чебышева в расчетах надежности систем.

В системах самолетов используются элементы с различными законами распределения вероятности времени до отказа q_i ^* ( t ). При стационарном процессе эксплуатации q_i ^*( t ) для всех элементов определится распределением равномерной плотности, но со своими числовыми характеристиками t i ср и σ _i . Обобщенная теорема Чебышева для независимых случайных величин доказывает правомерность использования одной из основных теорем закона больших чисел (теоремы Чебышева) и для случаев с различными q_i ^* ( t ) [9]. Для зависимых случайных величин, правомерность использования теоремы Чебышева доказана в теореме Маркова.

Поскольку для систем самолетов, отказы которых приводят к катастрофическим ситуациям, важно знать нижнюю границу оценки надежности, то в расчетах надежности элементов необходимо использовать оба среднеквадратических отклонения: и σ , и σ _N .

Таким образом, вначале необходимо для исходного распределения q*(t) конкретного типа элементов определять среднеквадратическое отклонение и минимальное время до отказа как min t=tcp

t cp

.

Поскольку tср и tmin не зависят от N, то затем следует учитывать Чебышевское среднеквадратическое отклонение для элементов системы, с учетом их числа в системе. Например, для рассматриваемого случая при равенстве средних наработок на отказ всех элементов минимальное время до отказа первого элемента в системе определится как min t1

₌ t min

t min

. 3 N

Тогда с учетом среднеквадратических отклонений σ и σN значение параметра потока отказов элемента, используемое для расчета надежности систем, следует определять в виде

ω= 1 . (13) min t1

Таким образом, показано, что в расчетах надежности систем, при определении параметра потока отказов, необходимо учитывать как значение средней наработки элементов на отказ, определенное по результатам их испытаний, так и среднеквадратическое отклонение этой наработки. Кроме того, поскольку при комплектовании системы элементы из партии берутся наугад, то в расчете надежности системы необходимо учитывать среднеквадратическое отклонение, зависящее от числа элементов в системе и определяемое одной из основных теорем закона больших чисел (теоремой Чебышева).