О валидации модели движения людей SIgMA.CA по данным фундаментальных диаграмм

В наши дни вопрос безопасной эвакуации людей из зданий и сооружений становится все более актуальным. Поэтому возникает потребность в математических моделях движения людей, например, с целью определения наилучшей геометрии пространства, где предполагается скопление и задержка движения, определения времени эвакуации и т. д.

движения людей, валидация модели, фундаментальная

Несмотря на то, что существует достаточное количество как коммерческих предложений подобных моделей, так и научных исследований в этой области [1; 2], продолжение исследований остается востребованным из-за сложности рассматриваемого процесса (движение людей) и вариабельности натурных данных.

Вопросы валидации и верификации моделей являются одними из самых важных. На сегодняшний день единственным качественным способом верификации моделей движения людей является построение фундаментальной диаграммы (ФД). ФД – это кривая, отображающая зависимость скорости человека от плотности или потока от плотности. В то же время, диаграммы, полученные разными учеными в разных странах и в различных условиях, могут отличаться друг от друга в силу того, что движение человека обусловлено многими факторами, зависит от окружающей обстановки и психологического состояния. Тем не менее, у всех ФД есть одно общее свойство: с ростом плотности поток растет и, достигнув максимума при определенном значении плотности, начинает убывать; скорость уменьшается с ростом плотности.

Обычно данные замеряются на прямом участке пути. В литературе утверждается, что повороты не влияют на движение людей, однако не приводятся ни качественные, ни количественные доказательства этого утверждения [3]. При малых плотностях потока или небольших скоростях это, действительно, так. Но с другой стороны, если скорость достаточно велика, то при совершении поворота она уменьшится. Также средние и большие плотности влияют на динамику движения, и поворот не может не сказаться на величине потока. Поэтому возникает вопрос, будут ли ФД, построенные для различных геометрий пространства, совпадать.

В работе рассматриваются ФД, полученные с помощью дискретной стохастической модели SIgMA.CA (Stochastic fIeld Movement of Artificially People Intelligent Cellular Automata model) для двух различных геометрий пространства, и приводится сравнение модельных данных с некоторыми натурными [4] (см. Kirik E., Yurgel'yan T., Krouglov D. On realizing the shortest time strategy in a CA FF pedestrian dynamics model // Cybernetics and Systems. 42:01. 2011 (to appear)). Цель работы – выявить, влияет ли вид пути на ФД, и насколько модельные данные соответствуют натурным.

Модель движения людей SIgMA.CA. Пусть известны геометрия рассматриваемого пространства и начальное расположение частиц (людей) в этом пространстве. Пространство представляет собой плоскость, разбитую на ячейки 40 × 40 см, которые могут быть либо свободными, либо занятыми только одной частицей. В ячейках также могут располагаться стены и другие недвижимые препятствия.

Целью передвижения частиц является ближайший выход. Информацию о местоположении любого выхода дает статическое поле S , которое можно интерпретировать как карту местности [5]. Поле S радиально возрастает от точки выхода, не изменяется со временем и под действием частиц.

На каждом временном шаге частица может переместиться в одну из четырех свободных соседних ячеек или остаться на месте (окрестность фон Неймана). Направление частицы предполагается случайным и определяется на основе вероятностей переходов в каждом направлении для каждой частицы в каждый дискретный шаг времени и набором правил переходов частиц [4].

Правила перехода частиц следующие: сначала рассчитывается поле S , затем на каждом временном шаге вычисляются переходные вероятности и выбирается направление для перехода. Если две или более частицы претендуют на одну и ту же ячейку, применяется процедура разрешения конфликтов: либо все частицы остаются на прежних местах, либо только одной будет позволено переместиться. Стоит отметить, что вероятность перехода в занятую ячейку в общем случае не равна нулю. Частице, выбравшей занятое направление, предоставляется возможность либо выбрать другое направление для перехода, либо остаться на месте и подождать, пока выбранное направление освободится. Правила применяются ко всем частицам в один и тот же момент времени.

При вычислении переходных вероятностей учитывается «карта» расстояний до выходов S , желание частиц двигаться по направлению к выходу и желание держаться на некотором расстоянии от людей и от стен, что обеспечивается соответствующими параметрами модели k_S >  = 0, k_P >  = 0, k_W >  = 0 и радиусом видимости r >  0 (расстояние в количестве ячеек).

Исследования. Рассматривались два примера (рис. 1). Было организовано движение частиц с постоянной плотностью p [1/м²], частицы равномерно располагались по всему пространству. Замерялось время T (в шагах), за которое через сечение пройдет определенное количество частиц N (для прямого коридора N = 1 000, для коридора с поворотами N = 200) для заданной плотности потока.

Параметры модели k S и k W были фиксированными, и k S = k W = 4 (параметр k S = 4 соответствует направленному движению частиц), параметры k P и r изменялись. Рассмотрим следующие пары: k P = 2 и r = 1, k P = 4 и r = 1, k_P = 4 и r = 10, k_P = 12 и r = 10.

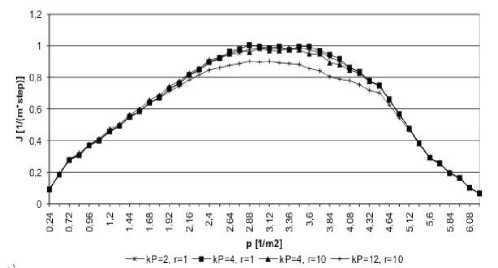
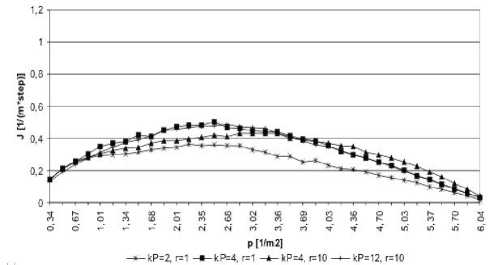
По полученным данным был вычислен поток J _мод = N/T/2 [1/(м∙шаг)] и построены ФД (рис. 2), которые показывают, что модель чувствительна к изменению вида пути (прямой или с поворотами).

На малых плотностях (при p < 1 [1/м²]) ФД совпадают, но на средних – поток для примера 2 (рис. 2, б ) в два раза меньше потока для примера 1 (рис. 2, a ). Это означает, что в прямом коридоре скорость движения выше, чем в коридоре с поворотами.

Плотность, при которой J мод достигает максимального значения, для примера 1 больше, чем для примера 2 (почти всегда) (см. таблицу). Значение p ( J _max) интерпретируется как величина плотности, после которой передвижение людей становится затруднительным и падает скорость движения. Таким образом, в прямом коридоре частицы двигаются быстрее при большей плотности.

времени

а

б

Рис. 1. ФД, построенные по модельным данным: а – пример 1; б – пример 2

б

Рис. 2. Фундаментальные диаграммы: а – для примера 1; б – для примера 2

Значения p ( J _max ) для примеров 1, 2

p ( J max ), 1/м	kP = 2, r = 1	kP = 4, r = 1	k P = 4, r = 10	k P = 12, r = 10
Для примера 1	3,44	2,88	2,96	2,88
Для примера 2	2,18	2,52	3,19	2,68

Параметры модели определяют динамику модели и оказывают влияние на величину потока [4]. Например, параметры, которые соответствуют максимальному по величине потоку для примера 1 ( k P = 2, r = 1), для примера 2 дают минимальное значение потока (см. таблицу). Это объясняется влиянием параметров на динамику движения, но этот вопрос в данной статье обсуждаться не будет. Отметим только, что для прямого коридора наилучшими параметрами с точки зрения реалистичности динамики движения будет пара k_p = 2, r = 1, для коридора с поворотами – k_P = 4, r = 10 и k_P = 12, r = 10, на малых плотностях достаточно хорошие результаты могут быть и при k_P = 4, k P = 2 и r = 1.

Сравнение ФД, полученных по модельным и натурным данным. В качестве натурных использовались данные Предтеченского и Милинского (PM) [6], Вейдманна (WM) [7] и Зейфрида (Seyfried) [8]. В первом и во втором случае данные получены на прямых участках пути, данные Зейфрида – на замкнутом контуре формы овала. Отметим, что в экспериментах Вейдманна и Зейфрида люди двигались медленнее (поток ниже), чем у Предтеченского и Милинского.

Для сравнения модельных и натурных данных требуется приведение к единым единицам измерения. Напомним, что за один расчетный шаг частица может передвинуться на 40 см, поэтому единица измерения потока 1/(м∙шаг) переводится в 1/(м∙с) по формуле J = N/ ( T∙ 0,4 /V ) / 2, где V – скорость движения потока (экспериментальные данные), соответствующая данной плотности.

На рис. 3 отражены полученные результаты, приведены потоки для экспериментальных данных и модельных расчетов. В случае прямого коридора наблюдается совпадение расчетных и экспериментальных значений потоков для малых и средних плотностей (примерно до плотности 2,88 1/м2). Поэтому можно утверждать, что на таких плотностях в целом динамика потока, воспроизводимая моделью, совпадает с имеющей место в натурных экспериментах.

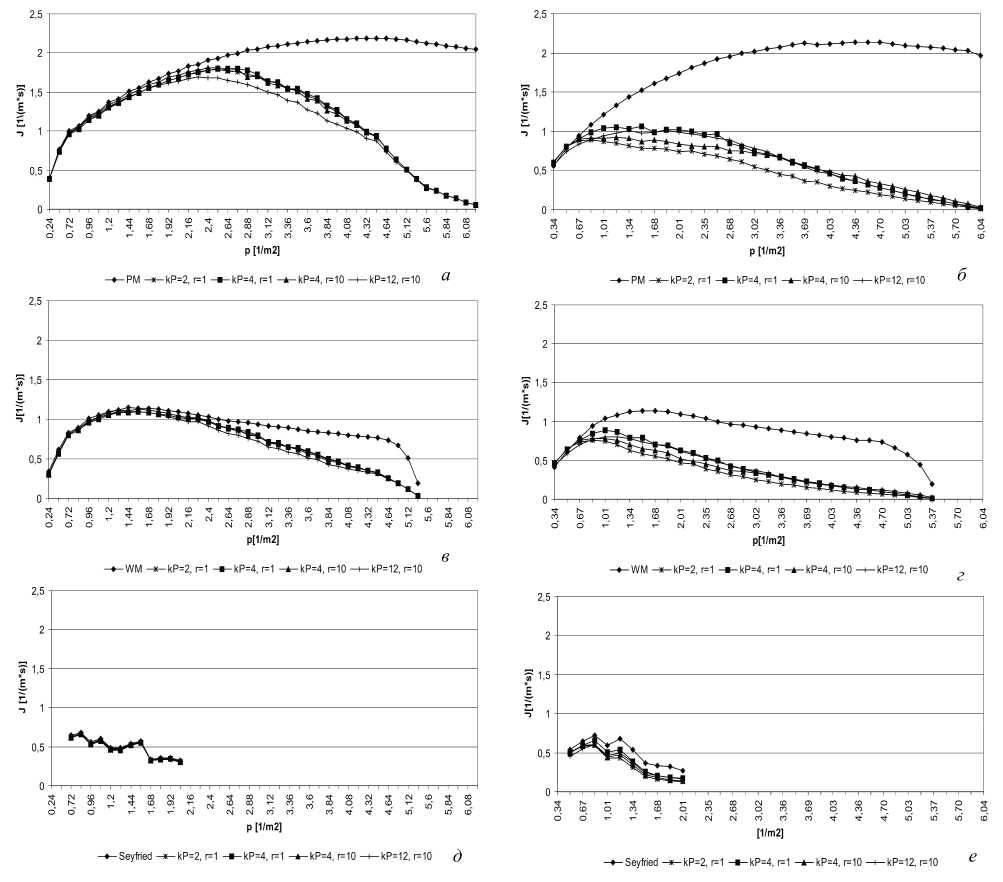
Рис. 3. Фундаментальные диаграммы, вычисленные с помощью различных натурных данных: PM – данные Предтеченского и Милинского, WM – Вейдманна и Seyfried – Зейфрида;

a , в , д – для примера 1; б , г , е – для примера 2

С дальнейшим ростом плотности динамика модели замедляется. Причем, чем медленнее экспериментальная скорость, тем при больших значениях плотности начинаются существенные расхождения модельных и экспериментальных кривых.

В случае движения по замкнутому кругу, чем медленнее экспериментальная скорость, тем меньше величина расхождения между модельными и экспериментальными данными. Причем кривые начинают расходиться уже при плотности 0,84 1/м2, т. е. при достаточно свободном движении. Наилучшее совпадение для данной формы пути наблюдается с данными Зейфрида, которые получены также на пути замкнутой формы.

Анализ и сравнение результатов для разных форм пути (рис. 3, a, б, в, г соответственно) показывают следующее. Экспериментальные и модельные кривые, полученные в схожих условиях (рис. 3, a, в), совпадают при малых и средних плотностях, но отличаются на тех же плотностях на рис. 3, б, г. Из этого факта можно сделать вывод, что наличие поворотов все же имеет влияние на динамику людского потока. Этот тезис подтверждает рис. 3, е, где происходит сравнение с натурными данными, полученными на замкнутом контуре, и имеется наибольшее совпадение.

Таким образом, можно сделать следующие выводы:

– модель чувствительна к виду пути: при наличии поворотов поток уменьшается примерно в два раза по сравнению с прямым участком;

– отсутствие натурных данных для геометрий, подобных примеру 2, не позволяет делать полноценные выводы об адекватности модели;

– необходимы дополнительные натурные эксперименты.