О вейвлет-спектрограммах рядов Кондратьева

Введение . Хорошо известно, что Н.Д. Кондратьев впервые установил существование многолетних циклов в статистических рядах, образованных различными экономическими данными [1; 2]. При этом он исследовал статистические ряды, которые характеризуют временную зависимость различных типов данных (элементов), включающих в себя:

• 1)    элементы ценностного характера, например процент на капитал, заработная плата, вклады в банки и т.д.;

• 2)    элементы смешанного характера, т.е. слагающиеся под влиянием изменения как ценностных, так и натуральных факторов, например объем внешней торговли в ценностном выражении;

• 3)    элементы чисто натурального характера, например данные о продукции различных отраслей промышленности и потреблении различных товаров.

Проведенный им анализ показал, что во всех этих рядах можно обнаружить общую закономерность, заключающуюся в существовании глобальных циклов, периоды которых в среднем составляют ~50-55 лет. Заметим, что такой вывод Н.Д. Кондратьев сделал не в результате прямого анализа соответствующих рядов, а путем исследования предварительно обработанных статистических рядов. Предварительная обработка рядов заключалась в следующем.

• 1.    Исходному ряду ставился в соответствие некий «средний» ряд, получающийся из исходного ряда путем эмпирического выделения (подбора).

• 2.    Строился ряд (разностный), представляющий собой разность исходного и «среднего» рядов.

• 3.    Колебания разностного ряда и являлись предметом исследования Н.Д. Кондратьева.

Анализируя колебания разностного ряда, Н.Д. Кондратьев пришел к выводу о том, что существуют большие циклы экономической конъюнктуры [1; 2].

Очевидный недостаток такого подхода связан с тем, что он содержит элемент произвола, заключающийся в эвристическом определении «среднего ряда». Это обстоятельство и было предметом критики еще в 1925 г. [3, с. 234–237].

В настоящей работе показано, что расчет вейвлет-спектрограмм для необработанного ряда Кондратьева позволяет выделить не только крупномасштабные, но и мелкомасштабные циклы. Кроме того показано, что наилучшие результаты получаются при использовании вейвлетов Добеши высокого уровня.

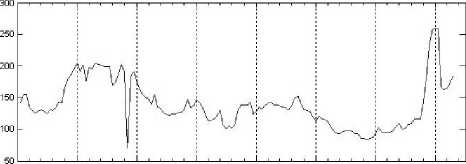
Постановка задачи. Рассмотрим ситуацию, когда исходный временной ряд образован временным ходом данных – индексом товарных цен, выраженным в золоте, по Англии [1]. Заметим, что использованные нами данные для индекса товарных цен за период с 1780 по 1925 гг. заимствованы непосредственно из таблиц самого Н.Д. Кондратьева [1, с. 358–360]. Графическое изображение этого ряда, полученное на основе линейной интерполяции данных, представлено на рис. 1. Из данных, представленных на этом рисунке, следует, что для изображенной на рис. 1 кривой характерны разномасштабные колебания с переменной амплитудой.

Англия: индекс товарных цен, выраженный в золоте

1800       1820       1840        1860        1880        1900        1920

Рис. 1. Англия: индекс товарных цен, выраженный в золоте

Заметим, что для анализа данных, представленных на рис. 1, можно применить как гармонический анализ на основе дискретного преобразования Фурье (ДПФ), так и дискретного вейвлет-преобразования (ДВП). Однако в нашем случае предпочтительным является использование вейвлет-преобразования с построением вейвлет-спектрограмм (аналогом частотного спектра в ДПФ), поскольку такая спектрограмма дает возможность определить не только на- личие разномасштабных колебаний, но и их временную локализацию [4].

Хорошо известно, что для построения вейвлет-спектрограмм можно использовать вейвлеты различных типов. Поэтому сначала необходимо было исследовать спектрограммы, получаемые с помощью различных типов вейвлетов. В работе мы использовали шесть различных типов вейвлетов: Хаара, Добеши 10 уровня, До-беши 30 уровня, Морле, койфлеты Койфмана 5 уровня и Симлета 7 уровня (см. [4] и приведенную литературу). Алгоритм построения спектрограмм на основе указанных вейвлетов был реализован в среде MATLAB.

На рис. 2 представлено графическое изображение рассчитанной спектрограммы для ряда индекса цен (рис. 1), полученных на основе вейвлетов Хаара. Рис. 3а, рис. 3б иллюстрируют результат применения вейвлетов Добеши 10 уровня и Добеши 30 уровня, соответственно. Рис. 4 – рис. 6 изображают результат расчета спектрограммы на основе вейвлетов Морле, Койфмана 5 уровня и Симлета 7 уровня, соответственно. При этом по горизонтали (ось x ) отложено время (единица измерения – год), а по вертикали (ось y ) – интенсивность (амплитуда) соответствующего периода колебаний. Таким образом, по расстоянию между максимумами интенсивности можно определить период колебаний.

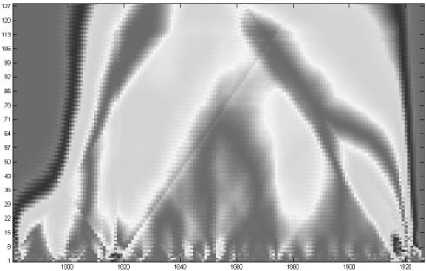
Рис. 2 Спектрограмма на основе вейвлетов Хаара

а)

б)

Рис. 3. Спектрограмма на основе вейвлетов Добеши

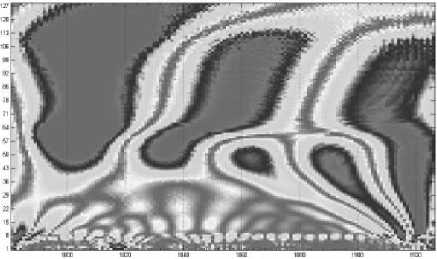
Рис. 4. Спектрограмма на основе вейвлетов Морле

Рис. 5. Спектрограмма на основе вейвлетов Койфмана 5 уровня

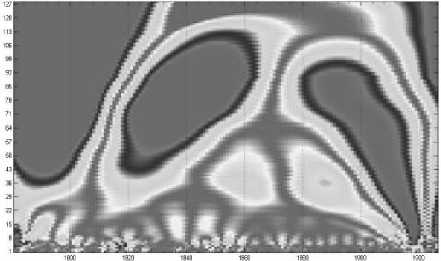
Рис. 6. Спектрограмма на основе вейвлетов Симлета

Из приведенных на этих рисунках данных можно сделать следующие выводы.

• •    Все спектрограммы имеют похожую структуру.

• •    У всех спектрограмм наблюдается наличие периода 48–50 лет.

• •    Различия в структуре спектрограмм наблюдаются как для их среднемасштабных областей, так и для мелкомасштабных областей.

• •    Наибольшей детализацией обладают вейвлеты Добеши 30 уровня.

• •    Распределение периодов в области самых мелких масштабов носит скорее случайный характер, чем регулярный.

Таким образом, мы установили, что прямой расчет спектрограмм для временного ряда (индекса товарных цен) на основе вейвлетов дает возможность определить у него как крупномасштабные, так и среднемасштабные и мелкомасштабные циклы конъюнктуры. При этом предпочтительно использовать вейвлеты Добеши 30 уровня. Кроме того, поскольку спектрограммы получены без какой-либо предварительной эвристической обработки исходного ряда, то полученный результат можно рассматривать как доказательство существования циклов Кондратьева.