О влиянии диагональных компонентов тензора скоростей деформации на ламинарный пограничный слой на плоской пластине
Автор: Никонов В.В., Шахов В.Г.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 5-1 т.11, 2009 года.
Бесплатный доступ
Рассматривается прямое численное моделирование ламинарного пограничного слоя на плоской пластине в широком диапазоне чисел Рейнольдса. Используется метод конечных разностей. Применяется схема интегрирования с разными шагами по времени из-за разности скоростей протекания процессов диффузии и конвекции. Исследуются два варианта постановки задачи с упрощенным и полным представлением члена, отвечающего за вязкую диффузию. Полученные профили скорости сравниваются с решением Блазиуса и результатами схемы метода расщепления завихренности (МРЗ). Отмечается, что, несмотря на одинаковый порядок точности решения, метод конечных разностей в 20 раз более медленный, чем МРЗ.
Пограничный слой, плоская пластина, численный метод, число рейнольдса, диффузия, конвекция, тензор скоростей деформации, решение блазиуса
Короткий адрес: https://sciup.org/148198687
IDR: 148198687 | УДК: 532.526
Текст научной статьи О влиянии диагональных компонентов тензора скоростей деформации на ламинарный пограничный слой на плоской пластине
1. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА МЕТОДА
Математическая формулировка задачи описывается уравнениями Навье-Стокса. Давление в ламинарном пограничном слое на плоской пластине мало меняется, поэтому будем считать его постоянным. Рассматривается два варианта постановки задачи с упрощенным du 5 u 5 u
--+ u--+ v--= V--7 51 5 x 5 y
5 v 5 v 5 v
--+ u + v = V 2 (1) 51 5x 5y и полным du 5 u
--+ u--+ v— = V 51 5 x f a 2u d 2u ) '.-
^5 x d y J
d v d v 5 v ( d S d 2 v
— + u — + v— = v —7 + —7 a t a x a y (5 x2 a y J представлением члена, отвечающего за вязкую диффузию. Здесь используются безразмерные переменные: u = u*/u , v = v*/um - компоненты скорости, v = V fu . b = VRe – безразмерный коэффициент кинематической вязкости, x = x*/b, y = y*/b – безразмерные координа-
ты, t = t * b/u „ - безразмерное время, где b -длина пластины, u m - скорость набегающего потока. Упрощение системы (2) заключается в отбрасывании диагональных компонентов тензора скоростей деформации.
Для замыкания системы уравнений необходимо добавить уравнение неразрывности, которое для несжимаемой жидкости имеет вид
5 u 5 v dx+dy=0. (3)
Переопределенность системы (1)-(3) в численном методе преодолевается следующим образом. Сначала решаются уравнения (1) или (2). Затем компонента v скорости корректируется так, чтобы поле скорости удовлетворяло уравнению неразрывности (3).
По аналогии с методом расщепления завихренности [1] изменение скорости в (1) или (2) вследствие конвекции и диффузии рассматривается отдельно, т.е. производится расщепление по физическим процессам.
На этапе конвекции решается следующая конечно-разностная система уравнений:
ui,j - u^ - /9u\ vt 9u\
_- ui,j\^ - vi,j\^/
A tc \9x/i,j \9 y/i,j , vt+jAt -vt,j - /9VV /9vV
"- ui,j\ dx . - vi,j\ d y ,(4)
A c \ / i,j \ v / i,j где Atc - шаг по времени для процесса конвекции, а для аппроксимации частных производных по пространству применяется конечно-разностная схема “вперед по потоку” 2-го порядка
дх/ 2h(3u i,j 4u i - i,j + u 2' )’ u i + i/2,j ~0’u i - i/ 2 ,j “0
xi,j fu/ = ^ ( ui+1,j-ui-1,j) ’ ui+1/2,j- 0’ui-1/2,j< 0
x i,
=2^(-ui+2,j +3ui+1,j -3ui-1,j +ui-2,j)’ ui+1/2,j <0’ui-1/2,j >0, xi, lx/ =-2h f3u 4u- ' ui+2’j) ’ ui+1/2’j< 0’ui-1/2,j^ 0 (5)
где величины компонент скорости u i+1/2, j и u i-1/2, j определяются как
u i,j + Ui + 1,j u i + i/2,j = —2— , u
'i - 1/2,j -
u i - 1,j + u i,j _
2 , (6)
а h – размер ячейки однородной расчетной сетки. Для ячеек вблизи плоской пластины и внешних границ расчетной области применялась конечно-разностная схема “вперед по потоку” 1го порядка
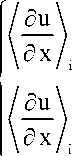
ui’j- ui-1,j h ui+1,j- ui’j h
i,j
u .,j < 0 .
Граничные условия (ГУ) прилипания потока на поверхности пластины на этапе конвекции для слоя фиктивных ячеек j-1, находящихся с “обратной стороны” пластины, сводятся к
U i,j - 1 = 0 , (8)
где ячейка с координатами (i, j) является прилегающей к поверхности пластины.
На этапе диффузии используется схема ВВЦП [2], которая для системы (2) будет иметь следующий вид
для слоя фиктивных ячеек j-1, находящихся с “обратной стороны” пластины, сводятся к ui,j-i =-Ui,j, (10)
где ячейка с координатами (i, j) является прилегающей к поверхности пластины.
В работе [3] было показано, что для достижения заданной точности шаг по времени для схемы ВВЦП определяется следующим соотношением
A t = k d h2/ v , (11)
где kd – константа, от которой зависит ошибка численного решения. Минимальная ошибка получается при kd = 0,22.
Шаг по времени для процесса конвекции удовлетворяет неравенству
A t c ^ 0.1h , (12)
для критерия Куранта-Фридриха-Леви [4], равного 0,1, который получен для схемы (4), (5) серией численных расчетов. При этом он не обязательно совпадет с оптимальным шагом для расчета процесса диффузии. По этой причине предлагается применять метод интегрирования с разными шагами по времени (ИРШ) для процессов диффузии и конвекции.
Корректировка поля скорости для удовлетворения уравнения неразрывности (3) производится на этапе конвекции перед расчетом (4). Для каждой ячейки сетки вниз по потоку профиль скорости будет менее заполненным, чем для предыдущей ячейки, вследствие развития пограничного слоя. Это приводит к тому, что в каждую ячейку сетки в продольном направлении втекает больше жидкости, чем вытекает из нее. Поэтому предполагается, что избыточное количество жидкости вытекает в поперечном направлении, вызывая тем самым появление вертикальной компоненты скорости течения.
Из (3) можно записать
5 v
= .(13)
5 y 5 x
t+ Д t u
- U t:
A t d
=v
t u i" 1 ,!
2u t,j + u t+i,j
t t + A t
-
i,j
к
h2
+
ut,j-1
2u t,j + u t,j+1
h2
( vl
-
к
У
Тогда, согласно (13) и ГУ непротекания на поверхности пластины (v = 0), вертикальная компонента скорости для ячеек, прилегающих к пластине сверху, находится следующим образом:
A t d
=v
- 4 + v i + l’J
к
h2
+■
v j
- 2vi,j + vi,J + i
h2
к
,
У
du vi,j 0.5н.^_ ;
d x i,j
.
(9) где A td - шаг по времени, необходимый для процесса диффузии. Для системы (1) схема (9) соответствующим образом упрощается.
Граничные условия (ГУ) прилипания потока на поверхности пластины на этапе диффузии
Для остальных ячеек, расположенных над пластиной, вертикальная компонента скорости определяется как
• i,j = v i.j - 1 - 0.5h y
/ 5 u
\ 5 x ..
к ' ' i,j
/ du \+ \ /
5 x
' ' i,j - 1 у
. (15)
Для аппроксимации пространственных производных в правых частях выражений (14), (15), как и в [1], использовалась центральная конечно-разностная схема. Формулы для ячеек, расположенных с нижней стороны пластины, получаются зеркальным отражением (14), (15) относительно оси абсцисс OX.
2. ПРЯМОЕ ЧИСЛЕННОЕ
МОДЕЛИРОВАНИЕ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ НА ПЛОСКОЙ ПЛАСТИНЕ
Рассматривается задача о продольном обтекании плоской пластины для того, чтобы проверить диффузию с поверхности тела совместно с моделированием процессов диффузии в свободном потоке и конвекции. Данная задача имеет точное в рамках теории пограничного слоя решение, полученное Блазиусом для ламинарного случая, которое хорошо подтверждается в эксперименте [5]. Известно, что с помощью введения безразмерной нормальной координаты
* η=y
u ∞
Л * *\νx
и величины вертикальной компоненты скорости
v f
** v u ∞ x
А *
u ∞ ν
профили компонент скорости u и vf в разных сечениях пластины x = const будут совпадать, что является удобным для сравнения получаемых данных.
Сравнение профилей скорости с решением Блазиуса производилось для четырех сечений на расстояниях xп ≈ 0.25, xп ≈ 0.5, xп ≈ 0.75 и xп ≈ 0.9 от переднего края пластины.
Расчеты проводились в диапазоне чисел Рейнольдса от 10 до 10 5. Параметры численного мо-
делирования приведены в табл. 1. Здесь te – конечное безразмерное время счета, Tm – затраты машинного времени в часах, минутах и секундах для решения систем уравнений (1) и (2), L и H – размеры расчетной области вдоль координат x и y соответственно, nx и ny – число ячеек сетки вдоль координат x и y.
Видно, что необходимый шаг расчетной сетки пропорционален квадратному корню из безразмерной кинематической вязкости n. Это условие вытекает из обратной пропорциональности толщины ламинарного пограничного слоя корню квадратному из числа Рейнольдса. Также следует отметить существенный рост потребного машинного времени при увеличении числа Рейнольдса (табл. 1), так для числа Re = 10 5 расчеты длились более 2 суток. Заметим, что результаты данной работы получены на компьютере с частотой процессора 3.2 ГГц и 1 Гб оперативной памяти, который является в 2.6 более производительным, чем компьютер, который использовался в работе [1]. Сравнивая время счета для Re = 1000 и h = 0,01, приведенное в табл. 1, со временем счета для МРЗ в работе [1], можно заключить, что рассматриваемый в данной работе метод является в 20 раз более медленным, чем МРЗ. Это происходит потому, что на этапе конвекции в рассматриваемом методе приходится использовать в 15 раз более мелкий шаг (12), чем в схеме МРЗ.
В результате моделирования задачи было выявлено, что в диапазоне чисел Рейнольдса от 100 до 10 5 для систем (1) и (2) получаются одинаковые результаты (таблица 2), за исключением профиля вертикальной компоненты скорости для сечения xп ≈ 0.9 при Re = 100 (см. рис. 1). Заметим, что для вертикальной компоненты скорости удается достичь достаточной для инженерных целей точности лишь на более мелких сетках (табл. 2). При числе Re = 10 для системы (1),
Таблица 1. Параметры численного моделирования пограничного слоя в зависимости от числа Рейнольдса
|
Re |
h |
LxH |
Пх X ny |
д1<1 |
д1с |
Tm, [чч:мм:сс] |
||
|
(1) |
(2) |
|||||||
|
10 |
0.1 |
4x8 |
40x80 |
0.022 |
7.333333-10"3 |
16.8 |
00:00:08 |
00:00:12 |
|
0.05 |
4x8 |
80x160 |
5.5-Юч |
2.75-10 3 |
16.8 |
00:01:28 |
00:02:22 |
|
|
0.025 |
4x8 |
160x320 |
1.375-10"3 |
1.375-10 3 |
16.8 |
00:13:57 |
00:15:32 |
|
|
100 |
0.03125 |
4x4 |
128x128 |
0.021484 |
3.069196-10"3 |
16.8 |
00:01:36 |
00:01:38 |
|
0.015625 |
4x4 |
256x256 |
5.371094 103 |
1.342773-IO3 |
16.8 |
00:32:38 |
00:37:20 |
|
|
103 |
0.01 |
4x2 |
400x200 |
0.022 |
0.001 |
16.8 |
00:25:12 |
00:29:34 |
|
0.005 |
4x2 |
800x400 |
5.5-10"3 |
5.0-10"4 |
8.4 |
02:51:08 |
02:54:33 |
|
|
104 |
0.003125 |
2x0.5 |
640x160 |
0.021484375 |
3.069196-10"4 |
8.4 |
01:24:47 |
01:35:28 |
|
0.0015625 |
2x0.5 |
1280x320 |
5.371094-10"3 |
1.534598-10"4 |
8.4 |
21:30:10 |
21:29:51 |
|
|
105 |
0.001 |
2x0.1 |
2000x100 |
0.022 |
1.0-10"4 |
4.2 |
06:47:54 |
06:45:09 |
|
5-10' |
2x0.1 |
4000x200 |
5.5-103 |
5.0-10 3 |
4.2 |
61:49:26 |
64:02:59 |
|
Таблица 2. Средняя ошибка численного решения при моделировании пограничного слоя на плоской пластине для профилей скорости в центральном сечении xп ≈ 0.5
|
Re |
h |
5U |
5V |
||||
|
MP3 |
(1) |
(2) |
MP3 |
(1) |
(2) |
||
|
10 |
0.1 |
0.04 |
0.04 |
0.50 |
0.14 |
0.12 |
0.86 |
|
0.05 |
0.02 |
0.02 |
0.38 |
0.06 |
0.06 |
0.74 |
|
|
0.025 |
0.01 |
0.01 |
0.34 |
0.05 |
0.05 |
0.72 |
|
|
100 |
0.03125 |
0.02 |
0.02 |
0.02 |
0.11 |
0.12 |
0.10 |
|
0.015625 |
0.01 |
0.006 |
0.01 |
0.01 |
0.03 |
0.03 |
|
|
103 |
0.01 |
0.01 |
0.01 |
0.009 |
0.10 |
0.10 |
0.10 |
|
0.005 |
0.007 |
0.001 |
0.0008 |
0.02 |
0.01 |
0.01 |
|
|
104 |
0.003125 |
0.01 |
0.007 |
0.007 |
0.09 |
0.08 |
0.08 |
|
0.0015625 |
0.006 |
0.004 |
0.004 |
0.02 |
0.01 |
0.01 |
|
|
105 |
0.001 |
0.03 |
0.006 |
0.006 |
0.13 |
0.20 |
0.17 |
|
5-10"4 |
0.009 |
0.005 |
0.005 |
0.03 |
0.01 |
0.01 |
|
О 1 2 3 4 5 6 Г| 0 1 2 3 4 5 6 ^
а) система (1) б) система (2)
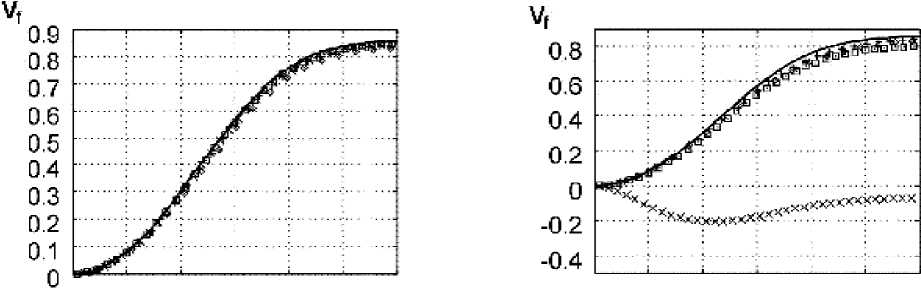
Рис. 1. Профиль вертикальной скорости на плоской пластине, Re = 100, Δ td = 5.371094 ⋅ 10-3, Δ tc = 1.342773 ⋅ 10-3, t = 16.8, h = 0.015625, LxH = 4x4;
– профиль Блазиуса [5], настоящая работа: О – xп = 0.25, + – xп = 0.5, D – xп = 0.75, X – xп = 0.9
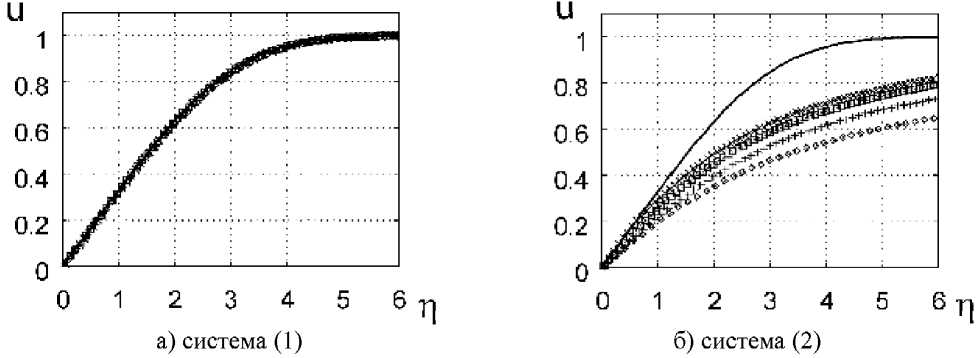
Рис. 2. Профиль продольной скорости на плоской пластине, Re = 10, Δtd = Δtc = 1.375⋅10-3, t = 16.8, h = 0.025, LxH = 4x8; – профиль Блазиуса [5], настоящая работа: О – xп = 0.25, + – xп = 0.5, D – xп = 0.75, X – xп = 0.9
как и для МРЗ в [1] (МРЗ просто другой метод решения системы (1)), удается получить с точностью, достаточной для инженерных целей,
профиль Блазиуса, см. рис. 2.
Погрешность решения, приведенная в табл. 2, определялась следующим образом:
δ= max u 0 ≤η≤ 6
u ex
u i,j - u ex
|
δ v = max 0 ≤η≤ 6 |
v - v i,j ex |
, (17) |
|
v ex |
где uex и vex – поле скорости точного решения Блазиуса.
Для системы (2) при Re = 10 наблюдается сильное отличие численного решения от решения Блазиуса (рис. 2), что объясняется влиянием диагональных компонентов тензора скоростей деформации. Для окончательного вывода не хватает данных эксперимента о продольном обтекании плоской пластины для данного числа Рейнольдса.
Список литературы О влиянии диагональных компонентов тензора скоростей деформации на ламинарный пограничный слой на плоской пластине
- Никонов В.В., Шахов В.Г., Схема расчета скорости для метода "вихрь в ячейке" применительно к моделированию двумерного ламинарного пограничного слоя//Известия СНЦ РАН. 2005. Т. 7. № 2. С. 392-398.
- Флетчер К. Вычислительные методы в динамике жидкостей/Пер. с англ. М.: Мир. Т. 1, 1991. 504 с.
- Никонов В.В. О выборе шага по времени в схеме ВВЦП при расчете процесса диффузии//Сборник трудов 13-го Всеросс. семинара по управлению движением и навигации ЛА. Самара: СГАУ, 2007. Ч. 2. С. 55-57.
- Ferziger J., Peric M. Computational methods for fluid dynamics//3 rev. ed., Springer-Verlag. 2002. 423 p.
- Шлихтинг Г. Теория пограничного слоя/Пер. с нем. Г.А. Вольперта, под. ред. Л.Г. Лойцянского. М.: Наука, 1974. 712 с.


