О влиянии движения на сигнал с гиперболической частотной модуляцией

Цитирование: Шостак С. В. О влиянии движения на сигнал с гиперболической частотной модуляцией / С. В. Шостак, А. В. Бенгард, Г. В. Дорофеев, П. А. Стародубцев // Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(7). С. 783–788. EDN: EFVNIS

Как известно, корреляционная обработка сигнала, или обработка с помощью согласованного фильтра, основана на сравнении отраженного эхо-сигнала с сигналами, которые могли бы быть приняты. Эта задача решается достаточно просто, когда цель неподвижна, так как в этом случае сигналы, не подлежащие сравнению, составляют множество задержаний копий переданного сигнала. В этом случае приемник производит поиск на этом множестве и определяет задержанные копии, лучше всего коррелирующие с принятым сигналом. При использовании пассивного фильтра этот поиск происходит автоматически. В случае движения цели корреляционный приём значительно усложняется, так как эхо-сигнал может заметно меняться по форме в зависимости от типа движения цели и вида излученного сигнала. По этой причине приёмник должен определять не только задержку принятого сигнала, но и другие его характеристики. Один из способов, позволяющий обойти эти трудности, заключается в использовании инвариантного по отношению к доплеровскому эффекту сигнала, который остается согласованным для фильтра при наличии даже весьма большого доплеровского искажения. Таким сигналом, известным в настоящее время, является сигнал с гиперболической частотной модуляцией, иначе – ГЧМ. Вопросам синтеза и анализа таких сигналов посвящено достаточно большое количество работ [2, 5]. Вместе с тем полученные результаты инвариантности ГЧМ сигналов к доплеровским искажениям основаны на предположении постоянства доплеровского параметра, т.е. относительная скорость сближения (расхождения) с целью должна иметь постоянную величину. В реальной же обстановке такие ситуации бывают довольно редко. Рассмотрим эффект Доплера для ГЧМ сигнала, когда цель имеет постоянную скорость, но движется под некоторым произвольным курсовым углом по отношению к носителю ГАС. В этом случае относительная скорость движения «носитель – цель» может быть аппроксимирована начальной скоростью цели и постоянным ускорением в направлении «ГАС – цель», что ведет к частотному сдвигу ГЧМ сигнала. Будем считать, что цель имеет постоянную скорость и движется в произвольном направлении относительно гидролокатора, как показано на рис. 1.

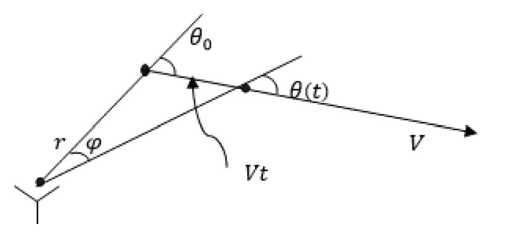
Рис. 1. Движение цели с постоянной скоростью относительно ГАС

Fig. 1. The movement of the target at a constant speed relative to the sonar station

В начальный момент времени угол между вектором скорости цели и направлением на гидролокатор имеет значение θ 0 . В момент времени t , который является длительностью излученного импульса, цель сместится на расстояние Vt и угол будет иметь значение θ_t . Если скорость цели большая и импульс имеет также большую длительность, то значение Vt не постоянно и угол θ изменяется во времени, т.е. является функцией времени θ ( t ). Тогда угол θ ( t ) может быть записан в виде:

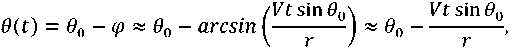
где r – расстояние между ГАС и целью, V – скорость цели.

Скорость изменения расстояния между целью и ГАС имеет вид:

/ ytsin0n\

V_r(t) = V cos 6(t) = V cos (0_O--J.                                (2)

Применяя разложение Тэйлора cos θ ( t ), выражение (2) представим в виде следующего вы-

ражения:

V² sin² 6₀ V³ cos 6₀ ■ sin² 6₀ _

V_r^ ~ V cos 9₀ +--------- ■ t --------- ■ t² + -..

r               zrz

Эта скоростная компонента является результатом доплеровского искажения принятого сигнала, который может быть представлен как функция двух переменных: временной задержкой, вызванной изменением расстояния, и доплеровским масштабом, обусловленным относительной скоростью между ГАС и целью. В этом случае принятый сигнал может быть выражен в виде [5]:

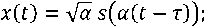
2r т = —, c

«(0

c

где s ( t ) – излученный сигнал, τ – временная задержка, α – доплеровский коэффициент, c – скорость распространения колебаний.

Подставляя выражение (3) в формулу (6) и опуская члены выше второго порядка, получим следующее выражение для доплеровского коэффициента:

2 /          V² sin² 6₀ \ 2У 2У² sin² 6₀

a(t) « 1 — Усо5в₀ H--- t = 1--cos6₀--- t. (7)

c\            r ) c            cr

Из выражения (7) видно, что коэффициент Доплера может быть аппроксимирован добавлением постоянного ускорения к скорости движения цели в основном направлении. При этом значение амплитуды ускорения выражается формулой:

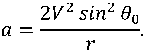
Как известно, сигнал с гиперболической частотной модуляцией (ГЧМ) записывается в следующем виде [1, 3, 4]:

s(t) = A(t)exp p — Zn(l + /c/oO],                                    (9)

где A ( t ) – комплексная огибающая, k – коэффициент модуляции, f ₀ – начальная частота.

Для упрощения выводов произведём сдвиг по времени на величину to ~   , и тогда вы ражение (9) записывается следующим образом:

s(t - t₀) = A(t - t₀) exp — Zn(k/"_ot)j.                              (10)

Подстановка (10) в формулу (4) представляет принятый сигнал как

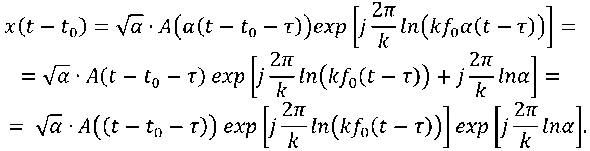
Принимая, что расширение огибающей за счет параметра α незначительно, выражение (11) может быть преобразовано к следующему виду

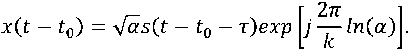
Теперь учтем выражение (7) для параметра α , и тогда принятый сигнал запишется как

x(t — t₀) = Jaslt — t₀ — t) exp

2n / 2У ■ cos0_n

₇ —Zn 1-- к \ c

21/² sin² 6₀

rc

Учитывая также, что возможно приближение

Zn(l + y) « y,

выражение (13) принимает следующий вид:

2л ( xlt — t₀) = ya ■ sit — t₀— т)ехр j' — I —

2V ■ cos0_o 2V² sin² 6₀

c

"    / 2V2 ■ sin260

/2тт-- \ rc / 2V² ■ sin²9₀' j2n------- \ krc

rc

2tt 2V ■ cos0_o

2V ■cos0n t-j2n----- kc

= V« • sit — t_Q — t) exp\jl2nAft + A

2V2 ■ sin260                            2V ■ cos0o где A/ = -           – частотный сдвиг, A(p = —         – фазовый сдвиг.

krc                                  kc

Таким образом, из выражения (15) следует, что принятый сигнал может быть аппроксимирован путем сдвига по времени, частоте и фазе копии излученного сигнала.

При согласованной обработке такого сигнала фазовый сдвиг будет проигнорирован, но частотный сдвиг приведёт к рассогласованию между принятым сигналом и сжимающим фильтром. Поэтому можно создавать сжимающий фильтр путём сдвига частоты копии излученного сигнала. Если угол θ0 неизвестен, то в этом случае необходимо использовать набор фильтров, – 786 – перекрывающих частотный диапазон Δf принятого сигнала. Это будет гарантировать устранение доплеровского искажения.