О влиянии механизма упрочнения на приспособляемость сосуда под давлением в условиях термоциклического нагружения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

В настоящее время передовым направлением российской атомной промышленности является создание замкнутого топливного цикла, сердцем которого должен служить высокотемпературный реактор с жидкометаллическим теплоносителем [1]. Особенность работы подобных реакторов состоит в высоких уровнях механических и температурных нагрузок на корпус реакторной установки, а также циклический характер этих нагрузок в течение эксплуатации энергоблока.

Еще одним ключевым направлением современной отечественной и мировой энергетики является замещение ископаемого топлива в различных высокотемпературных промышленных технологиях. С этой целью активно ведутся разработки отечественного высокотемпературного газоохлаждаемого реактора (ВТГР) с гелиевым теплоносителем, в результате работы которого может быть получено экологически чистое водородное топливо [2]. Разработки такого типа реактора начались в 60-х гг. XX в. в СССР, но до практической реализации доведены не были. Основными преимуществами данного реактора является высокая степень безопасности: нет риска возникновения пароциркониевой реакции, так как в конструкции микротвэлов не используются сплавы с цирконием, а в активной зоне нет воды. Однако в связи с высокой рабочей температурой реактора (более 800 °C) проблемы эксплуатации материалов и расчетного обоснования прочности подобных ответственных конструкций не теряют своей актуальности.

Современные нормы проектирования атомных станций [3; 4] допускают оценку циклической прочности конструкций в условиях неупругого поведения. Упрощенные методики расчета позволяют с определенной степенью консерватизма определять возможность эксплуатации конструкции под действующими проектными нагрузками. Данные методики построены на применении диаграммы Бри [5] для определения характерной приспособляемости сосуда под давлением к термоциклическому нагружению. При таком подходе неупругое поведение материала описывается соотношениями идеальной пластичности.

В случае неудовлетворения критериям циклической прочности по упрощенным методиками допускается проведение последовательных циклических расчетов с учетом нелинейной диаграммы деформирования материала с упрочнением, в результате которых определяется величина накопленной неупругой деформации, которая ограничена нормативными допускаемыми величинами.

Однако нормативные документы не регламентируют тип механизма упрочнения, который должен быть заложен в расчетной модели, что имеет значительное влияние на итоговые величины накопленной неупругой деформации. Настоящая работа посвящена описанию влияния механизма упрочнения материала на приспособляемость сосуда под давлением в условиях термоциклического нагружения. Исследование проводится с применением программного средства конечно-элементного анализа Abaqus .

Механизмы упрочнения материала

Существует три базовых механизма упрочнения: изотропное, кинематическое и смешанное. При циклическом нагружении в случае изотропного упрочнения поверхность текучести изменяет свой радиус при неизменном положении центра в пространстве напряжений. В случае кинематического упрочнения центр поверхности текучести перемещается в пространстве напряжений, но радиус поверхности при этом не меняется (рис. 1) [6; 7].

Видно, что в случае изотропного упрочнения наблюдается значительное увеличение зоны упругого поведения материала (упрочненного) при втором и последующих циклах нагружения, чего не происходит в случае кинематического упрочнения.

В реальном материале наблюдается смешанный механизм, который содержит особенности как кинематического, так и изотропного упрочнения [6; 7]. Сложность использования данного механизма упрочнения в расчетных моделях заключается в необходимости определения параметров составляющих изотропного и кинематического упрочнения на базе ряда натурных испытаний, которые не всегда имеются в распоряжении исследователя для некоторых материалов. Тем не менее для различных марок сталей, из которых выполняются конструктивные элементы реакторов и оборудования атомных станций, известно большое число опубликованных исследований, например [8–13].

Для описания процессов неупругого поведения материала принято использовать закон изменения поверхности текучести Мизеса [15]. Данная модель является наиболее распространенной, используется в опорных для данной работы источниках [8–13] и реализована в большинстве программных комплексов конечно-элементного анализа.

Поверхность Мизеса описывается соотношением:

2 2 (g- X ) : ( с- X ) - R - a^ = 0,       (1)

где с ‘ - девиатор тензора напряжений, a y ₀ - начальный предел текучести материала, X и R – переменные, описывающие эффекты кинематического и изотропного упрочнения соответственно.

Для изотропной составляющей упрочнения закон изменения формы поверхности текучести может быть описан с помощью соотношения в форме закона нелинейного изотропного упрочнения Войса [10]:

Z

R = E R i , R i = b i ( R - ,i~Ri] p ,            (2)

i = 1

где R _{x i} - напряжение насыщения, b_i - скорость выхода на напряжение, p – накопленная пластическая деформация.

Данная форма позволяет с помощью разложения на несколько компонент более точно описывать кривую составляющей изотропного упрочнения. При интегрировании соотношение преобразуется в:

Z

R = E R ~ , i ( 1 - e - b'p ) .                  (3)

i = 1

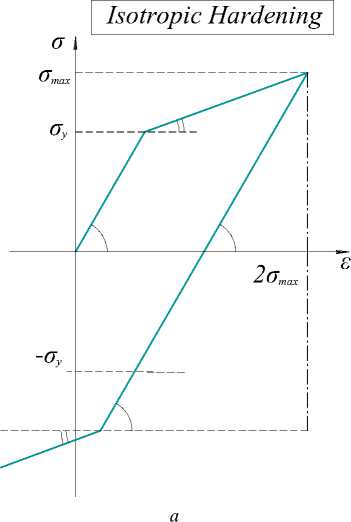
Рис. 1. Механизмы упрочнения на примере одноосного растяжения – сжатия: а – изотропное упрочнение; b – кинематическое упрочнение

Kinematic Hardening

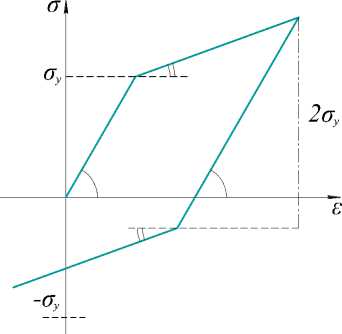
b

Fig. 1. Hardening types in one dimension case: a – isotropic hardening; b – kinematic hardening

В инженерной практике обычно используют одну компоненту ( Z = 1), тогда:

R = R „ ( 1 - e ^- bp ) .                   (4)

В этом случае R „ приобретает однозначный физический смысл – значение асимптоты радиуса поверхности текучести.

Для описания кинематической составляющей упрочнения принято использовать модель Шабоша [15–17], которая может быть представлена в виде соотношений

M

X = £ X i , X_t = -C i e pl - y X p ,        (5)

i = 1                ³

где C_i – модуль упрочнения, γ _i – параметр восстановления, определяющий скорость, с которой модуль упрочнения начинает уменьшаться по мере увеличения накопленной пластической деформации.

Первое слагаемое данного соотношения описывает линейную составляющую кинематического упрочнения по закону Прагера, второе слагаемое описывает мгновенную память формы ( evanescent strain memory ) [15].

Накопленная пластическая деформация p связана с пластической деформацией ε _pl по закону [15]:

p = ^7 ^£ pl ^{: £} pl ,

X в общем случае, является тензором второго ранга обратных напряжений [18], который в английской литературе имеет название back stress tensor . Интегрирование выражения (5) в одномерном случае приводит к виду:

M

X = £ i = 1

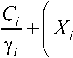
^Ci  I   “ ^ZY i ( ^£ pl ^{- e} pl ,0

^{- Z}--- I e

Y i J

,

где ζ – коэффициент, принимающий значение «1» и «-1» для зоны нагрузки и разгрузки, X_{i ,0} и ε _{pl ,0} – значения начальных напряжений и деформаций.

Современные программные средства численного моделирования ( Ansys, Abaqus, LS-Dyna ) используют модель смешанного упрочнения при Z = 1 и произвольном M [19–21].

Одноосное циклическое растяжение – сжатие образца

Верификация численной процедуры для корректного задания упрочнения в материале под действием циклических нагрузок проводится на базе решения задачи одноосного растяжения – сжатия образца в течение нескольких циклов нагружения. Проводится анализ влияния механизма упрочнения на результирующие диаграммы деформирования. В качестве эталонного источника принимается [12].

В названной работе рассматриваются образцы из стали SA312 TP316. Схожие марки стали по своим характеристикам применяются в элементах высокотемпературных реакторов и сосудов под давлением. В статье [12] проведены экспериментальные исследования по получению монотонной кривой растяжения образца до разрыва и циклические испытания образцов. На базе данных исследований предложены параметры смешанного упрочнения, составляющая кинематического упрочнения которой задана по модели Шабоша [15–17].

Проведение численной верификации проводится в программном средстве Abaqus , в котором заложена аналогичная модель Шабоша [20]. Постановка задачи представлена на рис. 2. U_y на рисунке обозначает вертикальную (в направлении стрелок) компоненту вектора перемещений образца, U_normal – нормальную к поверхности составляющую вектора перемещений.

Кинематическое нагружение U y =A·sin(ωt)

Граничное условие симметрии U normal ⁼ 0

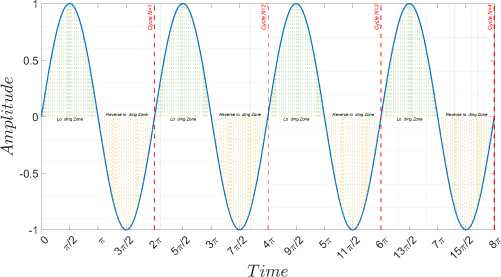
b

Рис. 2. Постановка задачи в программном средстве Abaqus: а – схема нагружения модельного образца; b – временная зависимость изменения амплитуды кинематического нагружения

Fig. 2. Statement of the problem in Abaqus software: a – loading scheme, b – time dependence of the change in the amplitude of kinematic loading

На базе исследования [12] для модели смешанного упрочнения выбираются параметры, представленные в таблице.

Параметры модели Шабоша ([12, табл. 4])

Chaboche model parameters ([12, Table 4])

σ 0 , МПа	С 1 , МПа	γ 1	С 2 , МПа	γ 2	С 3 , МПа	γ 3	R ∞ , МПа	b
116	114783	2000	29935	262	1049	2	178	5.76

Для случая одноосного растяжения в зоне нагрузки на первом цикле нагружения различий в механизмах упрочнения нет, поскольку влияние механизма упрочнения реализуется при смене знака нагружения и повторном нагружении. Подобранные коэффициенты, представленные в таблице, должны в данной зоне в точности совпадать с принимаемой кривой деформирования. На рис. 3 представлено изображение нормативной кривой деформирования и обратных напряжений X для отражения их взаимной зависимости. Анализ соотношения (7) показывает, что уровень напряжений X ниже уровня полных напряжений на величину предела текучести σy,s, что отражено на графике.

На рис. 4 представлены результаты анализа одноосного растяжения (без циклического нагружения) для различных механизмов упрочнения в сравнении с принимаемой кривой деформирования.

Отличие представленных кривых наблюдается из-за различных способов задания механизмов упрочнения в программном средстве Abaqus и некоторой погрешности в процессе определения параметров, что не влияет на точность общих результатов расчета.

Для демонстрации отличия работы различных механизмов упрочнения необходимо проводить циклическое нагружение с фазами нагрузки и разгрузки. Результаты такого исследования приведены на рис. 1, где представлены 1-й, 2-й и 5-й расчетные циклы. Один цикл включает в себя фазу нагрузки, разгрузки и нагрузки с обратным знаком до того же амплитудного значения.

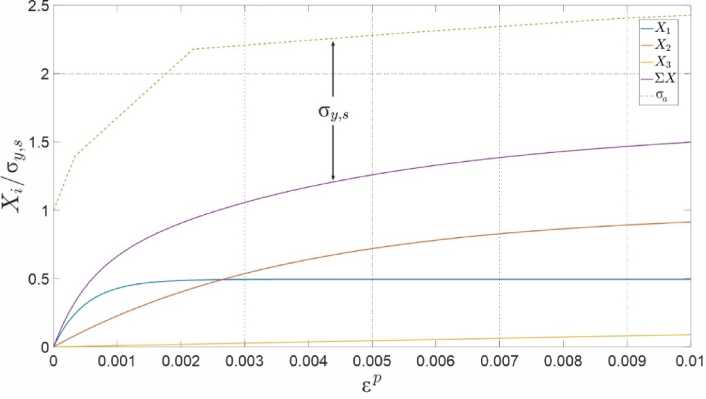
Рис. 3. Составляющая обратных напряжений в общей кривой деформирования

Fig. 3. Back stresses and material stress-strain curve

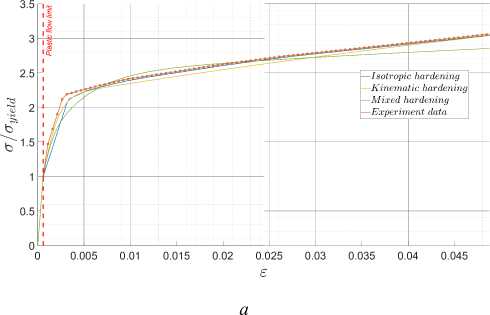
Рис. 4. Одноосное растяжение образца: а – полные кривые деформирования; b – детальное изображение в зоне перехода в пластичность

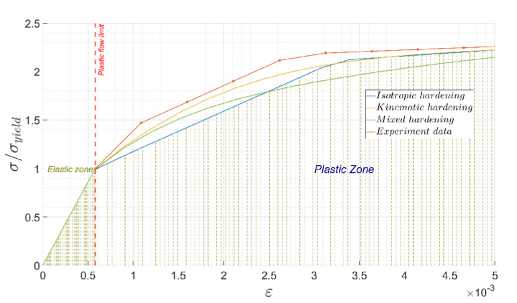
b

Fig. 4. One dimension tension: a – full stress-strain curves; b – detailed zone of plasticity initiation

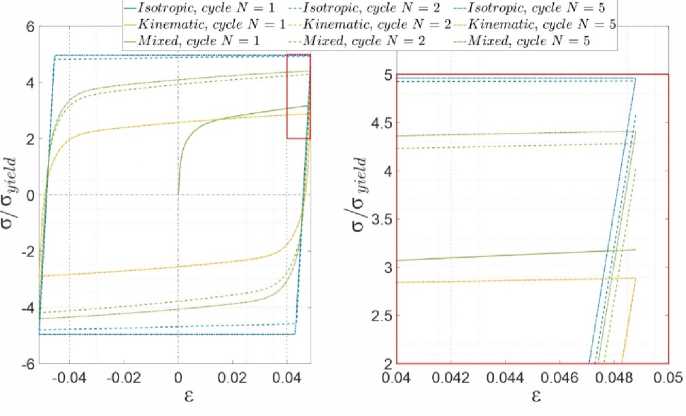
Рис. 5. Диаграммы деформирования, циклическое нагружение

• Fig. 5.    Cyclic strain-stress curves

Результаты показывают известную особенность работы различных механизмов упрочнения:

• •    изотропное упрочнение цикл за циклом увеличивает ширину гистерезисной кривой, которая равна удвоенному значению текущего предела текучести. Данный рост будет продолжаться бесконечно, если модель материала не подразумевает наличие точки разрушения образца;

• •    кинематическое упрочнение во время всего циклического нагружения не меняет ширину гистерезисной кривой, смещение центра поверхности текучести в пространстве напряжений происходит на первом цикле и больше не меняется;

• •    смешанное упрочнение содержит в себе особенности каждого из механизмов – составляющая изотропного упрочнения позволяет учитывать увеличение размера поверхности текучести, за счет чего возрастает ширина гистерезисной кривой, а составляющая кинематического упрочнения не позволяет имеет бесконечный рост данной кривой (в системе присутствует напряжение насыщения, saturated stress ).

Влияние механизма упрочнения на характер приспособляемости сосуда под давлением

Классические работы по оценке приспособляемости сосуда под давлением [5; 22–31] построены в основном на модели идеальной пластичности для получения аналитических зависимостей. Выделяются серии работ исследователей из университета Мичиган [32; 33], которые рассматривают задачу приспособляемости сосуда под давлением в условиях нелинейной диаграммы деформирования материала с учетом упрочнения. Работа [32] посвящена исследованию влияния моделей описания кинематического упрочнения на общую приспособляемость сосуда, работа [33] – процедуре оценки приспособляе- мости сосуда с учетом нелинейной упрочняющейся модели материала. Однако в данных работах не представлено исследование для смешанного механизма.

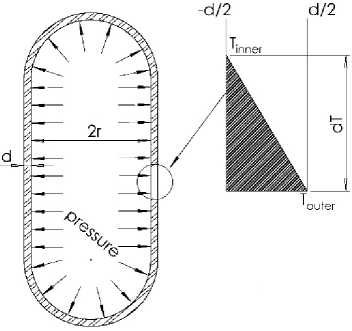
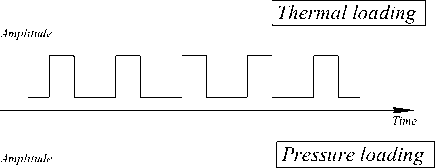
Базовые аспекты задачи оценки приспособляемости представлены в работах [5] и [34]. В последней из них описан процесс верификации автоматизированной процедуры на базе программного средства Abaqus , которая позволяет строить диаграммы Бри для сосуда под давлением при варьировании различных параметров. Для представляемого в данной работе исследования в процедуру вносятся параметры материала, описанные ранее, с целью анализа влияния механизма упрочнения на общую приспособляемость сосуда. Постановка задачи представлена на рис. 6: рассматривается сосуд под постоянным внутренним давлением, нагруженный циклически меняющимся градиентом температуры по толщине стенки.

Классическая диаграмма Бри для оригинальной задачи [5] представлена на рис. 7. Данная диаграмма получена в условиях идеально пластичного материала без упрочнения под действием описанных ранее нагрузок [34].

Линиями на диаграмме нанесено аналитическое решение для границ зон характерной приспособляемости из [5]. На дальнейших диаграммах данные линии также будут отражены для отслеживания эволюции исходной диаграммы при наличии упрочнения. Каждая из зон определяет свое характерное поведение материала [34]:

• •    зона E соответствует полностью упругому состоянию конструкции;

• •    в зонах S ₁, S ₂ – приспособляемость, упругая приспособляемость, приработка ( elastic или strict shakedown ). Такое поведение материала выражается в возникновении пластической деформации на первом цикле теплового нагружения и ее дальнейшей неизменности на протяжении жизненного цикла конструкции;

  
  
  
  
  
  

  Time

  
  

Рис. 6. Постановка задачи оценки приспособляемости

• Fig. 6.    Ratcheting test problem statement

  

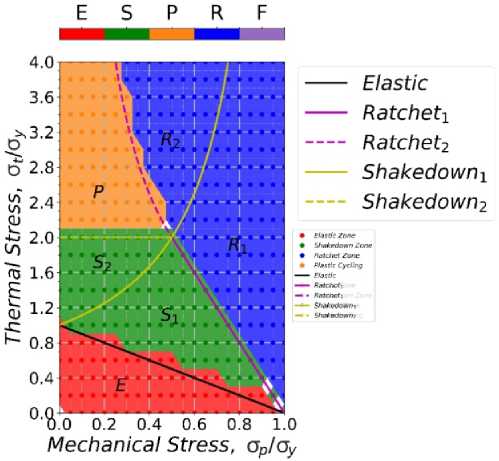
  Рис. 7. Классическая диаграмма Бри

  
  

• Fig. 7.    Bree diagram

• •    в зоне P – знакопеременная пластичность, знакопеременное неупругое деформирование ( plastic cycling или global shakedown ), для которых характерно циклическое изменение пластической деформации в процессе расчета вокруг некоторого среднего значения, которое остается неизменным. Приращение пластической деформации от цикла к циклу отсутствует;

• •    в зонах R ₁, R ₂ – рэтчетинг, непрекращающееся знакопеременное течение, прогрессирующая деформация ( ratcheting ) – неограниченный рост пластических деформаций под действием циклических нагрузок (от цикла к циклу существует ненулевое приращение пластической деформации).

Важно отметить, что для упругоидеального пластического материала диаграмма Бри имеет одинаковый вид для любого количества циклов нагружения. Очевидно, что при наличии упрочнения в материале значительный эффект на результирующую диаграмму будет оказывать количество циклов нагружения: многоцикловое упрочнение материала может приводить к стабилизации циклического поведения и «остановке» изменения диаграммы приспособляемости.

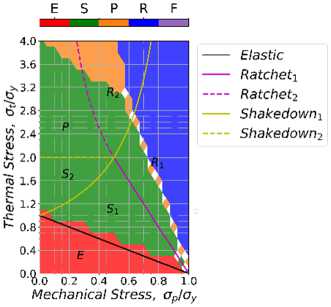
На рис. 8 представлены решения задачи для изотропного механизма упрочнения. Используется та же диаграмма деформирования материала, описание которой представлено в предыдущем разделе.

Как видно, для изотропного упрочнения характерен постепенный переход в зону приработки во всех точках диаграммы, что говорит о постепенном увеличении размера поверхности текучести, что для определенных амплитуд нагружения уже не дает прироста пластической деформации.

На рис. 9 представлены решения задачи для кинематического механизма упрочнения.

Видно, что в случае кинематического упрочнения в зону приработки переходит лишь часть диаграммы на уровне a t /а y = 2 . При этом выше данного значения часть области рэтчетинга переходит в состояние знакопеременной пластичности. Данный результат хорошо коррелирует с исследованием [32].

На рис. 10 представлены решения задачи для смешанного механизма упрочнения.

Видно, что результаты для смешанного механизма упрочнения аналогичны кинематическому механизму. Данный эффект становится понятен, если обратиться к рис. 5. Для обоих механизмов процесс упрочнения схож:

• •    на первом цикле материал получил некоторую величину упрочнения;

• •    на втором цикле при кинематическом механизме упрочнения деформация идет по той же кривой деформирования, что для первого цикла, а при смешанном – по слегка измененной «упрочненной» кривой, однако различие между этими двумя кривыми незначительно для отражения данного эффекта на диаграмме приспособляемости.

Помимо характера распределения зон приспособляемости значительное влияние на общее состояние материала оказывает абсолютная величина деформаций, возникающих в материале. На рис. 11 и 12 представлены диаграммы величин пластической деформации и приращения пластической деформации для двух механизмов упрочнения (при изначальной величине параметра b = 5,76).

а

b

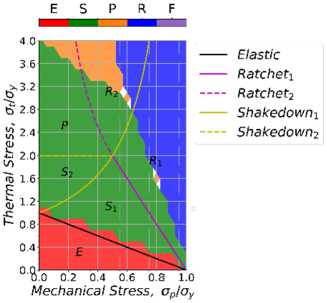
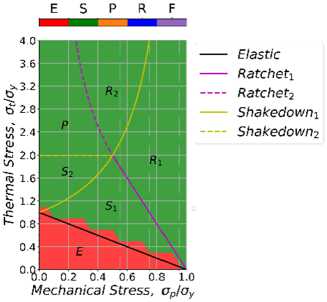
Рис. 8. Диаграммы Бри для изотропного упрочнения: a – 1-й цикл; b – 3-й цикл; c – 15-й цикл

Fig. 8. Bree diagram with isotropic hardening: a – 1^st cycle; b – 3^rd cycle; с – 15^th cycle

c

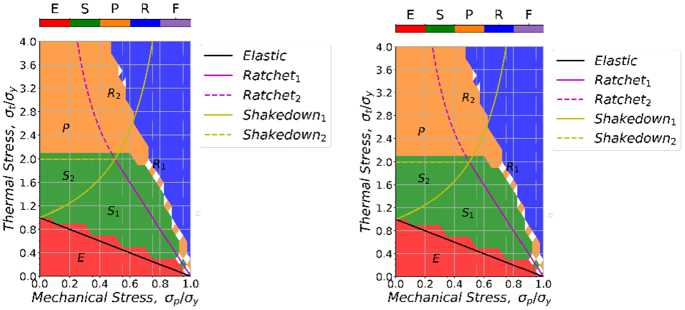
а                                           b                                          c

Рис. 9. Диаграммы Бри для кинематического упрочнения: a – 1-й цикл; b – 3-й цикл; c – 15-й цикл

Fig. 9. Bree diagram with kinematic hardening: a – 1^st cycle; b – 3^rd cycle; с – 15^th cycle

---- Elastic

---- Ratchet!

---- Ratchet2

Shakedown!

Shakedown2

а

b

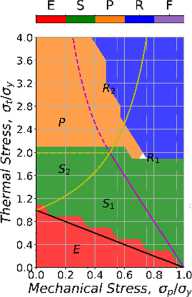
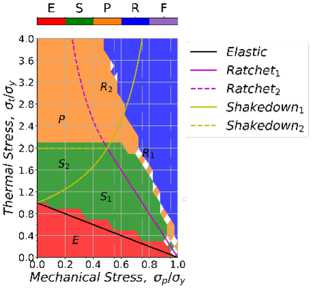
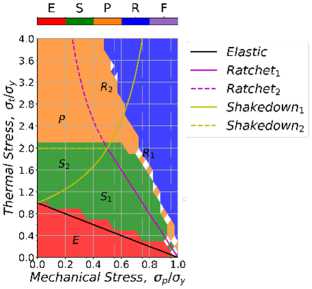
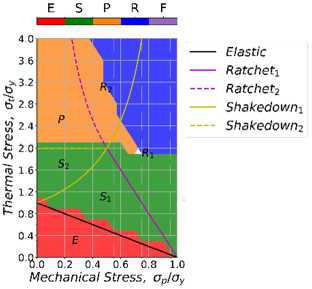
Рис. 10. Диаграммы Бри для смешанного упрочнения: a – 1-й цикл; b – 3-й цикл; c – 15-й цикл

c

Fig. 10. Bree diagram with mixed hardening: a – 1^st cycle; b – 3^rd cycle; с – 15^th cycle

а

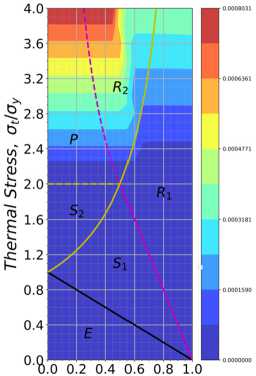
Mechanical Stress, op/oy b

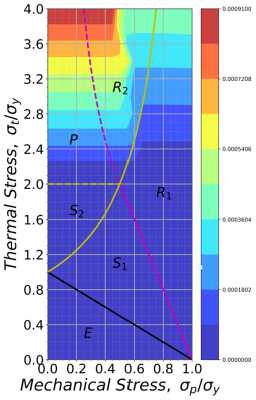
Рис. 11. Значение максимальной по толщине средней пластической деформации между циклами: а – кинематическое упрочнение; b – смешанное упрочнение

• Fig. 11.    Maximum mean plastic strains between cycles: a – kinematic hardening; b – mixed hardening

  

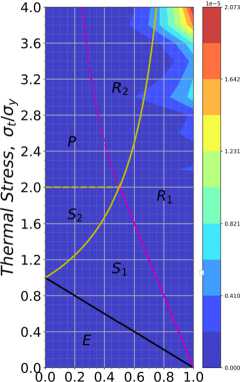
  Mechanical Stress, o_plo_y

  а

  
  
  

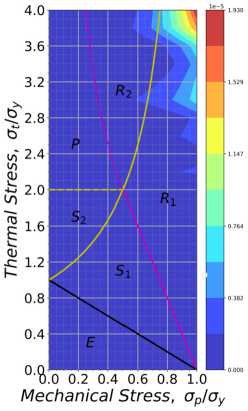
  b

  
  

Рис. 12. Значение приращения пластической деформации между циклами: а – кинематическое упрочнение; b – смешанное упрочнение

• Fig. 12.    Plastic strain increment between cycles: a – kinematic hardening; b – mixed hardening

По диаграммам видно, что значение средней деформаций и приращения между двумя последними циклами нагружения имеют различие в абсолютных значениях: кинематический механизм упрочнения дает значение деформаций на 12 % выше, чем смешанный механизм, за счет отсутствия составляющей изотропного упрочнения, повышающего прочностные характеристики материала.

Заключение

Согласно российским и зарубежным нормам проектирования атомных станций, оценка прочности оборудования и реакторных установок в условиях циклических нагрузок с учетом неупругого поведения материала должна включать в себя как отсутствие неограниченного роста пластических деформаций (отсутствие рэтче-тинга), так и непревышение допустимых значений по общим накопленным деформациям. Данные требования предъявляются для полномасштабных расчетов с заданием циклических нагрузок на весь жизненный цикл и последовательным моделированием каждого цикла нагружения. Подобные расчеты применяются в случаях, когда упрощенные консервативные методики оценки